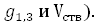Способы определения запаса древостоев
Формульные, табличные, вычислительные и графические
Академик Н.П. Анучин (1982), отстаивая необходимость унифицировать методы учета древесины и выработки единых нормативов, отмечает, что: «Этот принцип обобщений не должен игнорировать биологических особенностей отдельных пород, различий в динамике их роста и специфических особенностей среды и условий местопроизрастания». Им разработаны формульные методы определения общего запаса древостоя на основе измерения абсолютной полноты и средней высоты для светолюбивых и теневыносливых пород.
В.В. Загреев (1992) предложил следующие простейшие формулы для определения запаса древостоя элемента леса:
для сосны, лиственницы, дуба, осины, липы, граба
| M = ΣG ( Ν + 3 ) 0,40, | (87) |
| ели, пихты, бука, ольхи | |
| М = ΣG ( Н + 2 ) 0,44, | (88) |
| березы | |
| М = ΣG ( Н + 2,6 ) 0,39, | (89) |
где ΣG – сумма площадей поперечных сечений стволов на 1 га (абсолютная полнота), м 2 ;
Н – средняя высота древостоя элемента леса , м.
По Н.В. Третьякову, общая формула определения запаса имеет вид
| М = К ( Н – а )·Р, | (90) |
где К и а – коэффициенты, зависящие от древесной породы;
Р – относительная полнота.
, (91)
 |  | |
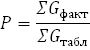
где ΣGфакт – абсолютная полнота древостоя, определяемая в лесу с помощью полнотомеров разных систем;
ΣGтабл – абсолютная полнота, взятая из таблиц при полноте 1,0 при соответствующей средней высоте. Формулы Н.В. Третьякова для конкретных древесных пород следующие:
| для сосны | |
| М = 17,5× ( Н — 2 ) × Р, | (92) |
| ели | |
| М = 23,3× ( Н — 6 ) × Р, | (93) |
| березы | |
| М = 17,5× ( Н — 6 ) × Р, | (94) |
| осины | |
| М = 22,5× ( Н — 7 ) × Р. | (95) |
Запас смешанного древостоя можно определить как сумму запасов составляющих его пород:
где М1 и М2 – запасы составляющих пород при полноте 1,0;
Р1 и Р2 – относительные полноты составляющих пород.
При отсутствии данных об относительных полнотах составляющих пород запас можно определить по формуле
| М = ( М1 К1 + М2 К2 ) × Робщ, | (97) |
где К1 и К2 – доли участия пород в составе древостоя;
Робщ – общая относительная полнота древостоя.
Табличные способы прицельно-измерительной таксации древостоев, как и при помощи формул, основаны на измерении полноты (абсолютной или относительной) и средней высоты древостоя элемента леса. Относительная полнота определяется по таблицам хода роста нормальных насаждений или по «стандартной» таблице сумм площадей сечений и запасов при полноте 1,0.
Критериям полноты в сосновых насаждениях посвящена работа А.В. Вагина (1976). Он отмечает, что все подобные таблицы не учитывают при равных высотах древостоев влияние на сумму площадей сечений класса бонитета насаждений. Между тем с ухудшением условий местопроизрастания при одинаковых высотах насаждений их суммы площадей сечений уменьшаются. Работами ВНИИЛМ (В.В. Загреев, Н.В. Выводцев, В.С. Чернявский, В.П. Закутин, Н.Я. Саликов и др.) также установлена зависимость сумм площадей сечений нормальных древостоев основных лесообразующих пород от классов бонитета. По данным этих авторов, введение класса бонитета как дополнительного входа в таблицы позволяет придать им универсальность (пригодны для применения во всех районах страны) и повысить точность таксации относительных полнот и запасов за счет приведения эталонов нормальной полноты в соответствие с условиями местопроизрастания. Сведения даются по кедру, ильму и ясеню – Н.В.Третьяковым, по дубу – А.Д. Дударевым, по ольхе черной – общими таблицами хода роста, по липе – П.А. Соколовым.
 | |
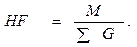
Второй табличный способ прицельно-измерительной таксации запаса древостоя основан на применении так называемой «видовой высоты» (HF)
где HF — видовая высота в м 3 , приходящаяся на 1 м 2 суммы площадей поперечных сечений стволов древостоя:
По исследованиям Эйнгорна, Воропанова, Загреева, Верхунова, видовая высота (HF) зависит от класса бонитета насаждений. С ухудшением условий местопроизрастания видовая высота (HF) возрастает. Влияет на величину HF также происхождение насаждений.
В лесоустроительной практике запас древостоя находится по таблице сумм площадей сечений и запасов при полноте 1,0 или местным таблицам хода роста (ТХР).
Вычислительные способы определения запаса леса основаны на рубке модельных и учетных деревьев в древостое. Запас древостоя представляет собой сумму объёмов составляющих стволов, которую можно получить умножением объема среднего дерева на число стволов. Такое дерево называют теоретическим модельным деревом древостоя. Дерево, срубленное в качестве среднего, но отличающееся от него по своим таксационным показателям, называется действительным модельным деревом древостоя.
Площадь сечения теоретической модели:
отсюда 
. (99)
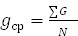
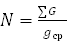
Поскольку объемы стволов изменяются пропорционально площади сечений, то в случаях несовпадения показателей теоретических и действительных моделей вычисляют скрытое число стволов древостоя (N1):
и 
. (100)
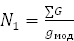
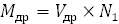
Модельные деревья берутся как средние для своего древостоя или по ступени толщины древостоя. В последнем случае каждая ступень толщины рассматривается как отдельный древостой. Ошибка при рубке лишь одной средней модели древостоя может составлять ± 18-22%, поскольку сложно определить форму ствола. По данным профессора Дворецкого, точность способа модельных деревьев по ступени толщины зависит от числа отобранных деревьев. Модельные деревья по ступени толщины отбираются независимо или пропорционально числу деревьев.
Расчет запаса при взятии учетных деревьев. Определение запаса проводят по таксируемым совокупностям деревьев (ступень толщины древостоя).
Достоинством способа является простота отбора деревьев в натуре, возможность расчета необходимого числа деревьев для достижения заданной точности работ. При одном и том же количестве отобранных деревьев проценты ошибок по учетным деревьям в 1,4 раза больше, чем по модельным деревьям.
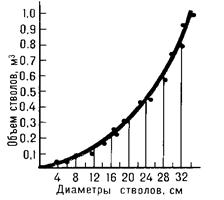
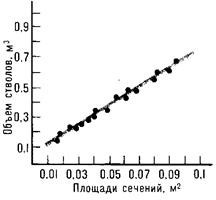
Графические способы определения запаса древостоя основаны на наличии тесной связи между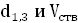 
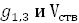
(кривая объемов), а также тесной связи между 
(прямая объемов)(рисунок 6).
Рисунок 6– кривая (а) и прямая (б) объёмов ствола
Число деревьев должно быть не менее 10-12 шт. 
Точность способов кривой объёмов ± 3%, а прямой объёмов ±2-3%.
Достоинства графических способов – это свобода выбора деревьев, возможность контроля удачности взятия моделей, наглядность и простота работ. Основной недостаток способа – это некоторая неопределенность и субъективность построения графиков. Данный недостаток легко устраняется математическим моделированием и построением уравнений связи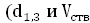 
;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Таксационные закономерности совокупностей элементов леса
Классификация способов определения запаса древостоя
Способы определения запаса древостоя
Формульные, табличные, вычислительные и графические
Таксационные закономерности совокупностей элементов леса
Классификация способов определения запаса древостоя
Таксация запаса древостоев
Лекция 9
Определение запаса древостоя в зависимости от целей ведения хозяйства может проводиться с разной точностью, с применением различных методов оценки леса.
Практика лесного хозяйства имеет дело как с отдельным древостоем, так и с совокупностью древостоев элементов леса в определённых хозяйственных секциях, объеденных однородностью режима ведения и целей хозяйства. Для выявления запаса леса в этих секциях образуют так называемые страты – это качественно однородные группы древостоев по породе, среднему коэффициенту формы, разряду высот и типу возрастной структуры.
Основой методов учета запаса древостоя являются закономерности строения древостоя и совокупностей элементов леса.
Способы определения запаса древостоя подразделяются на следующие группы:
1) Прицельно-измерительные способы:
— визуальное определение запаса леса;
— измерение суммы площадей сечения древостоя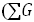 
) и средней высоты древостоя (Нср) с применением специальных формул или таблиц;
— определение относительной полноты (Р) и средней высоты древостоя (Нср), среднего возраста (Аср), класса бонитета с применением стандартных таблиц сумм площадей сечений и запасов при полноте 1,0 или по таблицам хода роста (ТХР) нормальных насаждений;
— аналитико-измерительное дешифрирование аэрофотоснимков.
2) Перечислительные способы:
а) по охвату объектов:
— со сплошным перечетом деревьев на участке;
— с частичным перечетом деревьев на заложенных пробных площадях;
б) по способу обработки данных:
в) по способу определения средних объемов стволов:
— с рубкой деревьев;
— с использованием таблиц объемов стволов;
г) по способу отбора срубаемых деревьев:
— по модельным деревьям, средним по диаметру, высоте, видовому числу (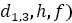
для соответствующих групп стволов;
— по учетным деревьям, отбираемым статистическим методом.
Объединяющей категорией для таксационных совокупностей элементов леса выступает разряд высот, определяемый по соотношению средних диаметров и высот древостоя данной породы.
Разряды высот передают соотношения диаметров и высот деревьев в древостое. Отличаются один от другого тем, что при одних и тех же диаметрах их высоты и объемы тем больше, чем меньше номер разряда. В таком же порядке изменяется средний сбег стволов: низшие разряды – наиболее сбежистые, высшие – наиболее полнодревесные. Выпуклые линии, характеризующие изменение средних высот стволов, по ступени толщины представляют на графике веер, расходящийся от начала координат. Внизу находятся линии низших разрядов, вверху – высших.
Разряды высот древостоя устанавливаются только по соотношению диаметра и высоты (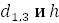
) деревьев, независимо от среднего возраста (Аср), относительной полноты (Р), классов бонитета и условий местопроизрастания.
В совокупностях древостоев элементов леса по разрядам высот проявляются следующие таксационные закономерности:
1. Профессор А.В. Тюрин выявил, что в древостоях имеющих одинаковые средние высоты и диаметры наблюдается одинаковое соотношение высот и диаметров деревьев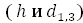
, независимо от возраста и класса бонитета насаждений, но с учётом одного лесорастительного района.
2. Профессор Н.В. Третьяков выявил, что древостои, средние деревья которых имеют одинаковые диаметры, высоты и вторые коэффициенты формы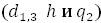 
, характеризуются одинаковыми объёмами (Vср), независимо от возраста, полноты, класса бонитета и других признаков леса.
3. Совокупности элементов леса в стратах обладают значительно большим диапазоном изменчивости таксационных показателей деревьев, чем в отдельном древостое. Коэффициент изменчивости их здесь выше в 1,5-1,8 раза. Однако здесь сохраняются закономерности строения по таксационным показателям, присущие отдельным древостоям.
4. Закономерности взаимосвязей таксационных показателей деревьев по разрядам высот используются при составлении объемных и сортиментных таблиц.
5. Закономерности изменения процента выхода древесины и сортиментов от диаметра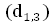 
используются при составлении сортиментных таблиц.
6. Закономерности распределения процента общего числа деревьев и деловых стволов по относительным ступеням толщины используются при разработке методов учета товарной структуры леса, составления товарных таблиц.
7. Закономерные соотношения средних значений приростов по таксационным показателям древостоя от значений самих таксационных показателей используются при разработке методов учета прироста запаса древостоев.
8. Закономерности изменения средних таксационных показателей древостоя в стратах, выраженных в виде естественных рядов развития насаждений с возрастом, используются при составлении таблиц хода роста (ТХР) насаждений.
Из таксационных закономерностей, проявляющихся в отдельных древостоях элементов леса, при определении запаса можно использовать следующие:
1) закономерности строения древостоя элемента леса по таксационных показателям;
2) зависимость редукционных чисел таксационных показателей от ранга деревьев;
3) зависимости коэффициента изменчивости таксационных показателей от природных факторов;
4) связь между редукционными числами диаметра и остальными таксационными показателями;
5) важнейшие взаимосвязи таксационных показателей в древостое между собой.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
