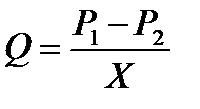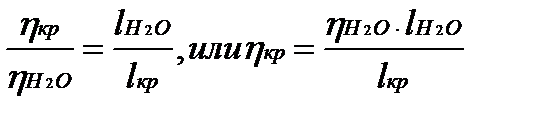Медицинская вискозиметрия. Принцип работы медицинского вискозиметра
Вязкость (внутреннее трение) жидкости — свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой. Движение реальной жидкости при малых скоростях носит слоистый (ламинарный) характер. При установившемся ламинарном течении бесконечно малые слои жидкости скользят относительно друг друга, не перемешиваясь, и сохраняют во времени свои пространственные положения. При возрастании различия в скоростях соприкасающихся слоёв, силы трения между ними также возрастают. Это приводит к тому, что при некоторой критической величине скоростей, разной для разных жидкостей, характер течения существенно меняется. Возникает энергичное перемешивание слоёв жидкости. Положение слоёв в пространстве с течением времени постоянно меняется, появляются вихри. Такое движение называется турбулентным. Важным свойством турбулентного течения (в сравнении с ламинарным) является высокое сопротивление потоку.
Гидравлическое сопротивление
Чтобы изучить явление гидравлического сопротивления, используем формулу Пуазейля. С учётом объёмного потока жидкости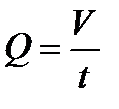 
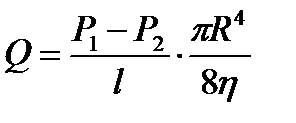
, протекающей через горизонтальную трубу за 1с, формула Пуазейля принимает следующий вид: 
, где Р1— давление в начале изучаемого участка трубы, Р2 — давление в конце этого участка, l — длина изучаемого участка трубы, η — динамическая вязкость жидкости, протекающей по трубе.
Здесь величина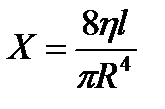 
— это гидравлическое сопротивление, как видно оно зависит от радиуса трубы (R), длины участка трубы (l) и вязкости жидкости (η). Гидравлическое сопротивление тем больше, чем больше вязкость и длина трубы и чем меньше площадь поперечного сечения.
Формулу для объёмного потока жидкости можно записать так: 
Число Рейнольдса
Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы. Английский физик и инженер Осборн Рейнольдс (1842-1912) изучал переход от ламинарной формы течения к турбулентной. Он экспериментально показал, что турбулентность возникает, когда определенная комбинация величин, характеризующих движение, превосходит некоторое критическое значение. Им было введено безразмерное число, позднее названное в его честь числом Рейнольдса, которое характеризует течение жидкости по трубе (каналу).Число Рейнольдса определяется по формуле: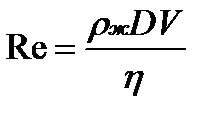 
, где ρж — плотность жидкости, η — ее вязкость, V — скорость течения, D — диаметр трубы. Это число является критерием вида течения. Существует критическое значение числа Рейнольдса: для гладких цилиндрических труб ReKp = 2300. Если число Рейнольдса больше критического, то движение жидкости турбулентное, если меньше, то ламинарное. Например, при атеросклерозе критическое число Рейнольдса в некоторых сосудах становится равным 1160.
Так как число Рейнольдса зависит от вязкости и плотности жидкости, то удобно использовать в этой формуле кинематическую вязкость: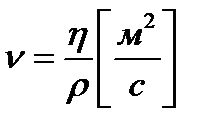 
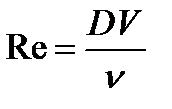
. Тогда число Рейнольдса можно записать в виде 
. Число Рейнольдса является критерием подобия. При моделировании гидро- и аэродинамических систем, в частности кровеносной системы, модель должна иметь такое же число Рейнольдса, как и сам объект, в противном случае не будет соответствия между ними.
Кинематическая вязкость полнее, чем динамическая, учитывает влияние внутреннего трения на характер течения жидкости или газа. Так, динамическая вязкость воды приблизительно в 100 раз больше, чем воздуха (при 0°С), но кинематическая вязкость воды в 10 раз меньше, чем воздуха, и поэтому кинематическая вязкость сильнее влияет на характер течения воздуха, чем воды.
Характер течения жидкости или газа существенно зависит от размеров трубы. В широких трубах даже при сравнительно небольших скоростях может возникнуть турбулентное движение. Так, например, в трубке диаметром 2 мм течение воды становится турбулентным при скорости более 127 см/с, а в трубе диаметром 2 см — уже при скорости примерно 12 см/с (температура . 16°С). Течение крови по такой трубе стало бы турбулентным при скорости 50 см/с, но практически в кровеносных сосудах диаметром 2 см турбулентное течение возникает даже при меньшей скорости.
Течение крови в артериях в норме является ламинарным, небольшая турбулентность возникает вблизи клапанов. При патологии, когда вязкость бывает меньше нормы, число Рейнольдса может превышать критическое значение и движение станет турбулентным. Турбулентное течение связано с дополнительной затратой энергии при движении жидкости, что в случае крови приводит к добавочной работе сердца.
Шум, возникающий при турбулентном течении крови, может быть использован для диагностирования заболеваний. Этот шум прослушивают на плечевой артерии при измерении давления крови методом звуков Короткова. Течение воздуха в носовой полости в норме ламинарное. Однако при воспалении или каких-либо других отклонениях от нормы оно может стать турбулентным, что повлечет дополнительную работу дыхательных мышц.
Переход от ламинарной формы течения к турбулентной происходит не только при течении в трубе (канале), он характерен почти для всех течений вязкой жидкости. В частности, обтекание жидкостью профиля корабля или подводной лодки, тела рыбы или крыла самолета или птицы также характеризуется ламинарно-турбулентным переходом, при этом в формулу нужно подставить характерный размер обтекаемого тела и константу, зависящую от формы тела.
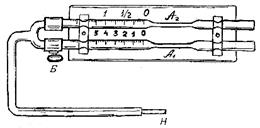
Медицинский вискозиметр (вискозиметр Гесса) используется для определения вязкости крови. Принцип его действия основан на том, что скорости продвижения жидкостей в капиллярах с одинаковыми сечениями при равных температурах и давлениях зависят от вязкости этих жидкостей.
Из формулы Пуазейля следует, что объемы жидкостей, протекающих за равные промежутки времени по одинаковым капиллярам, обратно пропорциональны вязкостям этих жидкостей. Следовательно,
.
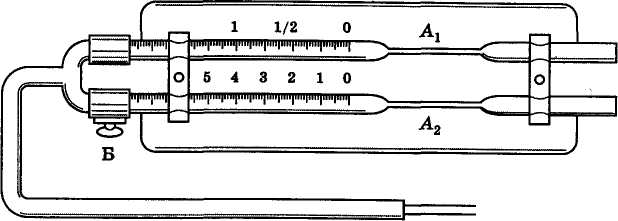
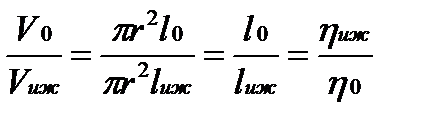
Медицинский вискозиметр состоит из двух одинаковых градуированных
капилляров А1 и А2 . В капилляр А2 набирают определенный объем
дистиллированной воды и перекрывают кран Б. Это позволяет
набрать в капилляр А1 исследуемую жидкость, не изменяя уровень воды. Если
теперь, открыв кран Б, создать разрежение в вискозиметре, то перемещения
жидкостей за одно и то же время будут обратно пропорциональны их вязкости
где ηкр — вязкость крови; ηН2О — вязкость воды. Если вязкость воды принять равной единице, а путь, пройденный кровью, составляет одно деление вискозиметра, то на основании формулы относительная вязкость крови численно равна пути lН2О, пройденному при этом водой.
Вязкость крови человека в норме 4 — 5 мПа·с, при патологии колеблется от 1,7 — 22,9 мПа·с, что сказывается на скорости оседания эритроцитов (СОЭ). Венозная кровь обладает несколько большей вязкостью, чем артериальная. При тяжелой физической работе увеличивается вязкость крови. Некоторые инфекционные заболевания увеличивают вязкость, другие же, например брюшной тиф и туберкулез, — уменьшают.
Источник
Тема: ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ МЕТОДАМИ ОСВАЛЬДА, ГЕССА И СТОКСА
ЦЕЛЬ РАБОТЫ:изучить понятие вязкости и основные методы определения вязкости; ознакомиться с работой медицинского вискозиметра и вискозиметра Освальда; определить вязкость исследуемой жидкости медицинским вискозиметром и вискозиметром Освальда.
ПРИБОРЫИ ПРИНАДЛЕЖНОСТИ:вискозиметр Освальда, вискозиметр Гесса, вискозиметр Стокса, секундомер, дистиллированная вода, исследуемые жидкости, химическая посуда.
При течении реальной жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называют внутренним трениемиливязкостью.
Все жидкости по вязкости подразделяют на ньютоновские и неньютоновские. Жидкости, которые подчиняются уравнению Ньютона (1) называют ньютоновскими, а их вязкость нормальной. Неньютоновские жидкости не подчиняются уравнению Ньютона и их вязкость называют аномальной.
(1)
где η – коэффициент пропорциональности или динамическая вязкость; 
— градиент скорости, S – площадь взаимодействующих слоев.
Единицей вязкости является паскаль-секунда (Па·с).
Вязкость зависит от состояния и молекулярных свойств жидкости. Для ньютоновских жидкостей вязкость не зависит от градиента скорости, а у неньютоновских — зависит. Неньютоновские жидкости состоят из сложных и крупных молекул, их вязкость при одинаковых условиях много больше ньютоновских.
Совокупность методов измерения вязкости называют вискозиметрией, а приборы, используемые для этих целей, – вискозиметрами.Существуют несколько наиболее распространенных методов определения вязкости жидкости: капиллярный и метод падающего шарика (Стокса).
1.Капиллярный метод основан на формуле Пуазейля и заключается в измерении времени протекания определенного объема жидкости через вертикальный капилляр. Для протекания жидкости или газа через трубку требуется некоторая разность давления. Зависимость между объемом V жидкости (газа), протекающей за время t через трубку длиной l, и разностью давленийDP на концах трубки выражается формулой Пуазейля
V=pr 4 D Pt/8hl (2)
где r — радиус трубки, h — динамическая вязкость жидкости или газа.
Для определения вязкости по формуле (2) необходимо, чтобы течение было ламинарным, т.е. таким, при котором слои жидкости (газа) текут, не перемешиваясь. Для вихревого (турбулентного) течения формула Пуазейля несправедлива. Чтобы при обычных скоростях вихри не появились, трубка должна быть достаточно тонкой.
Более полно характер течения вязкой жидкости определяется кинематической вязкостью n:
где r — плотность жидкости.
Капиллярные вискозиметры бывают самой различной формы. Ими измеряют вязкость от значений 10 -5 Па·с, свойственных газам, до значений 10 4 Па·с, характерных для консистентных смазок. Для определения вязкости крови
(4-5·10 -3 Па·с) чаще всего используют именно капиллярные вискозиметры.
Измерение входящих в формулу Пуазейля величин r, .l и DP провести трудно, поэтому прибегают к определению вязкости жидкости методом сравнения её движения в данном вискозиметре с движением эталонной жидкости, вязкость которой известна, например, воды.
Капиллярный вискозиметр Освальда изображен на рис.1. Одно колено вискозиметра представляет собой капиллярную трубку. Определённый объем воды вливают в широкое колено вискозиметра, а затем с помощью груши поднимают уровень воды в узком колене так, чтобы он поднялся чуть выше отметки А.
 Рис. 1 | Сняв грушу, наблюдают за понижением этого уровня. Когда мениск проходит метку А, включают секундомер, а при прохождении метки В — выключают. Так находят время прохождения воды между метками А и В. При ламинарном течении жидкости время прохождения этого объема через капилляр длиной l будет таким же. Так же определяют время t протекания исследуемой жидкости между метками А и В. |
Объём исследуемой жидкости берут равным объёму воды. Для равных объёмов жидкостей, протекающих через капилляр, можно записать:
V=pr 4 D Pt/8hl, — для исследуемой жидкости (4´)
Так как объемы жидкостей одинаковы, следовательно, можно приравнять правые части уравнений (4) и (4’):
Гидростатическое давление исследуемой жидкости в капилляре равно
где r — плотность жидкости, h — разность уровней жидкости в двух коленах вискозиметра.
Соответственно, для воды с учетом уравнения (6):
Подставляя (6) и (7) в уравнение (5), получаем
С учетом (3) уравнение (8) принимает вид:
где n — кинематическая вязкость исследуемой жидкости, n0 — кинематическая вязкость воды,t — время истечения исследуемой жидкости, t0 — время истечения воды.
Обозначим постоянную прибора
Тогда формула (9) примет вид
Медицинский вискозиметр (рис. 2) используется для определения вязкости крови. Принцип его действия основан на том, что скорости продвижения жидкости в капиллярах с одинаковыми сечениями при равных температурах и давлениях зависят только от вязкостей этих жидкостей.
Из формулы Пуазейля следует, что объем жидкостей, протекающих за равные промежутки времени по одинаковым капиллярам, обратно пропорционально вязкостям этих жидкостей. Следовательно,
Медицинский вискозиметр состоит из двух одинаковых градуированных капилляров А1 и А2 (Рис. 2). В капиллярах А1 набирают определенный объем дистиллированной воды и перекрывают кран Б. Это позволяет набрать в капилляр А исследуемую жидкость, не изменяя уровень воды. Если теперь открыть кран Б, создать разряжение в вискозиметре, то перемещение жидкостей за одно и то же время будет обратно пропорционально их вязкости:
где h — вязкость исследуемой жидкости, ho — вязкость воды. Если вязкость воды принять равной единице, а путь, пройденный жидкостью, составляет одно деление вискозиметра, то на основании (12) вязкость жидкости будет численно равна пути, пройденному при этом водой.
2.Метод падающего шарика.
Вязкость проявляется при движении не только жидкости по сосудам, но и тел в жидкости. При небольших скоростях в соответствии с уравнением Ньютона сила сопротивления движущемуся телу пропорциональна вязкости жидкости, скорости движения тела и зависит от размеров тела.
Для сферического тела (шарик) зависимость силы сопротивления при его движении в сосуде с жидкостью от перечисленных выше факторов выражается формулой Стокса:
где r –радиус шарика; υ – скорость его падения. Этот закон получен в предположении, что стенки сосуда не влияют на движение шарика.
При падении шарика в вязкой среде на него действуют три силы: сила тяжести, выталкивающая (архимедова) сила, равная весу вытесненной шариком жидкости, исила сопротивления, вычисляемая по формуле Стокса (рис.3).
 Рис. 3 | Когда все эти силы уравновесятся, то, согласно первому закону Ньютона, шарик начинает падать с постоянной скоростью. Определив эту скорость и задав параметры шарика и жидкости, можно определить силу сопротивления падению шарика в вязкой среде. По этой же формуле можно определить и вязкость жидкости, если известна сила сопротивления, которую можно определить из условия равенства нулю равнодействующей всех вышеназванных сил. |
Этот метод часто используется для определения вязкости жидкостей. Предел измерений коэффициента вязкости вискозиметрами с падающим шариком составляет 6·10 4 ÷ 250 Па·с.
I.Определение кинематической вязкости жидкости методом Освальда:
1. Отмерить с помощью мерного стакана исследуемой жидкости в количестве 10 мл и залить его в широкое колено вискозиметра (см. рис. 1).
2. С помощью груши поднять уровень жидкости во втором колене выше метки А.
3. Измерить время прохождения жидкости t от метки А до В при ее медленном истечении. Опыт провести не менее трех раз.
4. Вылить исследуемую жидкость и повторить опыт с контрольной жидкостью (вода).
5. Рассчитать постоянную вискозиметра по формуле:
где ν0 – кинематическая вязкость контрольной жидкости (справочные данные см. в приложении 2); t0 – время протекания контрольной жидкости.
6. Рассчитать вязкость исследуемой жидкости по формуле:
где t – время протекания исследуемой жидкости.
7. Данные занести в таблицу 1. Рассчитать абсолютную и относительную погрешность. Сравнить полученное значение вязкости со справочным, сделать вывод.
| № | t0, с | t, с | А, м 2 /с 2 | ν, м 2 /с | Δν, м 2 /с | ε, % |
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| Ср.зн. |
II. Определение вязкости жидкости медицинским вискозиметром:
1. С помощью груши поднять контрольную жидкость в капиллярной трубке (1) по уровень 0. Перекрыть кран (3) (см. рис. 2).
2. В трубке (2) поднять уровень исследуемой жидкости до нулевого уровня.
3. Открыть кран и через общую трубку (4) с помощью груши создать разряжение. За одинаковый промежуток времени определить, на какой уровень поднимутся обе жидкости. Опыт повторить не менее трех раз.
4. Зная уровень поднятия обеих жидкостей, определить вязкость исследуемой жидкости η, используя формулу:
где η0 – динамическая вязкость контрольной жидкости, l0 — уровень поднятия контрольной жидкости, l – уровень поднятия исследуемой жидкости (η0 – берут из справочной таблицы).
5. Полученные данные занести в таблицу 2. Рассчитать абсолютную и относительную погрешность. Сравнить со справочными данными. Сделать вывод.
Источник
