Способы определения внутренней энергии идеального газа

Внутренняя энергия идеального газа

На этой странице вы можете рассчитать внутреннюю энергию идеального газа с помощью калькуляторов онлайн или самостоятельно по формулам.

через массу, молярную массу и температуру

Формула для нахождения внутренней энергии идеального одноатомного газа через массу, молярную массу и температуру:

<2>\cdot \dfrac \cdot R T> , где U — внутренняя энергия газа, m — масса газа, M — молярная масса газа, R — универсальная газовая постоянная R = 8,3144598(48) Дж⁄(моль∙К), T — абсолютная температура газа.

через давление и объем

Формула для нахождения внутренней энергии идеального одноатомного газа через давление и объем:

<2>\cdot p V> , где U — внутренняя энергия газа, p — давление газа, V — объем газа.

через количество вещества и температуру

Формула для нахождения внутренней энергии идеального одноатомного газа через количество вещества и температуру:

<2>\cdot \nu RT> , где U — внутренняя энергия газа, \nu — количество вещества (в молях), R — универсальная газовая постоянная R = 8,3144598(48) Дж⁄(моль∙К), T — абсолютная температура газа.

через степени свободы

Формула для нахождения внутренней энергии идеального одноатомного газа через количество вещества и температуру:

<2>\cdot \nu RT> , где U — внутренняя энергия газа, i — количество степеней свободы, \nu — количество вещества (в молях), R — универсальная газовая постоянная R = 8,3144598(48) Дж⁄(моль∙К), T — абсолютная температура газа.

Количество степеней свободы молекулы идеального газа

Число степеней свободы (i) — наименьшее число независимых координат, которое необходимо ввести, чтобы определить положение тела в пространстве.

Источник

Внутренняя энергия и работа идеального газа

теория по физике 🧲 термодинамика

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

U = ∑ E k 0 = N E k 0 = m N A M . · i k T 2 . . = i 2 . . · m M . . R T = i 2 . . ν R T = i 2 . . p V

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Изменение внутренней энергии идеального газа в изопроцессах

Δ U = 3 2 . . · m M . . R T = 3 2 . . ν R T = 3 2 . . ν R ( T 2 − T 1 )

Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p V 2 − p V 1 ) = 3 2 . . p Δ V

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p 2 V − p 1 V ) = 3 2 . . V Δ p

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p 2 V 2 − p 1 V 1 )

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

Перемещение равно разности высот поршня в конечном и начальном положении:

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A ‘ = p ( V 2 − V 1 ) = p Δ V > 0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A ‘ = p ( V 2 − V 1 ) = p Δ V 0

Работа идеального газа при нагревании газа:

A ‘ = ν R Δ T = ν R ( T 2 − T 1 ) = m M . . ν R Δ T

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изохорное охлаждение и изобарное сжатие:

Изобарное расширение: A ‘ = p ( V 2 − V 1 )
Изобарное сжатие: A ‘ = p ( V 2 − V 1 )
Изохорное охлаждение:
Замкнутый цикл: 1–2: A ‘ = ( p 1 − p 3 ) ( V 2 − V 1 )
Произвольный процесс: A ‘ = p 1 + p 2 2 . . ( V 2 − V 1 )

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A 2 = p ( V 2 − V 1 ) = 4 p ( 5 V − 3 V ) = 4 p 2 V = 8 p V

A 1 = p ( V 2 − V 1 ) = p ( 5 V − V ) = 4 p V

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1. Определить по графику, как меняется давление.
2. Определить, как меняется объем.
3. Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Источник

Внутренняя энергия идеального газа

Средняя оценка: 4.2

Всего получено оценок: 132.

Средняя оценка: 4.2

Всего получено оценок: 132.

С помощью понятия внутренней энергии в физике объясняются процессы, когда работа может совершаться покоящимся телом за счет энергии отдельных частиц, из которых состоит это тело. В большинстве случаев величина внутренней энергии тела представляет собой сумму потенциальной энергии взаимодействия молекул, составляющих тело, и кинетической энергии их хаотического теплового движения. Для описания тепловых явлений в веществах, находящихся в газообразном состоянии, используется модель идеального газа, которая позволяет получить достаточно простые формулы для величины внутренней энергии идеального газа.

Что такое идеальный газ

Газ – это агрегатное состояние вещества, для которого характерна большая подвижность его частиц (большие длины пробега) и очень слабая связь между молекулами и атомами. В газообразном состоянии вещество не имеет определенной формы и объема. Любое вещество может быть переведено в газообразное состояние с помощью подбора необходимых параметров давления и температуры.

Идеальным называется газ, имеющий следующий набор свойств:

• Молекулы имеют пренебрежимо малые размеры;
• Молекулы не взаимодействуют между собой (отсутствуют силы притяжения и отталкивания);
• Расстояния между молекулами много больше размеров молекул;
• Молекулы отталкиваются только при соударениях друг с другом и со стенками сосуда, где они находятся. Соударения описываются формулами из раздела механики для соударения шаров;
• Движение молекул происходит по законам Ньютона;
• Газ оказывает давление на стенки сосуда за счет ударов молекул газа.

Рис. 1. Модель давления идеального газа.

Определение внутренней энергии

Внутренняя энергия вещества U — это сумма потенциальной энергии взаимодействия молекул E_п, составляющих тело, и кинетической энергии их хаотического теплового движения E_k:

Для вычисления внутренней энергии газа U_г в формуле (1) можно пренебречь потенциальной составляющей энергии, то есть:

Полная кинетическая энергия вещества Е п _к получается сложением энергий всех отдельных частиц:

$ Е^п_к = Е_1 + Е_2 + Е_3 +…. Е_N $ (2),

где N — общее число частиц в газе.

Частица массой m, движущаяся со скоростью v, обладает кинетической энергии Е_к, которую можно вычислить с помощью формулы, полученной в разделе механики:

Найти полную кинетическую энергию всех частиц газа помощью формул (2) и (3), не представляется возможным — для этого необходимо знать скорости и массы всех частиц, а также их общее количество. Учитывая, что только в одном моле вещества находится гигантское число молекул (6,023*10 23 !), становится понятно, что для нахождения внутренней энергии даже такой простой системы, как идеальный газ, требуется другая модель расчета с использованием таких макроскопических параметров, как давление p и температура T.

Кинетическая энергия и температура

Эксперименты показывали, что чем горячее вещество, тем с большими скоростями (“энергичнее”) двигаются частицы вещества. Изобретение термометра и введение величины температуры T, позволило ученым не только наблюдать за тепловыми явлениями, связанными с изменением температуры (нагревом и охлаждением), но и проводить измерения, накапливать результаты экспериментов в таблицах, анализируя полученные данные для разных веществ.

Во всех приборах, придуманных в ХVIII веке, измерение температуры сводилось к измерению длины столбика ртути, спирта или воды. Но оказалось, что самыми точными оказались газовые термометры. Дело в том, что жидкостные термометры работали только в ограниченном интервале температур. Наполняющие их вещества замерзали и кипели, и поэтому нельзя было измерять очень высокие и очень низкие температуры. Поэтому газовый термометр до сих пор используется как эталонный для всех температур, достижимых в лабораториях.

Ранее было получено уравнение состояния идеального газа — соотношение между давлением p, объемом V и абсолютной температурой (по шкале Кельвина) T, названное в честь его авторов уравнением Клапейрона-Менделеева:

μ — молярная масса газа, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.

Газовая постоянная R равна:

где: k =1,38*10 -23 Дж/К — постоянная Больцмана, N_a — число Авогадро.

Рис. 2. Постоянная Больцмана.

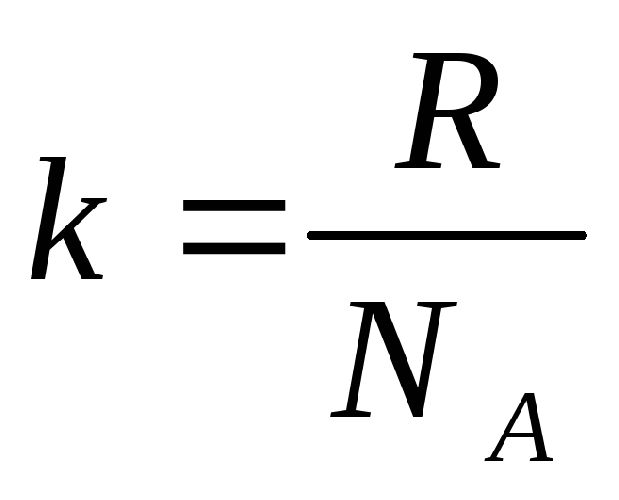
Тогда, из уравнений (4) и (5) получим выражение для давления идеального газа в виде:

В 1860 г. немецкий физик Рудольф Клаузиус получил для давления p одноатомного идеального газа следующую формулу, которую называют основным уравнением молекулярно-кинетической теории:

$ p = <1\over 3>* n * m * v^2_c $ (7),

где: v 2 _c = 2 >_ср — среднее арифметическое квадратов скоростей молекул.

Из двух формул (6) и (7) для величины давления p получаем:

$ p = <1\over 3>* n * m * v^2_c = n * k * T $ (7).

Разделив части уравнения (7) на n, и умножив обе части на 3/2, получим:

Левая часть уравнения (8) представляет собой величину средней кинетической энергии хаотического движения молекул (формула (3)). Таким образом:

Последняя формула (9) демонстрирует, что средняя кинетической энергия хаотического движения молекул идеального газа, а значит и его внутренняя энергия, пропорциональна его температуре T.

Представленные уравнения справедливы для случая одноатомного газа. Дело в том, что у молекул с большим числом атомов кроме чисто поступательного движения появляются дополнительные составляющие энергии: вращательная и колебательная. Поэтому к внутренней энергии добавится энергия вращения молекул и колебаний атомов внутри молекул. Например, молекула кислорода O₂, имеет энергию $ <7\over 2>* k * T $, существенно превышающую энергию одноатомного газа (9).

Что мы узнали?

Итак, мы узнали какие условия должны выполняться для того, чтобы газ был идеальным. Внутренняя энергия идеального газа равна сумме кинетических энергий всех молекул газа. Средняя кинетическая энергия молекул одноатомного идеального газа прямо пропорциональна абсолютной температуре T. На основании уравнений Менделеева-Клапейрона (4) и Клаузиуса (7) получена формула зависимости средней кинетической энергии (9) от температуры T газа.

Источник