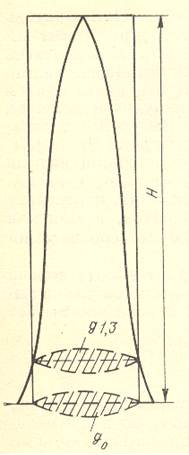
ВИДОВЫЕ ЧИСЛА И КОЭФФИЦИЕНТЫ ФОРМЫ ДРЕВЕСНЫХ СТВОЛОВ
Объем ствола растущего дерева нельзя определить методами, применимыми к срубленным деревьям.
В начале прошлого столетия немецким лесоводом Паульсеном было предложено объем древесногоствола сравнивать с объемом цилиндра. Таким образом, было введено в таксацию понятие видового числа.
Видовым числом называется отношение объема ствола к объему цилиндра, имеющего одинаковую высоту со стволом и площадь основания, равную площади сечения ствола на 1,3 м, высоте груди.
Такой цилиндр называется одномерным со стволом. т. е. видовое число — это отношение объема ствола к объему одномерного ему цилиндра.
Видовое число показывает, какую часть составляет объем ствола от объема цилиндра.
Чем большей величины достигает видовое число, тем ближе ствол приближается к цилиндрической форме и тем он полнодревеснее.
Исходя из формулы можно определить объем ствола
Видовое число, найденное по формулеf =Vств/Vц получило в лесной таксации название старого видового числа.
Старые видовые числа сильно варьируют (изменяются) в зависимости от высоты: чем выше дерево, тем видовое число меньше и наоборот. Старое видовое число не отражает формы древесного ствола.
Позже были выведены нормальные видовые числа. Они более постоянны, не изменяются, отражают форму древесного ствола.
Однако получение таких видовых чисел в практике связано с большими трудностями, так как на стволе необходимо отыскивать 1/20 его высоты и в этом месте измерять диаметр. Из-за указанного недостатка нормальные видовые числа в широкую лесотаксационную практику не вошли, а только для научных работ при составлении соответствующих таблиц.
С целью облегчения нахождения видового числа было предложено брать за основание ствола и цилиндра площадь сечения ствола на высоте 1,3 м от шейки корня. При этом высота ствола и цилиндра уменьшалась на 1,3 м. Такие видовые числа стали называть абсолютными видовыми числами.
Абсолютные видовые числа не зависят от высоты и для стволов определенной формы они являются постоянными величинами.
Видовое число, служащее для определения объема ствола растущего дерева, непосредственно определить трудно, так как формула f =Vств/Vц требует величины объема ствола.
Видовое число связано с коэффициентом формы, причем эта связь позволяет определитьвидовоечисло.
Коэффициентом формы называется отношение диаметра на доле высоты к диаметру на высоте 1,3 м. Чаще всего для определения коэффициентов формы берут диаметр у шейки корня Do и диаметры на высотах, кратных 1/4 высоты ствола (D1/4H, D1/2H, D3/4Н), для краткости записи диаметры обозначают так D0, D1, D2, D3.
Коэффициенты формы соответственно определяются по формулам:
Коэффициенты формы, как и видовые числа, с увеличением высоты и возраста дерева уменьшаются и наоборот. Они характеризуют сбежистость ствола. Чем коэффициенты формы больше по абсолютной величине, тем меньше сбег ствола, а следовательно выше его полнодревесность.
Таким образом, видовое число равно квадрату коэффициента формы g2 2 .
Видовое число также можно определить по формуле
где С — коэффициент, зависящий от породы.
Коэффициент С по существу представляет собой разницу между коэффициентом формы q2и видовым числом. Величина С вычислена для разных пород и составляет: для сосны 0,20; ели и липы 0,21; бука 0,22-0,23; ольхи черной и березы 0,22; осины 0,24.
Приведенные выше формулы позволяют определить видовое число с невысокой точностью, так как они не учитывают связи видового числа с высотой ствола. Связь между видовым числом, коэффициентом формы и высотой ствола носит сложный характер, выражающийся в общем виде уравнением гиперболы.
Австрийский лесовод А. Шиффель нашел, что для ели, сосны это уравнение имеет вид
где Н — высота ствола, м.
По этой же формуле можно определять видовые числа и для других пород. Ошибка при этом не превышает ± 3 %.
Проф. Б. А. Шустов предложил формулу для определения видового числа по высоте и коэффициенту формы:
Проф. М. Е. Ткаченко, исследуя связь между видовым числом, коэффициентом формы и высотой, пришел к выводу, что стволы хвойных и лиственных пород, растущих в насаждениях при любых естественноисторических условиях подчиняются единому закону:
При равной высоте и равных отношениях диаметра на половине высоты дерева к диаметру на высоте 1,3 м ствола деревья всех пород имеют близко равные видовые числа.
На основе этого закона проф. М. Е. Ткаченко составил таблицу видовых чисел.Видовые числа в таблице даются в зависимости от высоты ствола и коэффициента формы g2поэтому она рекомендована автором, как всеобщая.
Малосбежистые и среднесбежистые растут в высокополнотных насаждениях, а сильносбежистые в сильно изреженных древостоях с низкой полнотой.
По древесным породам значение q2 для мало-, средне- и сильносбежистых стволов по древесным породам составляют: у сосны 0,71, 0,65 и 0,59, у ели – 0,80, 0,70, 0,60, у березы – 0,75, 0,60 и 0,57.
В среднем коэффициенты формы стволов q2 равны: сосны – 0,65; ели, пихты и осины – 0,70; дуба – 0,68; березы – 0,66; ольхи черной – 0,68. Для стволов малосбежистых (q2=0,75-0,80), среднесбежистых (q2=0,60-0,70) и сильносбежистых (q2=0,55-0,60).
Источник
ВИДОВОЕ ЧИСЛО



Рассмотренные выше математические способы определения объема ствола требуют не только рубки дерева, но и применения сложных измерений и расчетов. Для определения объема ствола растущего дерева, кроме диаметра на высоте 1,3 м и высоты, используется особый показатель — видовое число, которое обозначается буквой f.
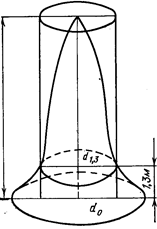
В и д ов ы м ч и с л о м называется отношение объема ствола к объему цилиндра, высота которого равна высоте дерева, а площадь основания равна площади сечения дерева на высоте груди. Такой цилиндр называется равновеликим (рис. 1), т. е.
f=Vcтв/Vцил
Рис. 1. Соотношение размеров ствола и равновеликого цилиндра
Наименование видовое число этот показатель получил от немецкого слова formzahl (форма, вид и число).
Идея использования видового числа была предложена в конце Х1Х века немецким лесоводом Паульсеном и сводится к тому, чтобы объем древесного ствола получить через видовое число, т. е. как произведение объема равновеликого цилиндра на видовое число. Из формулы (1) можно определить объем ствола:
Таким образом, видовое число представляет собой коэффициент, показывающий, какую часть от объема равновеликого цилиндра составляет объем ствола. Зная видовое число, можно легко определить объем растущего дерева по (1), для чего необходимо измерить его высоту и диаметр на высоте груди d1,3.
Так как объем ствола меньше объема цилиндра, то видовое число меньше единицы. Величина fколеблется в пределах 0,352. 0,560, а у деревьев в возрасте их хозяйственного использования (спелости) — в пределах 0,400. 0,500. Это означает, что объем ствола составляет от объема цилиндра 40. 50 %. Чем больше видовое число, тем больше и объем ствола и выше его полнодревесность. У стволов высотой 2,6 м видовое число равно единице, а высотой менее 2,6 м оно больше единицы.
Общеизвестно, что между высотой дерева и его видовым числом существует зависимость, согласно которой с увеличением высоты дерева видовое число уменьшается.
Источник
6.2. Видовые числа
Видовое число есть отношение объема дерева или его части к объему цилиндра, имеющему высоту, равную высоте дерева, и основание, равное площади сечения ствола, взятой на той или иной высоте в нижней части ствола. Видовое число служит показателем его формы.
Длина h отрезка ствола от земли до поперечного сечения, служащего основанием для построения цилиндра, может быть выражена в абсолютных или относительных величинах.
Чаще всего отрезок h берут длиной 1,3 м. Такие видовые числа, представляющие собой отношение объема ствола к объему цилиндра, имеющего со стволом одинаковые высоту и площадь основания, равную площади сечения на высоте груди, получили название старых видовых чисел. Они определяются по следующей формуле:
Соответственно этой формуле объем ствола будет равен
Видовые числа, найденные по формуле (6.4) получили название нормальных видовых чисел.
Применение нормальных видовых чисел затруднено тем, что каждый раз необходимо устанавливать отношение Н/20 и затем уже измерять на этой части высоты диаметр ствола.
Поэтому были предложены постоянные видовые числа для стволов определенной формы, названные абсолютными видовыми числами. При их вычислении площадь сечении ствола на высоте груди принималась за основание, как древесного ствола, так и цилиндра. Высота ствола и цилиндра принималась равной фактической высоте ствола, уменьшенной на 1,3 м. При этом способе вычисления видового числа оно будет равно
Положительной стороной абсолютных видовых чисел является то, что они не зависят от высоты и остаются постоянными для определенной формы ствола. Однако абсолютные видовые числа имеют недостаток, заключающийся в том, что они не характеризуют частей ствола, расположенных ниже высоты груди. Чем короче ствол, тем большая часть его объема приходится на нижнюю часть. Для устранения этого недостатка объем части ствола, расположенной ниже высоты груди, определяют отдельно и складывают с кубатурой ствола, находимой с помощью абсолютных видовых чисел.
В. Гогенадль вывел видовое число, названное им истинным видовым числом. Оно равняется:
где η — отношение диаметров на разной высоте к диаметру на 0,1 общей длины ствола;
V — объем ствола;
W0,1 — объем цилиндра, имеющего диаметр равный толщине ствола на 0,1 его высоты.
В технике таксационных вычислений наибольшее распространение получили старые видовые числа. В результате многочисленных наблюдений собран материал, позволяющий установить средние величины видовых чисел, а также зависимость между ними и диаметрами стволов в разных сечениях.
Объем ствола можно вычислить по простой формуле срединного сечения
где h — высота ствола;
γ — площадь сечения ствола на середине высоты.
Объем цилиндра определяют по формуле Vц = g ∙h, где g — площадь основания цилиндра, при вычислении старого видового числа она равна площади сечения ствола на высоте груди.
Подставив полученные величины в формулу видового числа, получим
где δ— диаметр ствола на середине высоты;
D — диаметр на высоте груди.
Формула (6.7) весьма проста, легко применима на практике и позволяет делать теоретические обобщения в отношении видовых чисел. Однако необходимо иметь в виду, что в ее основе лежит объем ствола, найденный по простои формуле срединного сечения, которая дает по отношению к отдельным стволам значительные ошибки.
Источник
4.1. Видовое число ствола
Особенностью таксации растущих деревьев является недоступность точных замеров на различных протяжениях ствола многих таксационных показателей, в т.ч. диаметров сечений и высоты, а отсюда – и объема ствола.
Поэтому в таксации леса Н.Х. Паульзеном (1800) была высказана идея о сравнении объемов стволов с кубатурой правильных стереометрических тел вращения. В качестве последнего был принят цилиндр. Этот показатель впоследствии получил название «видовое число».
Видовое число есть отношение объема дерева или его части к объему одномерного цилиндра, имеющего с деревом одинаковую высоту, с основанием, равным площади сечения ствола на определенной высоте в нижней его части.
Различают видовые числа:
где g h –площадь сечения ствола на высоте h ; Н – общая высота ствола (дерева);
g i – площадь сечения оцениваемых сучьев на расстоянии l от их основания;
l cуч – общая длина тех или иных сучьев.
Впервые в мировой лесотаксационной практике в 1846 году в России Варгас-де-Бедемар ввел этот показатель под названием «коэффициент полнодревесности ствола» и на основе опытных данных составил таблицы средних видовых чисел для сосны, ели, березы и осины в зависимости от высоты. Установленные им общий характер изменения видовых чисел и их значения почти не отличаются от современных данных.
Видовое число не характеризует образующую ствола, а является лишь коэффициентом полнодревесности цилиндра. Оно используется в таксации леса для перехода от объема цилиндра к кубатуре ствола.
Видовое число правильных тел вращения определяется формулой
где r – показатель формы тела вращения.
В зависимости от h сечения ствола, на которой берется основание одномерного цилиндра, различают следующие категории видовых чисел ствола: старое – 1,3 м; новое – 1/20 Н ; нормальное – 0,1 Н ; абсолютное – 1,3 м (является основанием и ствола, и цилиндра); истинное – 0,1 Н, с определением объема ствола по срединным сечениям 5 равных секций.
В практике лесного хозяйства наиболее распространены старое и нормальное видовые числа (рис. 4.1):
Недостатком старого видового
Рис. 4.1. Соотношение размеров ствола и равновеликого цилиндра
числа является его неравность для стволов одной и той же формы, но различающихся высотами. Так, для квадратного параболоида этот показатель оказывается равным: 0,575 при Н = 10 м; 0,535 при Н = 20 м; 0,522 при Н = 30 м.
В случае же Н = 3,9 м старое видовое число для параболоида ( r = 1) и конуса ( r = 2) составляет
Следовательно, подтверждается ранее высказанное положение, что данное видовое число не может характеризовать форму древесных стволов. Кроме того, выявилось, что этот показатель для стволов древостоя варьирует и меняется в зависимости от ряда факторов.
Нормальное видовое число для правильных тел вращения имеет вид
Его значение не зависит от высоты ствола, а обусловлено лишь формой тела вращения. Проф. В.К. Захаров (1964) считает, что рассматриваемый показатель для стволов данной древесной породы – величина константная: для сосны – 0,521; березы – 0,480…490; дуба –
0,490…0,500; осины и ольхи – 0,540; ясеня – 0,510.
Однако вопрос о нормальных видовых числах еще изучен недостаточно.
Представляет практическое значение изучение связи между старым видовым числом и вторым коэффициентом формы q 2 стволов.
Из анализа формул (2.21) и (4.2) для правильных тел вращения вытекает соотношение
Вейзе (1904), исходя из формул объема ствола по срединному сечению и объема одномерного цилиндра, получил выражение
Однако этот алгоритм справедлив лишь для параболоида ( r = 1). Для отдельных стволов при этом погрешности могут достигать ± 20…25 %.
Кунце (1891), исследуя зависимость между названными показателями, пришел к выводу
где С – постоянная величина для древесной породы (по сосне – 0,20;
ели – 0,21; буку – 0,22…0,23).
Однако позднейшие исследования (Дворецкий, 1956) показали, что значение коэффициента С зависит не от древесной породы, а от высоты и q 2 стволов и составляет в пределах 0,15…0,24.
Гуттенберг (1915) вводит новый поправочный показатель r , названный им фактором среды:
равный для сосны, ели, бука 0,68; пихты – 0,70.
А.Н. Карпов (1955) пришел к выводу, что видовое число ствола определяется выражением
А. Шиффель (1899) на основе анализа материала по ели установил видовое число, по которому ошибки не превышают ± 3 %:
Согласно Фрике (1908), видовое число, выраженное через коэффициенты формы ствола на десятых долях высоты, может быть определено по формуле
По литературным данным, указанная зависимость справедлива лишь для стволов высот более 20 м. В других случаях она показывает значительные погрешности.
По данным проф. Н.В. Третьякова,
Большую работу над выявлением зависимости видового числа от высоты и коэффициента формы q 2 стволов провел проф. М.Е. Ткаченко (1911). Он пришел к выводу, что стволы хвойных и лиственных пород в насаждениях любых естественноисторических условий подчиняются одному и тому же закону формы стволов: при равных высотах и вторых коэффициентах формы стволы всех древесных пород имеют приблизительно равные видовые числа. Основываясь на этом законе, он составил таблицу всеобщих видовых чисел (табл. 4.1). Нормативы эти показаны во многих лесотаксационных справочниках и получили широкое применение.
Таблица 4.1 — Всеобщие видовые числа (по М.Е.Ткаченко)
Коэффициент формы q 2
М.Е. Ткаченко на основании закона формы стволов формулирует важный закон объемов древесных стволов: при одинаковых высоте, коэффициенте формы q 2 и диаметре на высоте 1,3 м стволы всех древесных пород имеют приблизительно равные объемы.
Отмеченные законы являются краеугольным камнем теории и практики таксации леса.
Согласно исследованиям ряда авторов, в изменении старого видового числа древесных стволов в насаждениях проявляются следующие закономерности.
1. С увеличением высоты деревьев видовое число уменьшается. Обратная его зависимость при одинаковой высоте стволов наблюдается и от диаметра на высоте 1,3 м.
2. С ухудшением условий местопроизрастания леса при одинаковых возрастах древостоя видовые числа стволов возрастают. Эта тенденция сохраняется также при одинаковых средних высотах, но разных средних возрастах в этих насаждениях.
3. При прочих равных условиях с увеличением возраста древостоя видовые числа стволов повышаются. Для тонкомерных деревьев это более характерно, чем для толстомерных.
4. С увеличением полноты и густоты древостоя закономерно снижаются процент протяжения кроны и ее развитость, а следовательно, повышаются значения коэффициентов формы и видовых чисел стволов.
По исследованиям А. Шиффеля (1899), в разнородных совокупностях стволов выявлены следующие закономерности в изменении видовых чисел:
а) при одинаковых высотах ствола с увеличением коэффициента
формы q 2 значения видовых чисел возрастают;
б) при одинаковых q 2 с повышением высот стволов значения видовых чисел падают;
в) при одинаковых видовых числах с увеличением высоты стволов
значения коэффициента формы q 2 повышаются.
Отметим, что форма ствола не находится в закономерных, точно определенных связях, взаимоотношениях с формой отдельных тел вращения, образованных по уравнению
При практической таксации возможны погрешности в определении видового числа стволов. В этом случае исходя из формулы объема стволов V = g 1,3 ∙H∙f вытекает положение P V = ± P f , т.е. процент ошибки в объеме равен проценту ошибки в его видовом числе.
Практическое значение видового числа заключается в возможности нахождения объема ствола через кубатуру одномерного цилиндра, в использовании средних значений видовых чисел для составления таблиц объемов стволов, в определении текущего прироста объема стволов
и запасов древостоев.
4.2. Математические методы определения объемов стволов
Применение дендрометров теоретически позволяет измерять диаметры на любых высотах ствола, а следовательно, определять объемы
растущих деревьев теми же способами, что и для срубленных стволов. Однако этот прием очень трудоемок. Поэтому в практике лесоучетных работ применяются приближенные математические формулы определения объемов стволов растущих деревьев, основанные на различных допущениях и упрощениях.
В 1929 г. Денцин вывел упрощенную формулу определения объемов стволов:
при условии f = 0,500 и h = 25 м. Высоту ствола, при которой по алгоритму получается практически правильный объем, он назвал оптимальнoй. Для стволов разных пород онa составляет: для сосны –
28 м, бука – 25 м, дуба – 24 м, ели – 19 + 0,2∙ d 1,3 , пихты – 21 + 0,1∙ d 1,3 . На каждый метр расхождения высот вносится поправка в объем ствола по
Однако исследования проф. М.Л. Дворецкого (1956) показали, что размер оптимальной высоты и значения процентов поправок к полученным результатам зависят от величины коэффициента формы q 2 стволов
Таблица 4.2 — Оптимальные высоты стволов в формуле Денцина
Источник