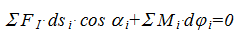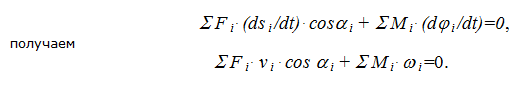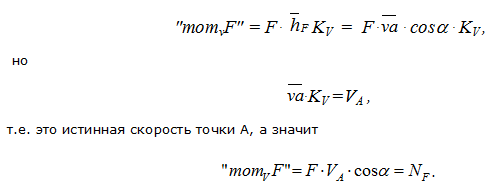Способы определения уравновешивающей силы

Определение уравновешивающей силы способом

Н.Е. Жуковского

Способ основан на принципе возможных перемещений: если система сил находится в равновесии, то сумма элементарных работ на возможных перемещениях точек приложения этих сил равна нулю. Можно поделить все работы на бесконечно малый отрезок времени, за который они совершаются, тогда можно заменить элементарные работы на мгновенные мощности и сформулировать принцип так: если система сил находится в равновесии, то сумма мгновенных мощностей этих сил равна нулю, то есть

.

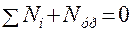
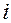
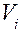
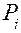
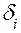
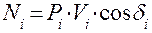
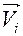
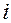
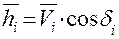
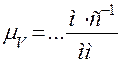
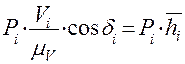
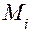
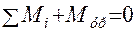
Под знаком суммы в первом слагаемом представлены мгновенные мощности внешних сил, второе слагаемое – мгновенная мощность уравновешивающей силы. Пусть имеется некоторая точка какого-либо звена механизма, движущаяся со скоростью , как показано на рис. 5.6. В этой точке приложена внешняя сила , образующая угол с направлением скорости. Мгновенная мощность этой силы вычисляется по формуле: . Повернём вектор скорости на 90º в любую сторону и переместим вдоль линии её действия так, чтобы она своим концом упиралась в точку . Опустим перпендикуляр из начала повёрнутого вектора скорости на линию действия силы. Длина этого перпендикуляра . Если выражение мощности силы поделить на масштаб скорости , т. е. , то, как видно в правой части выражения, произведение силы на плечо даёт момент этой силы относительно начала повёрнутого на 90º вектора скорости точки приложения силы. Следовательно, мгновенную мощность силы можно представить как её момент относительно повёрнутого вектора скорости точки приложения. Такую операцию можно выполнить с любой внешней силой, тогда вместо равенства нулю мощностей можно записать равенство нулю моментов: . Из этого вытекает следующее положение: если механизм находится в равновесии, то его повернутый на 90º в любую сторону план скоростей с приложенными к нему в соответствующих точках внешними силами как условный жёсткий рычаг также находится в равновесии.

Это положение позволяет определить уравновешивающую силу.

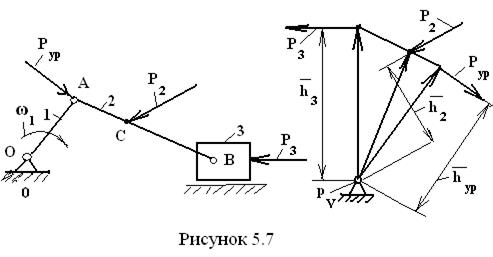
Для решения задачи возьмём кривошипно-ползунный механизм в произвольном положении и приложим к нему две силы, как показано на рис. 5.7. Построим повёрнутый на 90º план скоростей и на концы векторов точек приложения сил перенесём данные силы, сохраняя их заданные направления. К концу вектора скорости точки А кривошипа приложим уравновешивающую силу перпендикулярно кривошипу. Записав уравнение равновесия плана скоростей, как жёсткого рычага, в форме моментов относительно полюса плана, имеем

,

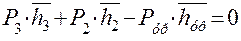
откуда 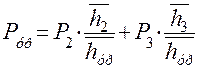. Чёрточки над обозначениями плеч указывают на то, что они берутся в виде отрезков с плана сил. Их перевод в натуральные величины не требуется, так как отношение плеч от масштаба не зависит.

Вопросы для самопроверки

1. Что является основной задачей кинетостатики механизмов?

2. Какие данные должны быть известны для решения задач кинетостатики?

3. В чём заключается принцип Даламбера?

4. В чём заключается принцип освобождаемости?

5. Объясните принцип равенства действия и противодействия в кинематических парах.

6. Какие параметры сил известны и какие неизвестны в кинематических парах?

7. Какие кинематические цепи являются статически определимыми и почему?

8. В каких случаях возникают силы инерции в механизмах?

9. К чему сводится расчёт инерционных воздействий в различных случаях движения звеньев в плоскости? Привести необходимые формулы.

10. В какой последовательности выполняется силовой расчёт механизма?

11. Перечислите методы силового расчёта механизмов.

12. Составьте уравнение равновесия группы Ассура второго класса любого вида в векторной форме.

13. Как определяются тангенциальные составляющие реакций?

14. В чём особенность силового расчёта ведущего кривошипа?

15. Что такое уравновешивающий момент (уравновешивающая сила)? Из какого условия он (она) определяется?

16. В чём отличие определения реакции в кинематической паре кривошипа со стойкой при действии на него уравновешивающего момента или уравновешивающей силы?

Динамика машин

Основными задачами этого раздела являются определение фактической угловой скорости ведущего звена и определение момента инерции маховика, необходимого для поддержания изменения угловой скорости в заданных пределах.

Дата добавления: 2016-01-29 ; просмотров: 1072 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

iSopromat.ru

Определять уравновешивающую силу или момент методом Н.Е. Жуковского можно в случаях, когда требуется найти только неизвестную внешнюю силу без определения реакций в кинематических парах, не прибегая к последовательному силовому расчету всего механизма.

Метод основан на принципе возможных перемещений – если система находится в равновесии, то сумма работ внешних сил и моментов на малых возможных перемещениях равна нулю ( ∑ Ai = 0). Так как с помощью сил инерции (по принципу Даламбера) механизм приведен в состояние равновесия, то в данном случае принцип возможных перемещений применим.

Перейдем к конкретному мгновенному положению механизма, разделив все члены на бесконечно малый промежуток времени (dt), за который происходят указанные малые перемещения:

Таким образом, уравнение работ трансформируется в уравнение мгновенных мощностей и принцип возможных перемещений в применении к механизму можно сформулировать следующим образом – если механизм находится в равновесии, то сумма мгновенных мощностей всех внешних сил и моментов, приложенных к звеньям механизма, равна нулю.

Жуковским Н.Е. был предложен метод составления этого уравнения с использованием плана скоростей (рисунок 19).

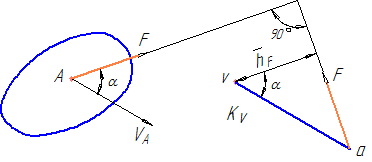
На рисунке 19 изображено некоторое звено, в точке А которого приложена сила F. Скорость V_A этой точки изображается на плане скоростей вектором va в масштабе K_V.

Перенесем силу F в точку «а» плана скоростей, повернув на 90° (в любую сторону). Возьмем формально момент этой повернутой силы относительно полюса плана скоростей:

В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.

Таким образом для составления уравнения Жуковского прикладывают все силы, действующие на звенья механизма (включая силы инерции), в соответствующие точки плана скоростей, предварительно повернув их на 90°. Взяв формально сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получают уравнение развиваемых ими мощностей.

К полученному уравнению добавляют мощности, развиваемые моментами (включая моменты сил инерции).

В уравнение Жуковского мощности должны входить с соответствующими знаками (см. рисунок 16 ). В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.

Примечание: для составления уравнения Жуковского можно на повернутый (на 90°) план скоростей прикладывать силы в своем истинном направлении.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Определение уравновешивающей силы

О п р е д е л е н и е у р а в н о в е ш и в а ю щ е й с и л ы н а о с н о в е п р и н ц и п а в о з м о ж н ы х п е р е м е щ е н и й. Принцип возможных перемещений утверждает: если система сил находится в равновесии, то сумма элементарных работ этих сил на возможных перемещениях их точек приложения равна нулю. Можно поделить все элементарные работы на бесконечно малый отрезок времени, за который они совершаются, тогда их можно заменить мгновенными мощностями и сформулировать принцип так: если система сил находится в равновесии, то сумма мгновенных мощностей этих сил равна нулю, то есть

.

Под знаком суммы в первом слагаемом представлены мгновенные мощности внешних сил, второе слагаемое – мгновенные мощности внешних моментов, третье слагаемое – момент уравновешивающей силы (она тоже относится к числу внешних сил).

Мгновенная мощность силы определяется формулой ,

где 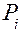– величина i-й силы, H; – скорость точки приложения силы, ; – угол между направлениями силы и скорости.

Мгновенная мощность момента определяется формулой , в которой – момент, действующий на j-е звено механизма, ;
– угловая скорость j-го звена.

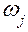
Мгновенная мощность уравновешивающей силы определяется формулой , в которой – величина уравновешивающей силы, Н; – скорость точки приложения уравновешивающей силы, ;
– угол между направлением уравновешивающей силы и скоростью её точки приложения.

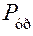
Подставляя формулы для расчёта мощностей в первое уравнение, получаем окончательно

.

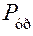
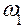
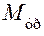
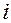
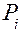
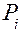
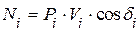
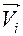
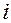
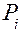
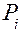
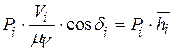
При заданных внешних силах и моментах с помощью этого уравнения нетрудно определить уравновешивающую силу , выбрав произвольно, или учитывая заданные точку приложения силы и её скорость. Если на кривошип действует не уравновешивающая сила, а уравновешивающий момент, то вместо третьего слагаемого в уравнении будет . Так как угловая скорость известна, то уравнение легко решается относительно .

О п р е д е л е н и е у р а в н о в е ш и в а ю щ е й с и л ы с п о м о щ ь ю « ж ё с т к о г о р ы ч а г а » Н . Е. Ж у к о в с к о г о. Пусть имеется некоторая точка какого-либо звена механизма, движущаяся со скоростью , как показано на рис. 4.15. В этой точке приложена внешняя сила , образующая угол с направлением скорости. Мгновенная мощность силы определяется формулой . Повернём вектор скорости , изображённый на рисунке в масштабе , на 90º в любую сторону и переместим вдоль линии его действия так, чтобы он своим концом упирался в точку . Опустим перпендикуляр из начала П повёрнутого вектора скорости на линию действия силы. Длина этого перпендикуляра , т. е. . Если помножить силу на плечо , то получится момент силы относительно точки П, то есть . Таким образом, приходим к равенству , или , и, наконец, , то есть мгновенная мощность силы может быть представлена как её момент относительно начала повёрнутого на 90º вектора скорости точки приложения силы. Причём, величина момента в раз меньше величины мощности данной силы. Такую операцию можно выполнить для любой внешней силы, действующей на механизм. В итоге получится план скоростей механизма, повёрнутый в любую сторону на 90º.

Из этих рассуждений вытекает следующее важное положение: если механизм находится в равновесии, то его повернутый на 90º в любую сторону план скоростей с приложенными к нему в соответствующих точках внешними силами, как условный жёсткий рычаг, также находится в равновесии. То есть условие равновесия плана скоростей как условного жёсткого рычага запишется так: .

В свою очередь, жёстким рычагом Н. Е. Жуковского называется повёрнутый на 90º план скоростей механизма с приложенными к нему внешними силами.

Для решения задачи возьмём кривошипно-ползунный механизм в произвольном положении и приложим к нему две силы, как показано на рис. 4.16 а. К концу вектора скорости точки А кривошипа приложим уравновешивающую силу перпендикулярно кривошипу. Построим повёрнутый на 90º план скоростей и в концы векторов скоростей точек приложения сил перенесём данные силы, сохраняя их направления (рис. 4.16, б). Записав уравнение равновесия плана скоростей, как жёсткого рычага, в форме моментов относительно полюса плана П, имеем

,

откуда . Чёрточки над обозначениями плеч указывают на то, что они берутся в виде отрезков с плана сил. Их перевод в натуральные величины не требуется, так как отношение плеч от масштаба не зависит.

Замечание. Если среди внешних сил имеются моменты, то их целесообразно представить в виде пар сил с плечами, равными длинам соответствующих звеньев.

Вопросы для самопроверки

1. Что является основной задачей кинетостатики механизмов?

2. Какие данные должны быть известны для решения задач кинетостатики?

3. В чём заключается принцип Даламбера?

4. В чём заключается принцип освобождаемости?

5. Объясните принцип равенства действия и противодействия в кинематических парах.

6. Какие параметры сил известны и какие неизвестны в кинематических парах?

7. Какие кинематические цепи являются статически определимыми и почему?

8. В каких случаях возникают силы инерции в механизмах?

9. К чему сводится расчёт инерционных воздействий в различных случаях движения звеньев в плоскости? Приведите необходимые формулы.

10. В какой последовательности выполняется силовой расчёт механизма?

11. Перечислите методы силового расчёта механизмов.

12. Составьте уравнение равновесия группы Ассура второго класса любого вида в векторной форме.

13. Как определяются тангенциальные составляющие реакций?

14. В чём особенность силового расчёта ведущего звена механизма?

15. Что такое уравновешивающий момент (уравновешивающая сила)? Из какого условия он (она) определяется?

16. В чём разница при определении реакции в кинематической паре кривошипа со стойкой при действии на него уравновешивающего момента или уравновешивающей силы?

Источник