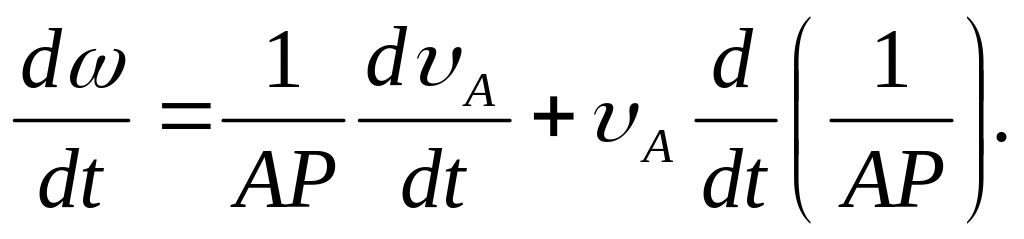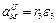- 8. Основные способы вычисления углового ускорения при плоском движении
- 9. Теоерма о конечном перемещении плоской фигуры
- 10. Мгновенный центр вращения. Центроиды
- Вращение твердого тела вокруг неподвижной точки. Общий случай движения тела
- ОСНОВНЫЕ СПОСОБЫ ВЫЧИСЛЕНИЯ УГЛОВОГО УСКОРЕНИЯ ПРИ ПЛОСКОМ ДВИЖЕНИИ
8. Основные способы вычисления углового ускорения при плоском движении
Способы определения углового ускорения:
1. Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение определяем путем дифференцирования их по времени, т.е.
2 
. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным в этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени. Угловую скорость можно найти:
,
где А – точка плоской фигуры; Р – мгновенный центр скоростей.
Дифференцируя по времени, получаем
В тех случаях, когда АР постоянно,
,
; 
,
где 
— касательное ускорение точки А.
Так, например, при качении колеса без скольжения по неподвижной прямой линии, если за точку А взять центр колеса О, то, учитывая, что он движется прямолинейно, получим
.
При качении без скольжения одного колеса по неподвижному другому колесу (рис. 37)
,
где R – радиус неподвижного колеса; r – радиус подвижного колеса.
Дифференцируя по времени, имеем
,
; .
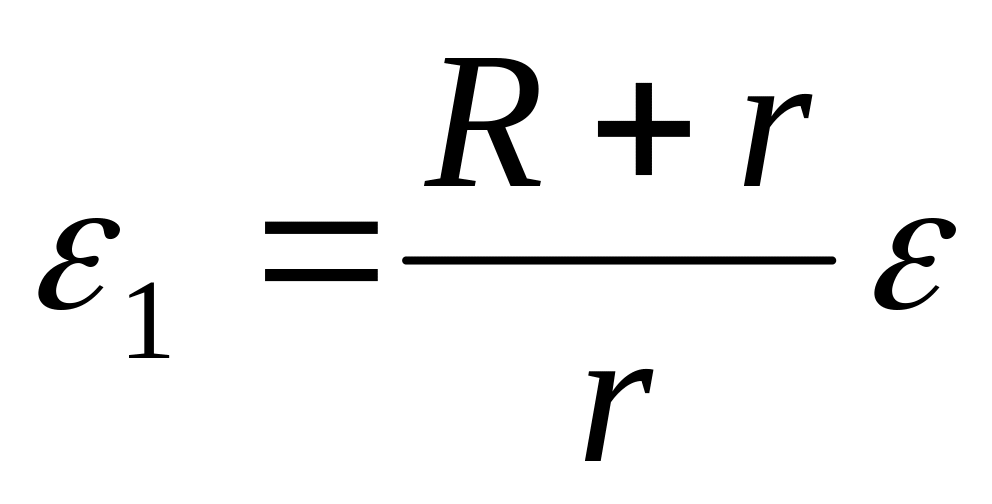
9. Теоерма о конечном перемещении плоской фигуры
Ф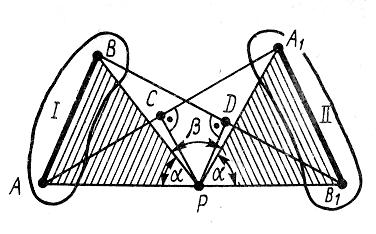 
игуру в ее плоскости из заданного положения I в любое другое положение II (рис.38) можно перевести одним поворотом в этой плоскости вокруг точки P, называемой центром конечного вращения.
10. Мгновенный центр вращения. Центроиды
Для двух бесконечно близких положений плоской фигуры вместо центра конечного вращения получим так называемый мгновенный центр вращения. Любое плоское перемещение фигуры можно приближенно заменить последовательностью вращательных перемещений вокруг своих центров конечного вращения. В пределе плоское перемещение фигуры можно заменить бесконечной последовательностью элементарных мгновенных поворотов вокруг мгновенных центров вращений, расположенных в определенной последовательности.
Отсюда следует, что любое плоское движение фигуры можно заменить последовательностью мгновенных вращений, совершаемых за тот же промежуток времени, что и рассматриваемое плоское движение.
При плоском движении фигуры мгновенный центр вращения перемещается как в неподвижной, так и в подвижной плоскости, скрепленной с движущейся плоской фигурой. Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой, а геометрическое место этих же мгновенных центров вращения на подвижной плоскости, скрепленной с движущейся фигурой, – подвижной центроидой.
При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.
Вращение твердого тела вокруг неподвижной точки. Общий случай движения тела
Ч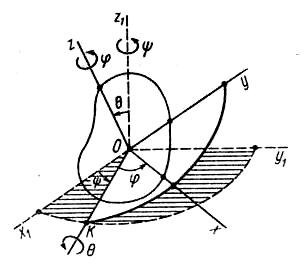 
ерез неподвижную точку О твердого тела проведем неподвижную систему координат O1x1y1 относительно которой будем рассматривать движение тела (рис. 39). Другую систему координат Oxyz скрепим с телом, вращающимся вокруг неподвижной точки О. Для определения положения движущегося тела относительно системы координат O1x1y1 следует задать относительно этой системы координат положение другой, подвижной, системы координат Oxyz, скрепленной с движущимся телом. Для этой цели Эйлер предложил три независимых параметра – углы Эйлера.
Первый из этих углов – угол прецессии – определяет положение линии узлов ОК, которая является линией пересечения координатных плоскостей O1x1y1 и Оху относительно неподвижной координатной оси Ox1. Для изменения этого угла тело должно вращаться вокруг координатной оси Oz1 которую называют осью прецессии.
Вторым углом Эйлера является угол между координатными плоскостями Ox1y1 и Оху. Его измеряют углом между перпендикулярами к этим координатным плоскостям, которыми являются оси Oz1 и Oz.
гол называют углом нутации, а ось ОК, вокруг которой вращается тело при изменении угла , соответственно называют осью нутации или линией узлов.
Для полного определения положения рассматриваемого тела относительно системы координат O1x1y1z1 нужно задать угол между подвижной осью координат Ох и положительным направлением линии узлов ОК – угол собственного вращения . Угол от линии узлов ОК до оси Ох считается положительным, если вокруг оси Oz поворот оси Ох от линии ОК виден происходящим против часовой стрелки.
При изменении угла тело вращается вокруг так называемой оси собственного вращения Oz, перпендикулярной плоскости, в которой лежат прямые ОК и Ох, образующие этот угол.
Углы Эйлера широко применяются в теории гироскопов.
В технике особенно важное значение имеет так называемая регулярная прецессия, когда угловые скорости вращения вокруг оси собственного вращения и вокруг неподвижной оси прецессии постоянны и угол между этими осями (угол нутации) остается тоже постоянным.
Итак, для определения положения тела с одной неподвижной точкой в любой момент времени надо задать углы Эйлера как однозначные функции времени, т. е.
; 
; 
.
Эти уравнения являются уравнениями вращения твердого тела вокруг неподвижной точки.
Источник
ОСНОВНЫЕ СПОСОБЫ ВЫЧИСЛЕНИЯ УГЛОВОГО УСКОРЕНИЯ ПРИ ПЛОСКОМ ДВИЖЕНИИ
При вычислении ускорений точек фигуры при плоском движении необходимо знать угловое ускорение. Рассмотрим некоторые приемы его определения.
1.Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение ε определяем путем дифференцирования их по времени, т.е.
2. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени, считая ее для вывода формулы известной функцией времени. Угловую скорость можно найти по формуле (7)
ω= vA/AP где А-точка плоской фигуры; Р мгновенный центр скоростей .Дифференцируем ω по времени, получаем
Так, например, при качении колеса без скольжения по неподвижной прямой линии (см. рис. 55), если за точку А взять центр колеса О, то, учитывая, что он движется прямолинейно, получим: ε= ao/R, так как в этом случае
где R — радиус колеса.
При качении без скольжения одного колеса по неподвижному другому колесу сначала установим зависимость между угловой скоростью ω1 подвижного колеса и угловой скоростью ю кривошипа ОА (рис. 61). Учитывая, что мгновенный центр скоростей подвижного колеса лежит в точке соприкосновения колес,
где R — радиус неподвижного колеса; r—радиус подвижного колеса. Дифференцируя по времени (21), имеем
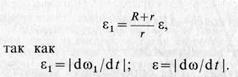
Из сравнения (21) и (22) видно, что связь между угловыми скоростями и угловыми ускорениями колес полностью аналогична. Это справедливо и для углов поворота колес, если нулевые их значения выбрать в один и тот же момент времени.
При внешнем зацеплении дуговые стрелки угловой скорости и углового ускорения подвижного колеса совпадают с дуговыми стрелками соответственно угловой скорости и углового ускорения кривошипа ОА. При внутреннем зацеплении колес дуговые стрелки ε и ω колеса и кривошипа имеют противоположные направления.
3. Иногда угловое ускорение е можно найти путем проецирования на оси координат известного по направлению ускорения, например точки В, если ускорение какой-либо яругой точки А и угловая скорость фигуры ω известны или их можно вычислить предварительно.
Так, если ускорение точки В
то, проецируя обе части (23) на ось Ох, перпендикулярную ускорению ав, получаем соотношение, из которого можно определить угловое ускорение, если другие величины, входящие в это соотношение, известны.
Задание для выполнения по разделу кинематика
II. Определение скорости и ускорения точки по заданным уравнениям
ее движения. Задание К.1.
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в табл. 1.
| Номер варианта | Уравнения движения | t1, c |
| x=x(t), см | y=y(t), ñì | |
| -2t 2 +3 | -5t | 1,5 |
| 4соs 2 (pt/2)+2 | 4sin 2 (pt/2) | |
| -cos(pt 2 /3)+3 | sin(pt 2 /3)-l | |
| 4t+4 | -4/(t+1) | |
| 2sin (pt/2) | -3соз(pt/2)+4 | |
| 3/t 2 +2 | -4/t | 1,5 |
| 3t 2 -t+1 | 5t 2 -5t/2-2 | |
| 7sin(pt 2 /4)+3 | 2-7cos(pt 2 /4) | |
| -3/(t+2) | 3t+6 | |
| -4cos(pt/2) | -2sin(pt/2)-3 | |
| -4/t 2 +1 | -3/t | 1,5 |
| 5sin 2 (pt/4) | 5cos 2 (pt/4)-3 | |
| 5cos(pt 2 /3) | -5sin(pt 2 /3) | |
| -2t-2 | -2/(t+l) | |
| 4соs(pt/2) | -3sin(pt/2) | |
| 3t | 4t 2 +1 | 1,5 |
| 7sin 2 (pt/4)-5 | -7cos 2 (pt/4) | |
| 1+3cos(pt 2 /3) | 3+3cos(pt 2 /3) | |
| 4t 2 -4 | 3t | |
| 2-3t-6t 2 | 3-3t/2-3t 2 | |
| 6sin (t 2 /4)-2 | 6cos(pt 2 /4)+3 | |
| 7t 2 -3 | 5t | 0,75 |
| 4-3t 2 | 4-5t 2 -5t/2 | |
| -4cos(pt/2)-1 | -4sin(pt/2) | |
| -6t | -2t 2 -4 | |
| 8cos 2 (pt/4)+2 | 8sin 2 (pt/4)-7 | |
| -3-9sin(pt 2 /4) | -9cos(pt 2 /4)+5 | |
| -4t 2 +1 | -3t | |
| 5t 2 + 5t/2-3 | 3t 2 +t+3 | |
| 2cos(pt 2 /3)-2 | 2sin(pt 2 /3)+3 |
Пример выполнения задания. Исходные данные:
| x = 4t; у=16t 2 -1; t1 = 0,5 (х и у — в см, t и t1 — в с). | (1) |
| Решение. Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений (1). Получаем у = х 2 — 1, т. е. траекторией точки является парабола, показанная на рис. 6. Вектор скорости точки |  |
| Рис. 6 | |
 | (2) |
 |
Здесь 
— орты осей x и у; 
— проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
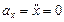 |  | (3) |
 |  |
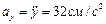По найденным проекциям определяются модуль скорости:
 | (4) |
и модуль ускорения точки:
 | (5) |
Модуль касательного ускорения точки
 | (6) |
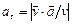 | (6`) |
 | 6« |
выражает проекцию ускорения точки на направление ее скорости. Знак “+” при означает, что движение точки ускоренное, направления 
и 
совпадают; знак “-” — что движение замедленное.
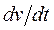
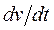
Модуль нормального ускорения точки
 | (7) |
Если радиус кривизны траектории r в рассматриваемой точке неизвестен, то 
можно определить по формуле
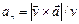 | (8) |
При движении точки в плоскости формула (8) принимает вид
 | (8`) |
Модуль нормального ускорения можно определить и следующим образом :
 | (9) |
После того как найдено нормальное ускорение по формулам (8) или (9), радиус кривизны траектории в рассматриваемой точке определяется из выражения
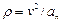 | (10) |
Результаты вычислений по формулам (3)-(6), (8) и (10) для заданного момента времени t1 =0,5 с приведены в табл. 2.
| Координаты, см | Скорость, см/с | Ускорение, см/с 2 | Радиус кривизны, см | |||||||
| x | y | vx | vy | v | ax | ay | a | at | an | r |
| 2,0 | 3,0 | 4,0 | 16,5 | 32,0 | 32,0 | 31,0 | 7,8 | 35,0 |
На рис. 6 показано положение точки М в заданный момент времени. Вектор v строим по составляющим vx и vy причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор а строим по составляющим ax и ay и затем раскладываем на составляющие an и at. Совпадение величин an и at найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 1) добавляется третье уравнение (табл. 3).
Общий порядок выполнения задания в этом случае такой же, как и в приведенном выше примере.
| № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см |
| 3t | 3t | 2t | 1,5t | 4t | 6t | ||||||
| 2t | 2,5t | 3t | 5t | t | 3,5t | ||||||
| 1,5t | 5t | 1,5t | 3,5t | 1,5t | 4t | ||||||
| 4t+4 | 4t+8 | 2t+2 | 6t | 6t | 5t | ||||||
| t | T | 3t | 2t | 2t | 1,5t |
III. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях. Задание К.2.
Движение груза 1 должно описываться уравнением
| х = c2t 2 + c1t + с0, | (1) |
где t — время, с; с0-2 — некоторые постоянные.
В начальный момент времени (t=0) координата груза должна быть х0, а его скорость — v0.
Кроме того, необходимо, чтобы координата груза в момент времени t = t2 была равна х2.
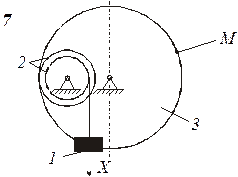
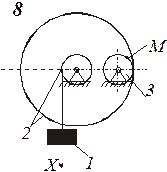
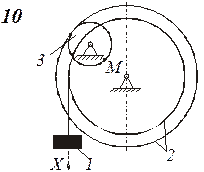
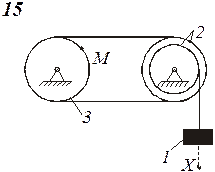
Определить коэффициенты с0, с1 и c2 при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1 скорость и ускорение груза и точки М одного из колес механизма.
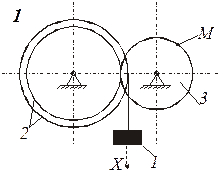
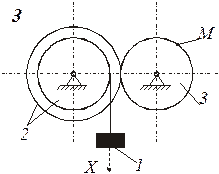
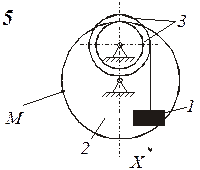
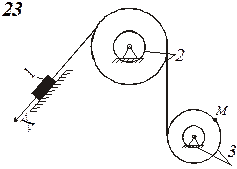
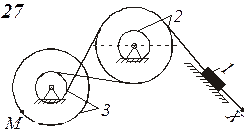
Схемы механизмов показаны на рис. 8-10, а необходимые данные приведены в табл. 4.
| Номер варианта (рис.2-4) | Радиусы, см | Координаты и скорости груза 1 | Расчетные моменты времени, с | |||||
| R2 | r2 | R3 | r3 | x0, см | v0, см/с | x2, см | t2 | t1 |
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| _ | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
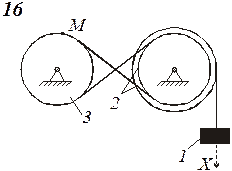Пример выполнения задания. Дано: схема механизма (рис.7); R2=50 см, r2=25 см, R3=65 см, r3=40 см, x0=14 см, v0=5 см/с, x2=168 см, t1=1 с, t2=2 с.
| Найти уравнение движения груза, а также скорости и ускорения груза и точки М в момент времени t=t1. Решение. Уравнение движения груза 1 имеет вид x=c2t 2 +c1t+c0 (1) Коэффициенты с0, с1 и с2 могут быть определены из следующих условий: |  | ||
| Рис. 7 | |||
| при t = 0 | х0 = 14 см |  = 5 см/с | (2) |
| при t2 = 2с | х2 = 168 см | (3) |
Скорость груза 1
v = 
= 2c2t + c1. (4)
Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты
Таким образом, уравнение движения груза 1
х = 36t 2 + 5t + 14. (5)
Скорость груза 1
v = = 72t + 5. (6)
Ускорение груза 1
а = 
= 72 см/с 2 .
Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колес w2 и w2 .В соответствии со схемой механизма
| v=r2w2, R2w2=R3w3 | (7) |
или с учетом (6) после подстановки данных
Угловое ускорение колеса 3
e3= 
=2,215 рад/с 2 .
Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам
; 
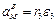
Источник
