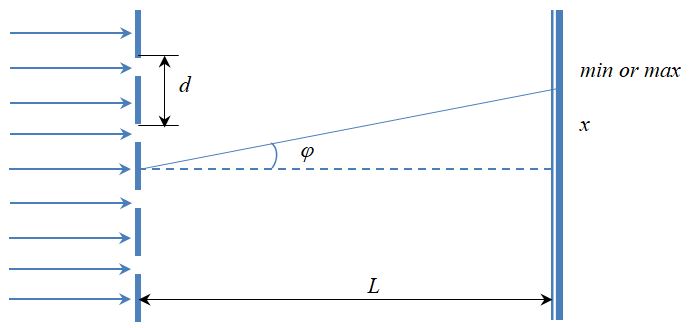
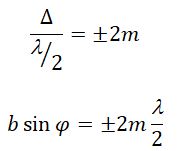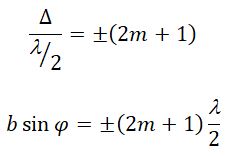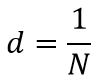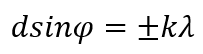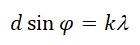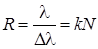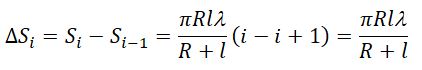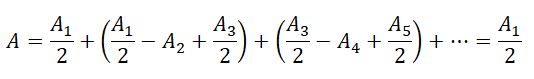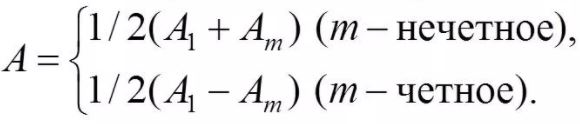Методика определения углового положения дифракционной линии.
Измерения на дифрактограмме позволяют получить профиль дифракционной линии как функцию угла дифракции 2 двумя способами: как непрерывный график или как дискретный график. В качестве параметров характеризующих положение линии, наиболее часто используется положение максимума 2m и центра тяжести дифракционной линии 2с.
Положение 2m в простейшем случае определяют как положение середины хорды, проведённой параллельно линии фона на высоте 1 /3 – 1 /2 от основания линии (соответственно Н /3 или Н /2-метод )
Обычно регистрацию дифрактограммы ведут с применением селективно-поглощательного фильтра на K излучении. При измерении положения -пиков возникают трудности за счёт существования 1-2 дублета. Дублет разрешается тем лучше, чем больше угол , меньше скорость перемещения детектора, меньше входная щель детектора и совершеннее строение изучаемых образцов. В зависимости от степени разрешения дублета, положение линии измеряют в различных точках профиля, и измерения отвечают различным длинам волн: 1, 2 и =(21+2)/3 – средневзвешенной длине волны, соответствующей центру тяжести спектральной линии с с учётом соотношения интенсивностей IK1:IK2 = 2:1.
Сначала измеряют положение единой — линии, а когда появляется возможность разрешить 1 и 2 т.е. когда интенсивность во впадине между ними становится ниже Н /3 или Н /2 то следует измерять уже положение 1. Если при измерениях отсчёт выполняется как по так и по 1, то необходимо перейти к одной системе для проведения расчётов: 
. Точность определения 2m снижается с ростом асимметрии и ширины дифракционной линии.
Метод определения положения центра тяжести дублета 2с свободен от указанных выше сложностей. Координата центра тяжести определяется выражением
, где 20 и 2n — соответственно начальный и конечный углы при которых профиль дифракционной линии переходит в фон; Iл(2) – распределение интенсивности по профилю линии за вычетом фона. Если регистрация линии велась по «точкам» с постоянным шагом (2), то переходя от интегрированию к суммированию с учётом того, что текущее угловое положение детектора
, где Iл(2i)=I(2i)-Iф(2i) – интенсивность линии, за вычетом полной интенсивности фона в точке 2i; n – число шагов перемещения детектора. Предполагается, что интенсивность фона меняется линейно.
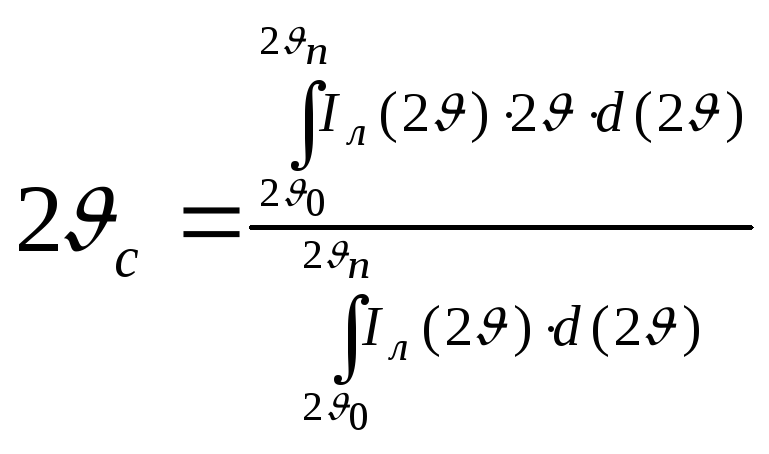
При расчётах с использованием 2с необходимо применять значение длины волны .
Точность измерения как при расчёте по 2m, так и по 2с существенно зависит от относительной погрешности измерения интенсивности уровня фона на дифрактограмме.
Обработка результатов по индицированию.
Съёмка дифрактограммы с образца вольфрама производилась в шаговом режиме. Далее программа ЭВМ автоматически обрабатывала полученные данные, в зависимости от выбранного диапазона расположения дифракционной линии и от степени полинома, аппроксимирующего фон, выводился результат: расположение центра тяжести дублета 2с, максимум интенсивности профиля дублета за вычетом фона, межплоскостное расстояние.
Была произведена обработка результатов для 4-х диапазонов различной ширины, для определения зависимости погрешности от ширины диапазона выборки линии. Полученные данные можно представить в виде таблицы:
Источник
Способы определения угла дифракции
Дифракция — явление отклонения световых волн от прямолинейного распространения при прохождении света мимо края препятствия. При этом лучи могут попадать в область геометрической тени от препятствия.
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн . Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн .
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера . В противном случае говорят о дифракции Френеля . Количественный критерий, позволяющий установить, какой вид дифракции имеет место, определяется величиной безразмерного параметра b 2 /lλ, где b – характерный размер препятствия, l – расстояние между препятствием и экраном, на котором наблюдается дифракционная картина, λ – длина волны.
Свойства дифракции:
1) Дифракция волн – характерная особенность распространения волн независимо от их природы.
2) Волны могут попадать в область геометрической тени (огибать препятствия, проникать через небольшие отверстия в экранах). Например, звук хорошо слышен за углом дома — звуковая волна его огибает. Дифракцией радиоволн вокруг поверхности Земли объясняется прием радиосигналов в диапазоне длинных и средних радиоволн за пределами прямой видимости излучающей антенны.
3) Дифракция волн зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. В пределе при λ→0 законы волновой оптики переходят в законы геометрической оптики. Дифракция обнаруживается в тех случаях, когда размеры огибаемых препятствий соизмеримы с длиной волны.
Объяснить явление дифракции можно исходя из принципа Гюйгенса-Френеля .Этот принцип представляет собой правило, объясняющее, как, исходя из положения волнового фронта в данный момент, найти новое положение волнового фронта в последующий момент времени.
Гюйгенс предложил рассматривать каждую точку среды, которой достигла волна, как источник вторичных сферических волн, распространяющихся по всем направлениям со скоростью, присущей данной среде . Поверхность, огибающая вторичные волны, представляет собой фронт волны в данный момент времени.
Френель дополнил изложенный принцип следующим положением: вторичные сферические волны являются когерентными и колебания в любой точке пространства, которой вторичные волны достигнут в момент времени t, представляют собой результат интерференции этих вторичных волн .
Принцип Гюйгенса — Френеля формулируется следующим образом:
Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.
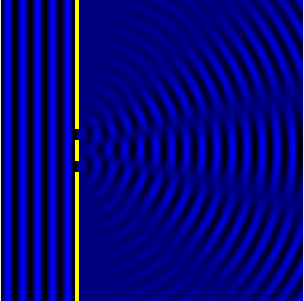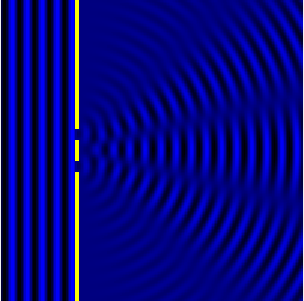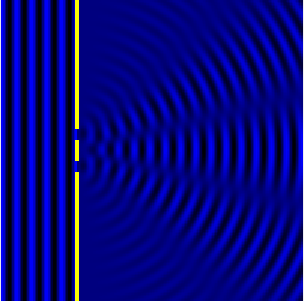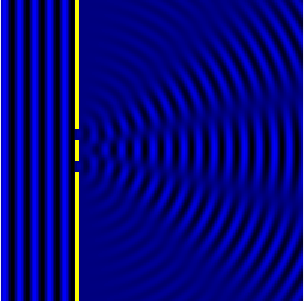
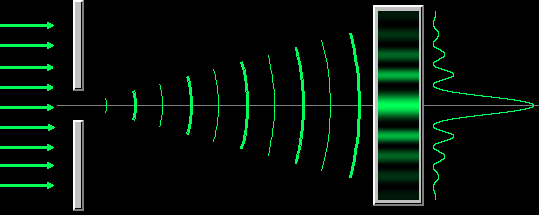
Дифракция Фраунгофера от одной щели
Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.
Разность хода двух волн от краев щели равна Δ = b sin φ .
Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.
Четное число зон Френеля — минимум дифракции
Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:
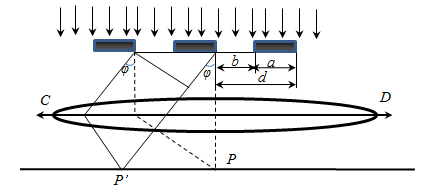
Дифракционная решетка
Совокупность большого числа щелей и промежутков между ними называется дифракционной решеткой.
а — ширина промежутка между щелями;
N — число щелей, приходящихся на единицу длины
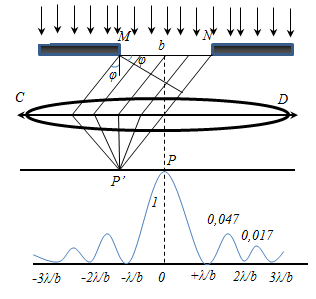
Дифракционная картина на решетке определяется как интерференция волн, приходящих от всех щелей, т. е. дифракция на решетке — многолучевая интерференция. Поскольку щели разделены одинаковым расстоянием, разности хода лучей, поступающих из двух соседних щелей, будут для направления φ идентичны по всей решетке.
В областях, в которых существует минимум при одной щели, минимумы будут и в случае N щелей, т. е. условие первичного минимума дифракционной решетки аналогично условию минимума для одной щели:
— условие главных минимумов.
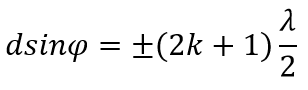
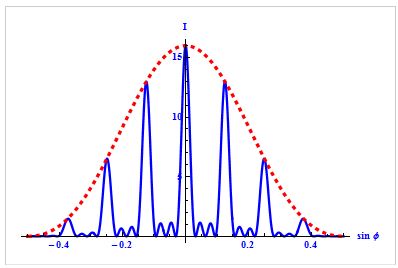
Условие главных максимумов :
Эти максимумы расположены симметрично относительно центра (k = 0) и главного максимума.
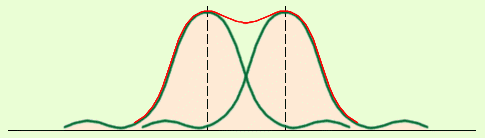
Между основными пиками есть дополнительные очень слабые пики, интенсивность которых значительно меньше, чем у основных пиков (1/22 интенсивности ближайшего главного максимума). Количество дополнительных максимумов равно N — 2, где N — количество штрихов решетки.
Между главными максимумами будут расположены (N-1) дополнительных минимумов.
Разрешающая способность дифракционной решетки
Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Но в высокоточных астрономических приборах реализуется дифракционный предел качества изображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимыми от изображения одной точки.
Спектральной разрешающей способностью R решетки, характеризующей возможность разделения с ее помощью двух близких спектральных линий с длинами волн λ и λ + Δλ, называется отношение длины волны λ к минимально возможному значению Δλ
Пусть решетка имеет период d = 10 –3 мм, ее длина L = 10 см. Тогда, N = 10 5 (это хорошая решетка). В спектре 2-го порядка разрешающая способность решетки оказывается равной R = 2·10 5 . Это означает, что минимально разрешимый интервал длин волн в зеленой области спектра (λ = 550 нм) равен Δλ = λ / R ≈ 2,8·10 –3 нм.
Действие оптических приборов описывается законами геометрической оптики. Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними. Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.
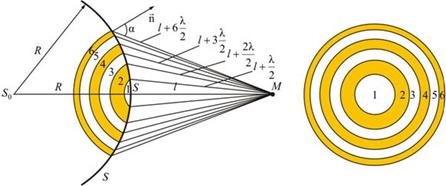
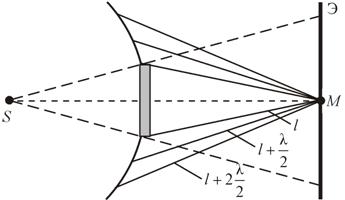
Метод зон Френеля
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии l + λ/2 от точки M. Точки сферы S, находящиеся на расстояниях l + 2λ/2, l + 3λ/2 , и т.д. от точки M , образуют 2, 3 и т.д. зоны Френеля.
Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ = λ/2.
Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: A = A1 + A2 + A3 +. + Ai.
где A – амплитуда результирующего колебания, Ai – амплитуда колебаний, возбуждаемая i-й зоной Френеля.
Величина Ai зависит от площади Si зоны и угла αi между нормалью к поверхности и прямой, направленной в точку M.
Площадь одной зоны
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.
В то же время с увеличением номера зоны возрастает угол αi и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда Ai. Она уменьшается также из-за увеличения расстояния до точки M .
Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.
Приближенно можно считать, что амплитуда колебания A m от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.
.
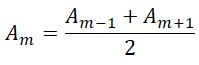
Тогда выражение для амплитуды можно записать в виде
Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда А = A1 /2.
Интенсивность излучения J
Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность J = J1/4 .
Так как радиус центральной зоны мал ( r1 = 0,16 мм), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.
Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна A1. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. J = 4J1 ). Интенсивность света увеличивается, если закрыть все четные зоны.
Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
Дифракция на простых объектах
Дифракция на щели
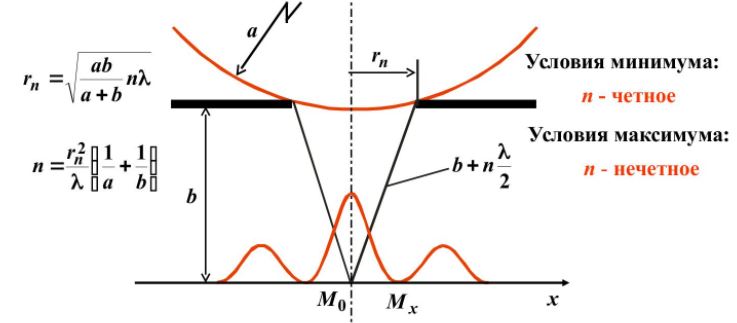
Дифракция от круглого отверстия
Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса . Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.
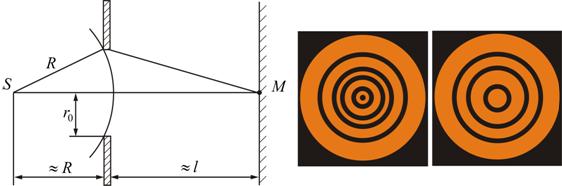
Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. К огда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю.
Дифракция на круглом отверстии при открытом чётном (слева) и не чётном (справа) числе зон.
Естественно, что если r0>>λ, то никакой дифракционной картины не будет.
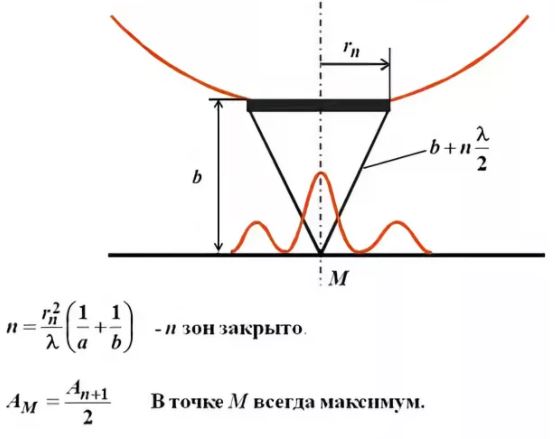
Дифракция от диска
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.
В центре тени светлое пятно
Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).
Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.
Источник
