1.2. Экспериментальные методы определения удельного заряда.
1.2.1. Определение удельного заряда электрона по методу отклонения в электрическом и магнитном полях.
В основе экспериментальных методов определения e/m лежат результаты исследования движения электрона в электрических и магнитных полях.
Необходимо учитывать, что как в случае электрического, так в случае и магнитного поля отклонение в поперечном поле зависит не только от e/m, но и от скорости v. Магнитное отклонение определяется фактором e/mv, а электрическое — фактором 
На рис. 1 представлена схема прибора для определения удельного заряда электрона e/m и скорости v. Нагреваемый током катод K, помещённый в трубку, которая откачана до максимально возможного вакуума, является источником электронов. Эти электроны имеют небольшую тепловую скорость и благодаря разности потенциалов, создаваемой батареей В1, положительный полюс которой присоединён к металлической пластинке (аноду) А, с отверстием в центре, могут существенно ускорится. Электроны, прошедшие через это отверстие, двигаясь прямолинейно, дают на стенке трубки S, покрытой флуоресцирующим веществом, светлое пятнышко F, расположенное против отверстия в аноде А. На пути между анодом А и экраном F электроны проходят между пластинками конденсатора CD, к которым может быть приложено напряжение от батареи В2. Если подключить батарею В2, то пучок электронов отклоняется электрическим полем, возникающем между пластинами, и пятнышко перемещается в положение F’.
Рис. 1. Схема метода определения удельного заряда по отклонению в электрическом и магнитном полях
Создавая между пластинами конденсатора CD также и однородное магнитное поле, перпендикулярное к плоскости чертежа (на рисунке показано точками), можно вызвать отклонение пятнышка в том же или в обратном направлении. Практически удобнее скомпенсировать магнитным полем первоначальное электростатическое отклонение.
В этом случае необходимые измерения сводятся к точному определению напряжённостей обоих полей — электрического и магнитного.
Как сказано выше, начальные скорости электронов, освобождаемых из нагретого катода, малы. Например, если катодом служит вольфрамовая спираль, нагретая до 

Поэтому, зная U, мы уже знаем и скорость электронов. Это освобождает нас от необходимости использовать и электрическое, и магнитное отклонение для нахождения удельного заряда e/m и скорость электрона v. Достаточно воспользоваться либо электрическим (8), либо магнитным полем (5).
1.2.2. Определение удельного заряда электрона по методу двух конденсаторов.
Одним из самых точных современных методов определения удельного заряда электрона e/m является метод двух конденсаторов (схема установки представлена на рис.2). Электроны от нити накала F (см. рис. 2) ускоряются полем между катодом F и анодом А. Пройдя через отверстие в аноде А и диафрагму 


Рис. 2. Схема метода определения удельного заряда при помощи двух конденсаторов
Только те электроны, которые пролетают через конденсатор 


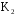
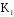
Таким образом, два раза в течение каждого периода в конденсатор 

Нетрудно убедиться, что имеется только два симметричных направления, в которых могут отклониться электроны при прохождении через второй конденсатор 
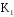
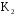






Варьируя скорость электронов v изменением ускоряющего потенциала, можно добиться того, чтобы время 
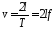

С другой стороны, считая, что электронов кинетическая энергия электронов определяется потенциальной энергией еU, можно записать выражение (8), где U — ускоряющий потенциал, приложенный между катодом F и анодом А.
Учитывая выражения (8) и (10) получим соотношение для удельного заряда

Преимущество метода двух конденсаторов состоит в том, что он является своего рода «нулевым» методом и не требует никаких измерений отклонения, обычно связанных с трудно устранимыми ошибками. Величина удельного заряда, полученная таким способом, после внесения всех поправок равна

1.2.3. Определение удельного заряда электрона по методу фокусировки продольным магнитным полем.
Другой точный метод определения удельного заряда электрона e/m связан с применением продольного магнитного поля.
Рассмотрим, прежде всего, действие магнитного поля на расходящийся пучок электронов, выходящий из одной точки (отверстия диафрагмы). Сила, действующая на электрон со стороны магнитного поля, равна

Если электрон летит под углом α, не равным 0 или 90˚, к направлению магнитных силовых линий, то его скорость можно разложить на две компоненты: продольную 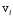



Рассмотрим влияние магнитного поля на каждую из этих компонент отдельно. На электрон, летящий перпендикулярно к полю со скоростью 







Время t, необходимое для того, чтобы электрон описал полную окружность, будет определятся выражением

Следовательно, t не зависит от радиуса ρ. Таким образом, если представить себе несколько электронов, одновременно выходящих из одной точки с различными скоростями 

На продольную компоненту скорости магнитное поле не оказывает влияния. Поэтому за промежуток времени t электроны продвинутся вдоль оси соленоида, создающего поле, на расстояние

Рис. 3. Схема метода определения удельного заряда с помощью продольного магнитного поля. S – отверстие диафрагмы; l— фокусирующее расстояние; О – центр флуоресцирующего экрана; 1-4 – пути движения электронов и соответствующие им проекции на плоскость перпендикулярную оси соленоида.
Если угол α мал, то cosα ≈ 1, и (19) принимает вид

т.е. все электроны, вылетающие из отверстия диафрагмы с одной и той же абсолютной величиной скорости v, за промежуток времени, в течение которого проекции этих электронов на плоскость, перпендикулярную оси соленоида, описывают полную окружность, продвигаются вдоль оси соленоида на одно и тоже расстояние l. Отсюда следует, что расходящийся пучок электронов одинаковой энергии под действием продольного магнитного поля сфокусируется на расстоянии l.
Это фокусирующее действие соленоида и лежит в основе метода продольного магнитного поля. Электроны, выходящие из отверстия диафрагмы S (рис. 3) и развернутые предварительно в расходящийся пучок переменным электрическим полем E, попадают внутрь соленоида. Подбирая соответствующую величину напряжённости магнитного поля Н, можно добиться того, чтобы пучок электронов фокусировался как раз у противоположного к диафрагме конца соленоида, где помещён флуоресцирующий экран. Зная необходимое для этого значение поля, можно вычислить удельный заряд электрона e/m. Действительно, из (20) находим

Подставляя это выражение для скорости в уравнение (12), легко получим для удельного заряда электрона

Результат измерений, выполненных этим методом, таков:

Наиболее точное значение удельного заряда электрона, полученное в результате критической оценки измерений, выполненных различными методами, есть
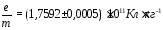
Сравним теперь массу электрона с массой атома водорода. Для этого нужно, прежде всего, найти величину 
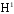


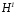

Комбинируя (24) и (25) , находим

Итак, масса электрона в 1837,5 раза меньше массы атома водорода.
1.2.4. Определение удельного заряда электрона методом магнетрона.
Магнетрон — это двухэлектродная электронная лампа (диод), в которой управление током осуществляется внешним магнитным полем. Это поле создаётся соленоидом, внутри которого расположена лампа. Накаливаемый катод и холодный анод этой лампы имеют форму коаксиальных (соосных) цилиндров (см. рис. 4).
Линии электрического поля E внутри магнетрона направлены радиально от анода к катоду, а постоянное магнитное поле B направлено вдоль оси катода. Таким образом, магнитное и электрическое поля взаимно перпендикулярны. Напряжённость поля Е максимальна у катода. В случае если катод имеет форму тонкой нити, величина Е, пропорциональная 1/r, быстро уменьшается с ростом расстояния r от катода. Поэтому изменение скорости электронов до значения, равного v, происходит, в основном, вблизи катода, а при дальнейшем движении можно считать скорость практически постоянной.
Рис.4.Схема магнетрона: А — холодный анод; К — накаливаемый катод.
Электрон, ускоренный разностью потенциалов U, приобрёл кинетическую энергию, определяемую соотношением (8), из которого можно определить скорость
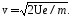
В отсутствие магнитного поля электроны, эмитированные катодом, движутся под действием электрического поля E прямолинейно в радиальных направлениях. При этом в анодной цепи протекает ток, величина которого зависит от анодного напряжения и тока накала катода. При помещении лампы в магнитное поле В на движущиеся электроны действует сила Лоренца. Она перпендикулярна линиям B, т.е. лежит в одной плоскости с вектором скорости электрона v, нормальна ему и сообщает частице центростремительное ускорение. Согласно второму закону Ньютона

Таким образом, электрон в магнетроне будет двигаться по окружности, радиус которой

будет уменьшаться с ростом индукции магнитного поля.
Рис. 5(а). Траектория движения электрона при увеличении
магнитной индукции (В)
Рис. 5(б). Зависимость анодного тока от индукции магнитного поля
На рис. 5(а) показано, как изменяются траектории движения электрона в цилиндрическом магнетроне по мере увеличения магнитной индукции.
Существует критическое значение магнитной индукции 
где r — радиус анода.
Согласно соотношениям (28) и (29) значение 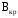


Если величина 
Если 
При 
Определив критическое значение индукции магнитного поля 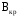

Индукцию В для поля короткого соленоида (см. рис.6) вычисляют по формуле:
Рис. 6. Сечение короткого соленоида для расчета величины индукции В
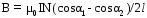
где 
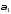


где d — диаметр соленоида.
Подставляя значения косинусов в формулу (32), получаем критическую величину магнитной индукции:

где 

С учётом выражения (34) расчётная формула (31) для определения удельного заряда электрона принимает следующий вид:

Источник











