Способы определения точек пересечения прямой плоскостью

Определение точки пересечения прямой с плоскостью

Для определения точки пересечения прямой с плоскостью пользуемся следующим алгоритмом: прямую заключаем во вспомогательную плоскость, находим линию пересечения этих двух плоскостей (заданной и вспомогательной), и линия пересечения плоскостей в пересечении с заданной прямой даст искомую точку. Последним этапом в построении является определение видимости прямой при помощи конкурирующих точек.

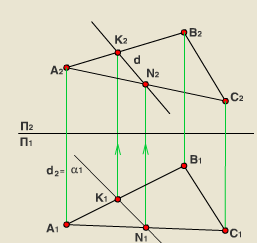
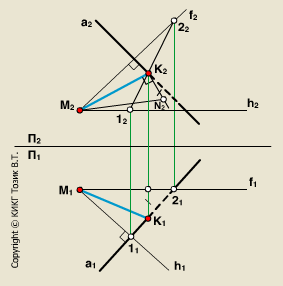
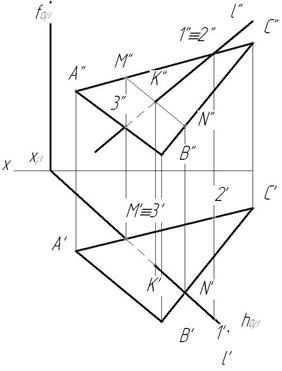
Пример1. Плоскость задана следами (рис.70)

Рис.70

1. Для построения точки пересечения прямой lс плоскостью необходимо через прямую провести вспомогательную плоскость частного положения, например, фронтально-проецирующую β π₂, l» f_оβ, f_оβ – собирающий след, h_оβ х (рис.71).

Рис.71

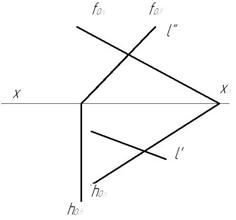
2. Строим линию пересечения MN заданной и вспомогательной плоскости М’=h_оα∩ h_оβ, N»= f_оβ∩ f_оα (рис.72).

Рис.72

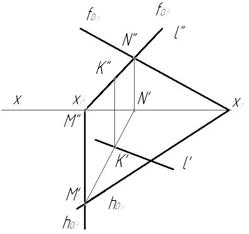
3. Определяем точку пересечения К заданной прямой l с линией пересечения MN. К’=М’N’∩l ‘, К» – в пересечении линии проекционной связи, проведенной из К’ и l ».

4. Видимость прямой l в случае задания плоскости следами не определяем.

Пример 2. Пересечение прямой с проецирующей плоскостью (рис.73).

При построении точки пересечения прямой с проецирующей плоскостью задача упрощается, т.к. одна из проекций искомой точки будет лежать на собирающем следе. На рис.73 дана горизонтально-проецирующая плоскость. Искомая точка К будет одновременно принадлежать плоскости α и прямой а.

Рис.73

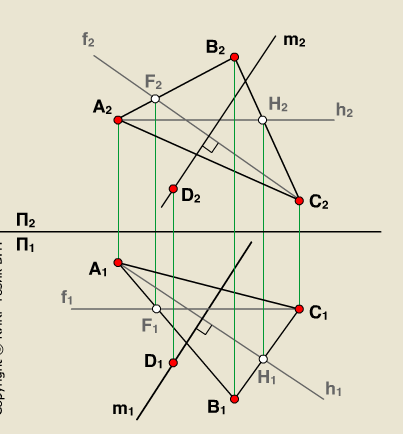
Пример 3. Плоскость задана плоской фигурой (рис.74).

Рис.74

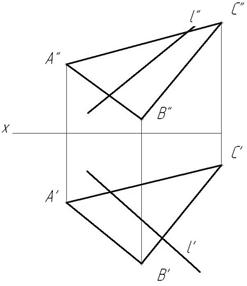
Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую β π₁.l‘ h_оβ, h_оβ – собирающий след, f_оβ х (рис.75).

Рис.75

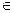
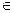
2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М’=А’С’∩ hоβ М» А»С» и N’=В’С’∩ hоβ N» »ѻ (рис. 76).

3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К»= М»N»∩l». К’ находится в пересечении линии проекционной связи, проведенной из К» и М’N’.

4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.

Определяем видимость относительно плоскости π₂ .Отметим фронтальную проекцию 1» совпадающую с 2». Горизонтальную проекцию 2′ отметим на А’С’, а 1′ на l’. Горизонтальная проекция 1′ лежит перед 2′, следовательно, фронтальная проекция 2» не видима относительно π₂. Точка 1 лежит на прямой l, она видима на π₂, следовательно, фронтальная проекция l» от 1″2» до К» видима, в точке К» видимость меняется на противоположную.

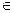
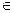
Определим видимость прямой l относительно плоскости π₁. Отметим горизонтальную проекцию 3′, совпадающую с горизонтальной проекцией М’. М» А»С» уже отмечена, 3» l’‘. Фронтальная проекция М» лежит выше фронтальной проекции 3», следовательно, точка М видима относительно π₁. Точка 3 лежит на l, следовательно, от М’≡3′ до К’, горизонтальная проекция l’ невидима. В горизонтальной проекции К’ видимость меняется на противоположную. За границами ΔАВС прямая l везде видима.

Рис.76

Источник

1.Способы определения точек пересечения прямой с плоскостью, с гранной поверхностью.

Если прямая и плоскость не параллельны, то они пересекаются в точке, которая принадлежит как прямой, так и плоскости.

Определение точки пересечения прямой lс плоскостьюABCв общем случае выполняется в такой последовательности:

– через прямую проводят вспомогательную проецирующую плоскость, например, απ₂; ее следα»совпадает с фронтальной проекцией прямой;

– находят линию MNпересечения плоскостейαиABC;

– фиксируют точку Oпересечения прямойlи прямойMN(в данном варианте сначала определяется проекцияO’).

Видимость прямой lпо отношению к плоскостиABCопределена с помощью пар конкурирующих точекFиG,MиP.

2. Построение линии пересечения плоскости частного и общего положения, двух плоскостей общего положения.

Для построения линии пересечения двух плоскостей a и b необходимо найти две точки, N и M каждая из которых принадлежит обеим плоскостям. Для нахождения точек N и M можно воспользоваться следующим алгоритмом:

Общ+час: Спроецируем плоскости a и ABC на П1. Плоскость общего положения АВС проецируется на плоскость П1 в виде треугольника А1В1С1, а плоскость частного положения a — в виде прямой a1. На плоскости П1 прямая a1 и АВС пересекаются в точках K1 (K1 принадлежит А1В1) и N1 (N1 принадлежит А1C1). Если через точки K1 и N1 провести проецирующие прямые до пересечения с плоскостью АВС, то получатся две точки K (K принадлежит АВ) и N (N принадлежит АC). Соединив точки K и N, мы получим прямую KN. Прямая KN — линия пересечения плоскости a с плоскостью АВС.

1)Взять две дополнительные плоскости частного положения 1ЧП и 2ЧП;

2)Определить линии пересечения плоскостей частного положения 1ЧП и 2ЧП с плоскостями

общего положения a и b с помощью метода, приведенного в предыдущем пункте;

3)Определить точки N и M пересечения полученных линий.

3.Перпендикулярные прямые. Привести пример определения расстояния от точки до прямой общего положения.

Пересекающиеся и скрещивающиеся прямые в пространстве могут располагаться в частности под прямым углом друг к другу. Если обе прямые – общего положения, то факт их перпендикулярности на чертеже не отражается: проекцией прямого угла будет тупой (острый) угол.

И только в случае, если одна из прямых параллельна плоскости проекций, прямой угол проецируется в натуральную величину на ту плоскость, которой прямая параллельна. Это предложение (теорема) является основополагающим для изображения на чертеже взаимно перпендикулярных прямых: тогда и только тогда прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций, а следовательно, является или фронталью, или горизонталью.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую. Пусть необходимо определить расстояние от точки М до прямой а общего положения.

Через заданную точку M проводится плоскость s перпендикулярная заданной прямой а. Плоскость задается двумя пересекающимися прямыми, фронталью (f) и горизонталью (h): s = h f.

Находится точка пересечения (K) исходной прямой а с плоскостью s.

Определяется расстояние от точки М до точки K способом прямоугольного треугольника. Длина гипотенузы прямоугольного треугольника M2K2N2 равна расстоянию от точки M до прямой а: |MK| = M2N2.

4.Перпендикулярные прямая и плоскость. Привести примеры определения расстояния от точки до плоскости частного положения, от точки до плоскости общего положения. Привести пример построения перпендикуляра заданной длины к плоскости общего положения в точке, принадлежащей плоскости.

Прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым этой плоскости.

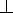
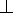
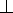
Для того, чтобы прямая mбыла перпендикулярна плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямойm₁былагоризонтальной проекции горизонтали (m₁h₁), а фронтальная проекция прямойm₂– фронтальной проекции фронтали (m₂f₂).

Расстояние от точки до плоскости является длина перпендикуляр опущенного из данной точки к данной плоскости.

Длину перпендикуляра можно определить с помощью прямоугольного треугольника.

Для построения перпендикуляра заданной длины для начала необходимо построить перпендикуляр произвольной длины, а затем увеличивая гипотенузу можно получить перпендикуляр заданной длины.

5.Перпендикулярные плоскости. Привести пример построения плоскости, перпендикулярной двум заданным плоскостям. Привести пример построения плоскости, параллельной заданной прямой и перпендикулярной заданной плоскости.

Известно, что плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Поэтому, построение плоскости, перпендикулярной данной, предполагает построение перпендикуляра к ней из любой точки, заведомо принадлежащей искомой плоскости.

Известно, что прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости. Например, прямая m параллельна прямой l, лежащей в плоскости

Источник

Построение точки пересечения прямой и плоскости

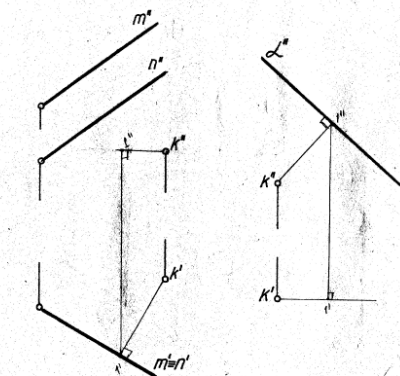
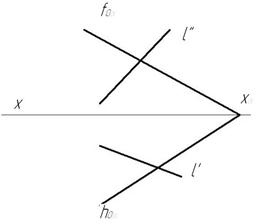
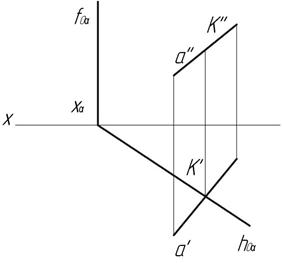
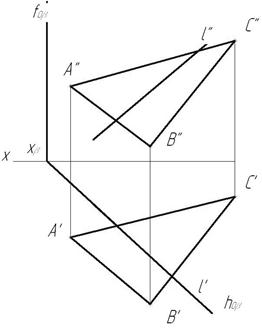
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h_0α, f_0α.

1. Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h_0γ, f_0γ.
2. Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h_0α ∩ h_0γ, A» = f_0α ∩ f_0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
3. Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.

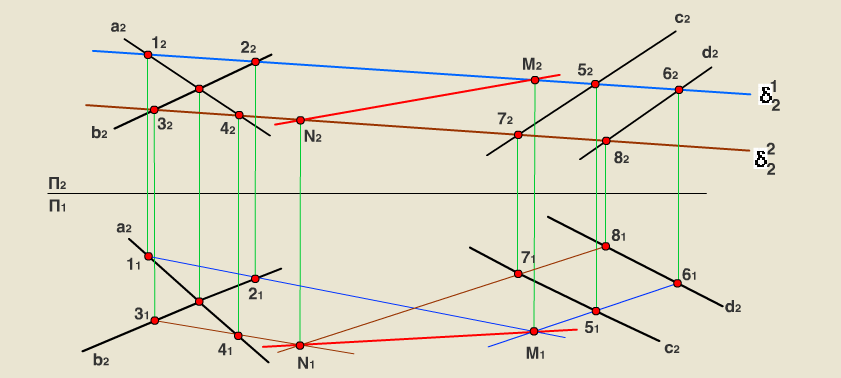
Видимость прямой a относительно плоскости α. Метод конкурирующих точек

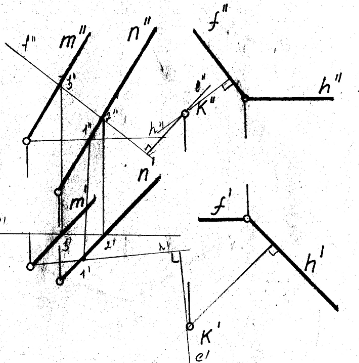
1. Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П₂ на разное расстояние.
2. Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П₂ на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
3. Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П₁ на разное расстояние.
4. Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П₁ на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.

Источник