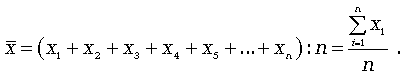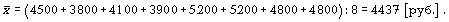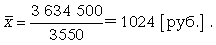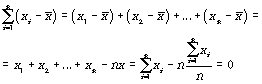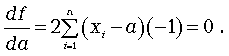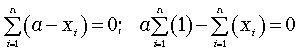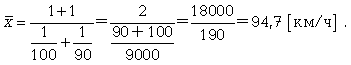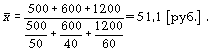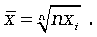Способы определения средних величин

Тема 5: Средние величины

5.1 Сущность средних величин

5.2 Виды средних величин и способы их расчета

5.3 Математические свойства средней арифметической. Упрощеный метод расчета средней арифметической.

5.4 Структурные средние

5.5 Показатели вариации.

5.1.Сущность средних величин.

Средняя величина – это обобщающий количественный показатель, характеризующий типичный уровень совокупности по определенному признаку. Средняя величина является наиболее распространеной формой статистических показателей, используемых в экономических исследованиях.

Основные черты средней величины, как типичной характеристики явления:

1.Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.

2. Средняя величина представляет значения оприделенного признака совокупности одним числом, несмотря на количественные различия у отдельных единиц совокупности.

3. Средняя величина абстрагируется от индивидуальных значений признака отдельных единиц совокупности и отражает то общее, что содержится в каждом отдельном единичном.

4. Средние величины тесно связаны с законом больших чисел.

5.2. Виды средних величин и способы их расчета

Виды средних величин:

1) Самый распространенный вид средней величины — это средняя арифметическая.

В общем случае ее расчет сводится к суммированию всех значений варьирующего признака и делению полученной суммы на количество единиц совокупности.

Средняя арифметическая может быть:

а) средняя арифметическая простая

x_i — варианты осередняемого признака

n— число единиц совокупности

Средняя арифметическая простая применяется в тех случаях, когда значение каждого варианта встречается по одному разу

б) В тех случаях, когда значение вариантов встречаются несколько раз, для расчет применяют среднюю арифметическую взвешанную.

f_i — частота этих вариантов.

В случае определения средней величины в интервальном ряду распределения сначала переходят от интервального к дискретному ряду, т.е. находят середину интервалов в каждой группе, как полусумму нижней и верхней границ в каждой группе.

2) Средняя гармоническая применяется в тех случаях, когда известны варианты осередняемого признака (x_i) и показатели, представляющие произведение вариантов на частоты или веса средней арифметич.

Это произведение x*f=F и служит в качестве весов или частот средней гармонической.

Средняя гармоническая может быть простой и взвешанной.

а) средняя гармоническая простая

x_i — варианты осередняемого признака

n— число вариантов осередняемого признака

Средняя гармоническая простая применятся в тех случаях, когда веса всех вариантов равны. В тех случаях, когда веса не равны, применяется средняя гармоническая взвешанная.

б) средняя гармоническая взвешанная

Средняя гармоническая — это средняя из обратных величин, поэтому ее применяют для расчета средней трудоемксти, которая является обратной величиной производительности труда (выработки).

На практике чаще всего применяются средняя арифметическая и средняя гармоническая. Чтобы правильно выбрать формулу средней, необходимо руководствоваться следующими правилами:

1. Средняя гармоническая применяется для расчета в тех случаях, когда показатеь, величина которого не известна находится в знаменателе исходного отношения (это экономическое содержание расчитываемое показателем)

ЗП=ФондЗП/ЧР

2. Если в искомом отношении не известен числитель, то для расчета применяют среднюю арифметическую взвешенную.

3) Средняя геометрическая применяется в тех случаях, когда определяемый показатель является не суммой значения признака, а их произведением, т.е. во всех случаях, где варианты связаны между собой не знаком «+», а знаком «*» расчитывают не среднюю арифметическую, а среднюю геометрическую. Средняя гармоническая бывает простая и взвешанная.

а) средняя геометрическая простая

x_i — варианты осередняемого признака; n— число вариантов осередняемого признака

Применяется, когда варианты встречаются по одному разу.

В тех случаях, когда разное число вариантов, применяется

б) средняя геометрическая взвешенная

Ср. геом. простая применяется в экономических исследованиях для расчета среднего коэффициента роста. Ср. геом. взвешенная применяется для расчета средних величин, когда значения признака заключены в групповые интервалы. В этих случаях в качестве значения признака необходимо брать не значение их середины интервала, а log их полусуммы.

4) Средняя квадратичная применяется при осереднении величин, выраженных в виде квадратичной функции.

Применяется, когда варианты встречаются по одному разу. Применяется на практике редко. Ее используют в основном для расчета средних диаметров труб, средних сторон квадрата.

Между перечисленными средними величинами, рассчитанными по одной и той же совокупности единиц и по одному и тому же признаку существует следующая взаимосвязь:

5) Средняя хронологическая применяется для расчета средних величин в моментных рядах, когда значения признака представлены в хронологическом порядке через равные промежутки времени.

5.3 Математические свойства средней арифметической. Упрощеный метод расчета средней арифметической.

Определение средней арифметической в ряде случаев связано (при очень большой численности совокупности) с большими затратами времени и средств. Однако процедуру расчета средней можно упростить, если использовать некоторые ее свойства. Приведем без доказательства основные свойства средней арифметической:

1) средняя арифметическая от постоянной величины равна ей самой

2) произведение средней на сумму частот равно сумме произведения вариантов на их частоты

3) изменение каждого варианта на одно и тоже число и на одну и ту же величину изменяет среднюю на ту же величину

4) изменение каждого из весов (частот) в одно и тоже число раз не меняет величины средней

5) изменение каждого варианта в одно и тоже число раз изменяет среднюю во столько же раз

6) сумма отклонений каждого варианта от их средней равна нулю

7) средняя суммы равна сумме средних величин

Рассмотренные свойства средней арифметической используются для упрощения расчетов связанных с вычислением средней величины.

Метод упрощения вычисления средней арифметической называется методом условных моментов или методом отчета от условного нуля.

Согласно этому методу средняя рассчитывается по следующей формуле.

x₀ – значение условного нуля

h – ширина интервала

m₁ – условный момент первого порядка

Расчет средней арифметической способом условных моментов применяется для расчета средних в интервальных вариационных рядах.

5.4 Структурные средние.

В статистическом анализе кроме рассмотренных средних используют величины конкретных вариантов, которые занимают в упорядоченном ряду значений признака определенное положение. Это мода, медиана, квартири, децили, процентили. Эти средние называют структурными средними.

1) Медиана — это вариант расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части, таким образом, что у одной половины единиц совокупности значения варьирующего признака меньше медианы, а у другой — больше.

Рассмотрим расчет медианы в вариационных рядах (дискретный и интервальный).

а) В дискретном вариационном ряду с четном числом вариантов медиана рассчитывается как среднее значение двух вариантов, имеющие порядковые номера n/2 и n/2+1.

В этих рядах с нечетным числом членов медиана рассчитывается по формуле n+1/2

б) В интервальных рядах медиана начинается с определения интервала, в котором находится медиана. Этот интервал называется медианный интервал. Этот интервал характерен тем, что его кумулятивная частота (сумма накопленных частот) равна или превышает полусумму всех частот ряда. После того, как нашли медианный интервал, значение медианы рассчитывается по следующей формуле:

X_ME – нижняя граница медианного интервала

h – ширина медианного интервала

S_ME_-1 – кумулятивная частота, накопленная до медианного интервала.

2) Мода – это вариант, который чаще всего встречается в данной совокупности. Рассмотрим расчет моды в вариационных рядах:

а) В дискретном вариационом ряду модой является вариант обладающий наибольшей частотой.

б) в интервальном вариационном ряду расчет моды осуществляется в следующем порядке:

1. определяем модальный интервал, т.е. интервал обладающей наибольшей частотой;

2. производим расчет моды по формуле

X_M₀ – нижняя граница модального интервала

h – ширина модального интервала

f_M₀ – частота модального интервала

f_M_0-1 – частота предмодального интервала

f_M₀₊₁ – частота послемодального интервала

3) Наряду с медианой для полной характеристики изучаемой совокупности применяют:

а) квартири — делят ряд на 4-е равные части, из будет 3.

б) децили — делят ряд на 10 равных частей, их будет 9.

в) процентили — делят ряд на 100 равных частей, их будет 99

5.5 Показатели вариации.

Вариация – это такие количественные изменения величины исследуемого признака в пределах статистической совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.

Например: размер зарплаты рабочих зависит от ряда факторов (специальность, разряд, стаж работы). Чем больше различия между значениями указанных факторов, тем больше вариаций в уровне заработной платы рабочих. Для характеристики вариации используют абсолютные и относительные показатели вариации.

1) Абсолютные (размах вариации) показатели – R – рассчитывается, как разница (..).

Чем меньше значение этого показателя, тем совокупность однороднее. Недостаток этого показателя в том, что он не учитывает изменения значений признака внутри предельных значений вариантов.

Вместе с тем для характеристики вариации признака необходимо знать не только размах предельных значений отклонений но и уметь обобщить отклонения всех значений от какой-либо типичной для изучаемой совокупности величины(средней). Такую характеристику вариаций дает среднее линейное отклонение.

Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической.

— это невзвешенное среднее линейное уравнение.

Применяется для вариационного ряда с равными частотами.

— это взвешенное.

Дисперсия — это средний квадрат отклонений вариантов от их средней арифметической.

— это простая дисперсия, которая применяется для в вариационных рядах с равными частотами.

В вариационных рядах с неравными частотами рассчитывают дисперсию взвешенную.

Для интервальных вариационных рядов с равными интервалами дисперсия рассчитывается способом условных моментов.

h – ширина интервала

m₁ – условный момент 1-го порядка

m₂ – условный момент второго порядка

2) Относительные показатели.

В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, сравнение вариации возраста рабочих и их квалификации, стажа работы и размера из з/п. Для таких сопоставлений абсолютные показатели вариации нельзя и использовать, тюк нельзя сравнивать вариацию стажа работы, выраженного в годах с вариацией з/п, выраженной в леях. Для таких сравнений используют относительный показатель вариации, который наз-ся коэффициентом вариации.

Коэффициент вариации применяется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Если к.в. меньше 30 %, то совокупность является однородной.

Источник

Виды средних величин и методы их расчета

На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.

Используются две категории средних величин:

степенные средние;
структурные средние.

Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую.

Вторая категория (структурные средние) — это мода и медиана. Эти виды средних будут рассмотрены в теме «Ряды распределения».

Введем следующие условные обозначения:

— величины, для которых исчисляется средняя;

— средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;

— частота (повторяемость индивидуальных значений признака).

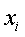
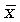
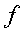
Различные средние выводятся из общей формулы степенной средней:

(5.1)

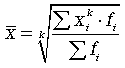
при k = 1 — средняя арифметическая; k = -1 — средняя гармоническая; k = 0 — средняя геометрическая; k = -2 — средняя квадратическая.

Средние величины бывают простые и взвешенные.

Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом или весом средней.

Средняя арифметическая — самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая — это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

Формула средней арифметической (простой) имеет вид:

(5.2)

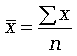
где n — численность совокупности.

Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая:

Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек:

При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным.

В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид:

(5.3)

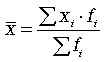
Так, нам необходимо рассчитать средний курс акций какого-то акционерного общества на торгах фондовой биржи.

Известно, что сделки осуществлялись в течение 5 дней (5 сделок), количество проданных акций по курсу продаж распределилось следующим образом:

1 — 800 ак. — 1010 руб.

2 — 650 ак. — 990 руб.

3 — 700 ак. — 1015 руб.

4 — 550 ак. — 900 руб.

5 — 850 ак. — 1150 руб.

Исходным соотношением для определения среднего курса стоимости акций является отношение общей суммы сделок (ОСС) к количеству проданных акций (КПА):

ОСС = 1010 · 800 + 990 · 650 + 1015 · 700+900·550+1150·850= 3 634 500;

В этом случае средний курс стоимости акций был равен:

Необходимо знать свойства арифметической средней, что очень важно как для ее использования, так и при ее расчете. Можно выделить три основных свойства, которые наиболее всего обусловили широкое применение арифметической средней в статистико-экономических расчетах.

Свойство первое (нулевое): сумма положительных отклонений индивидуальных значений признака от его среднего значения равна сумме отрицательных отклонений. Это очень важное свойство, поскольку оно показывает, что любые отклонения (как с +, так и с -), вызванные случайными причинами, взаимно будут погашены.

Доказательство:

Свойство второе (минимальное): сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа (а), т.е. есть число минимальное.

Составим сумму квадратов отклонений от переменной а:

(5.4)

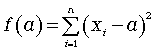
Чтобы найти экстремум этой функции, необходимо ее производную по а приравнять нулю:

(5.5)

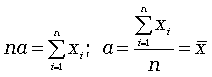
Следовательно, экстремум суммы квадратов отклонений достигается при 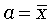. Этот экстремум — минимум, так как функция не может иметь максимума.

Свойство третье: средняя арифметическая постоянной величины равна этой постоянной: 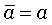при а = const.

Кроме этих трех важнейших свойств средней арифметической существуют так называемые расчетные свойства, которые постепенно теряют свою значимость в связи с использованием электронно-вычислительной техники:

если индивидуальное значение признака каждой единицы умножить или разделить на постоянное число, то средняя арифметическая увеличится или уменьшится во столько же раз;
средняя арифметическая не изменится, если вес (частоту) каждого значения признака разделить на постоянное число;
если индивидуальные значения признака каждой единицы уменьшить или увеличить на одну и ту же величину, то средняя арифметическая уменьшится или увеличится на ту же самую величину.

Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:

(5.6)

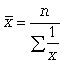
К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая — со скоростью 100 км/ч, вторая — 90 км/ч.

Применяя метод средней гармонической, мы вычисляем среднюю скорость:

В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид:

(5.7)

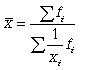
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.

Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров.

Допустим, необходимо узнать среднюю цену реализованных товаров:

Вид товара	Цена за единицу, руб.	Сумма реализаций, руб.
а
б
с

Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна:

Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.

Для простой средней геометрической:

Для взвешенной средней геометрической:

(5.9)

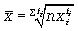
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Формула простой средней квадратической:

(5.10)

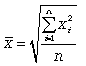
Формула взвешенной средней квадратической:

(5.11)

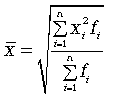
В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования.

Выбор средней предполагает такую последовательность:

а) установление обобщающего показателя совокупности;

б) определение для данного обобщающего показателя математического соотношения величин;

в) замена индивидуальных значений средними величинами;

г) расчет средней с помощью соответствующего уравнения.

Источник