Способы определения скорости звука

Способы определения скорости звука

Новый Эталон Килограмма

может в ближайшее время заменить устаревший платиново-иридиевый. »»»

Солнце Становится Ближе

получены изображения высокого разрешения Солнца с космической обсерватории Solar Dynamics Observatory. »»»

Человек «Искрививший» Время

биография Альберта Эйнштейна — величайшего физика создавшего «Общую теорию относительности». »»»

Что за Очки у Будущего?

история создания, развития и будущее популярного оптического прибора. »»»

Непосредственно измерение скорости звука требует лишь двух замеров: расстояния источника от наблюдателя и времени, за которое звук покрывает это расстояние. Тогда скорость может быть подсчитана по формуле скорость = расстояние / время. В древности скорость звука измеряли, ставя пушку на одной стороне долины, а наблюдатель располагался на другой ее стороне. Замерялось расстояние между пушкой и наблюдателем.

Наблюдатель по часам отмечал время, прошедшее между появлением вспышки и моментом, когда был услышан звук. Временем, за которое свет проходил это расстояние, пренебрегали. Для того чтобы в наибольшей степени устранить влияние ветра, с каждой стороны было по пушке и наблюдателю и каждая пушка стреляла примерно в одно и то же время.

Бралось среднее значение двух замеров времени, и на его основании определялась скорость. Она оказалась примерно равной 340 мс -1 . Большим недостатком этого способа измерения было то, что не всегда пушка оказывалась под рукой!

Многие экзаменуемые описывают похожий способ. Один ученик стоит на одной стороне футбольного поля состартовым пистолетом, а другой — на другой его стороне с секундомером. Расстояние между ними тщательно измеряется рулеткой. Ученик пускает секундомер, когда видит, как из ствола появляется дымок, и останавливает его, услышав звук. То же самое проделывается, когда они поменяются местами, чтобы компенсировать воздействие ветра. Затем определяется среднее время.

Поскольку звук распространяется со скоростью 340 мс -1 , то секундомер, скорее всего, не будет достаточно точен. Предпочтительнее оперировать сантисекундами или миллисекундами.

Измерение скорости звука с помощью эха

Когда произведен короткий резкий звук, например хлопок, то волновой импульс может быть отражен крупным препятствием, например стеной, и услышан наблюдателем. Этот отраженный импульс называется эхом. Представим, что на расстоянии 50 м от стены стоит человек и производит один хлопок. Когда эхо услышано, звук прошел 100 м. Измерение этого интервала секундомером не будет достаточно точным. Вместе с тем если второй человек держит секундомер, а первый хлопает, то время для большого числа звуков эха может быть получено с достаточной точностью.

Предположим, что расстояние, на котором хлопающий человек находится перед стеной, составляет 50 м, а временной интервал между первым и сто первым хлопком составляет 30 с, тогда:

скорость звука = пройденное расстояние / время одного хлопка = 100м : 30 /₁₀₀с = 333 мс -1

Измерение скорости звука с помощью осциллографа

Более сложным способом прямого измерения скорости звука является применение осциллографа. Громкоговоритель испускает импульсы через равные интервалы, и они фиксируются катодно-лучевым осциллографом (см. рис.). Когда импульс получен микрофоном, он также будет зарегистрирован осциллографом. Если известны временные характеристики осциллографа, то может быть найден временной интервал между двумя импульсами.

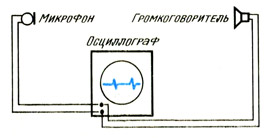
Замеряется расстояние между громкоговорителем и микрофоном. Скорость звука может быть найдена по формуле скорость = расстояние / время.

Скорость звука в различных средах

Скорость звука выше в твердых телах, чем в жидкостях, и выше в жидкостях, чем в газах. Проведенные в прошлом эксперименты на Женевском озере показали, что скорость звука в воде значительно выше, чем в воздухе. В пресной воде скорость звука составляет 1410 мс -1 , в морской воде — 1540 мс -1 . В железе скорость звука составляет примерно 5000 мс -1 .

Посылая звуковые сигналы и отмечая временной интервал до прихода отраженного сигнала (эха), можно определить глубину моря и местонахождение косяков рыбы. Во время войны эхолоты высокочастотного звука применялись для обнаружения мин. Летучие мыши в полете используют особую форму эхосигнала для обнаружения препятствий. Летучая мышь испускает высокочастотный звук, который отражается от объекта на ее пути. Мышь слышит эхо, определяет местонахождение объекта и уклоняется от него.

Скорость звука в воздухе зависит от атмосферных условий. Скорость звука пропорциональна квадратному корню из частного от деления давления на плотность. Изменения давлении не влияют на скорость звука в воздухе. Это связано с тем, что увеличение давления влечет за собой соответствующее увеличение плотности и отношение давления к плотности остается постоянным.

На скорость звука в воздухе (как и в любом газе) влияют изменения температуры. Законы для газов указывают, что отношение давления к плотности пропорционально температуре по Кельвину. Таким образом, скорость звука пропорциональна √T. Звуковой барьер легче преодолевать на больших высотах, потому что там ниже температура.

На скорость звука влияют изменения влажности. Плотность водяного пара меньше плотности сухого воздуха при одинаковом давлении. Ночью, когда влажность повышается, звук распространяется быстрее. Звуки слышны более ясно тихой туманной ночью.

Это происходит частично вследствие повышенной влажности, а частично из-за того, что в этих условиях обычно имеет место температурная инверсия, при которой звуки преломляются таким образом, что они не рассеиваются.

Источник

Скорость звука

Из Википедии — свободной энциклопедии

Скорость звука в различных средах [1]

0 °C, 101325 Па	м/с	км/ч
Азот	334	1202,4
Аммиак	415	1494,0
Ацетилен	327	1177,2
Водород	1284	4622,4
Воздух	331	1191,6
Гелий	965	3474,0
Кислород	316	1137,6
Метан	430	1548,0
Угарный газ	338	1216,8
Неон	435	1566,0
Углекислый газ	259	932,4
Хлор	206	741,6
Жидкости
Вода	1403	5050,8
Ртуть	1383	4978,0
Твёрдые тела
Алмаз	12000	43200,0
Железо	5950	21420,0
Золото	3240	11664,0
Литий	6000	21600,0
Стекло	4800	17280,0

Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).

Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.

Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.

Источник

—> Детская Энциклопедия —>

Как измерили скорость звука

Мысль измерить скорость звука впервые пришла английскому философу Фрэнсису Бэ­кону. По его совету этим занялся француз­ский ученый Марен Марсенн. В 1630 г. он про­вел наблюдение над выстрелом из мушкета. Расстояние между наблюдателем и мушкетом было поделено на время, прошедшее между вспышкой от выстрела и долетевшим до наблю­дателя звуком. Марсенн нашел, что скорость звука равна 230 туазам в секунду, что соответ­ствует 448 м/сек.

Спустя полвека английский ученый Исаак Ньютон вычислил скорость звука теоретически, исходя из упругих свойств воздуха и за­висимости объема газа от давления, зависимости, выраженной законом Бойля—Мариотта. Эта скорость оказалась немногим более половины скорости, полученной в опыте Марсенна. Когда теория противоречит опыту, следует искать, где же ошибка. Ее начали искать и в теорети­ческих рассуждениях Ньютона, и в опыте Марсенна.

В 1738 г. французская Академия наук по­вторила измерение скорости звука. Опыт был поставлен на холме Монмартр, близ Парижа. Было установлено, что скорость звука равна 171 туазу в секунду, что соответствует 337 м/сек. Несовпадение с опытом Марсенна объяснили тем, что его измерение времени было несовершенным. Однако и результат по­вторного опыта не соответствовал теоретиче­ской формуле Ньютона.

В 1808 г. французский ученый Пуассон выяснил, что закономерность, обнаруженная Бойлем и Мариоттом (именно она была поло­жена в основу расчетов Ньютона), неприме­нима для описания, как распространяется звук в воздухе. Этот закон справедлив лишь в том случае, когда объем газа изменяется медленно — так, что сжимаемый газ отдает среде, которая его окружает, возникающее в нем тепло; или, нао­борот, так, что медленно расширяющийся газ успевает нагреваться от окружающей среды. Следовательно, постоянство температуры воз­духа (основное условие закона Бойля—Мариот­та) может быть сохранено лишь в изотермиче­ских условиях, т. е. при свободном теплообмене между сжимаемым газом и окружающей этот газ средой.

Именно этих условий и нет в звуковой волне. Теплопроводность воздуха мала, а расстояние между слоями сжатия и разрежения велико. Избыток тепла из слоя сжатия не успевает пе­рейти в слой разрежения. Давление и объем изменяются в соседних слоях без теплообмена и, следовательно, при изменяющейся темпе­ратуре. Физические процессы, происходящие без теплообмена с окружающей средой, назы­ваются адиабатическими. В адиабатическом процессе сжимаемый газ нагревается (вспом­ните, как нагревается велосипедный насос, если очень быстро накачивать шину), а рас­ширяющийся — охлаждается.

Различие между расширениями газа в изо­термических и адиабатических условиях позво­лило французскому ученому Лапласу объяснить, почему скорость звука, вычисленная по формуле Ньютона, не совпадает с результатом опыта: колебания звукового давления в воздухе про­исходят в адиабатических, а не в изотермиче­ских условиях.

В 1822 г. близ Парижа вновь были постав­лены опыты. В них участвовали ученые: Гей-Люссак, Араго, Гумбольдт и др. Результаты опыта совпали с теоретическими вычислениями Лапласа и подтвердили, что скорость зву­ка возрастает с повышением температуры. В су­хом воздухе при 0°Ц она равна 331,5 м/сек, а при 20°Ц — 344 м/сек.

При одной и той же температуре скорость звука больше в том газе, у которого меньше молекулярный вес. При 0°Ц скорость звука:

в водороде — 1284 м/сек,

в гелии — 965 м/сек,

в азоте — 334 м/сек,

в кислороде— 316 м/сек.

В воде, упругость которой больше, чем у воз­духа, звук распространяется при 20°Ц со ско­ростью 1484 м/сек. Упругость твердых тел боль­ше, чем жидкости. В алюминии, железе, стали скорость звука равна примерно 5000 м/сек.

Источник

Способы определения скорости звука

Лабораторная работа № 1

Определение скорости звука методом сдвига фаз

Цель работы : определить скорость звука методом сдвига фаз.

Приборы и оборудование : звуковой генератор, электронный осциллограф, микрофон, динамический громкоговоритель, измерительная линейка.

Краткая теория и метод измерений

Звук представляет собой колебания упругой среды, воспринимаемые нашими органами слуха. Ухо человека воспринимает колебания определенной частоты и интенсивности, поэтому колебания, частота которых лежит в пределах от 16 до 20000 Гц и которые могут быть восприняты ухом, называются звуковыми.

Физиологическое восприятие звука является отражением соответствующих физических его характеристик. Так, гармоническое колебание определенной частоты воспринимается нами как определенный музыкальный тон. Физической характеристике – частоте колебаний – соответствует физиологическое понятие – высота звука. Малые частоты колебаний вызывают ощущение так называемого низкого тона (бас, баритон). Большие частоты колебаний вызывают ощущение звука высокого тона (сопрано, дискант). Чем больше колебаний, тем больше высота тона воспринимаемого звука.

Сила звука является физической характеристикой интенсивности звуковых колебаний. Мы оцениваем ее субъективно как громкость звука.

Для возникновения и распространения звуковых волн необходимо наличие упругой среды (твердое тело, воздух, вода). Возникновение волн возможно, если среда оказывает упругое сопротивление деформациям и обладает инерцией. Твердое тело оказывает сопротивление деформациям как продольным – растяжению и сжатию, так и сдвигу. Поэтому в твердом теле звуковые волны могут быть и продольные, и поперечные. В жидкостях и газах, которые не оказывают в обычных условиях сопротивления сдвигу, звуковые волны только продольные.

Многочисленные измерения скорости звука в различных газообразных и однородных твердых телах показывают, что она не зависит от частоты. Наибольшие скорости звука в твердых телах, наименьшие – в газах. Скорость звука в твердых телах для продольных и поперечных волн различаются.

При распространении звуковых волн в обычных условиях мы имеем довольно сложную картину. Звуковые волны, встречая препятствие, легко огибают его в тех случаях, когда длина волны много больше размеров препятствия, и отражаются от него примерно так же, как свет, если длина волны много меньше размеров препятствия.

При отражении звука от горы, стены и других значительных препятствий можно наблюдать, что угол падения волны равен углу отражения. В тех случаях, когда размеры препятствия сравнимы с длиной волны, законы распространения звуковой волны около препятствий становятся более сложными, имеет место и некоторое отражение и огибание (дифракция), как около небольших (по сравнению с длиной волны) препятствий.

Т.к. звуковые волны относятся к продольным механическим волнам, они характеризуются теми же величинами, что и механические волны: частотой n , периодом колебаний T, амплитудой A, начальной фазой колебания j _o , длиной волны l .

Для звуковой волны длиной l и частотой n , как и для любого волнового процесса, скорость определяется по формуле:

= n l .

Следовательно, для измерения скорости звука достаточно определить длину звуковой волны в данной среде l и частоту n , как и для любого волнового процесса.

Для измерения этих характеристик воспользуемся акустической установкой, где излучатель и приёмник звука находятся на некотором расстоянии L друг от друга. Если излучаемое звуковое колебание может быть записано в виде:

то колебание, достигшее приёмника будет выражаться уравнением

= A sin ( w t — D j ),

где — сдвиг фазы.

Таким образом, звуковая волна, пройдя путь L от излучателя до приёмника, получает запаздывание по фазе. Отсюда следует, что

.

Если зафиксировать сдвиг фаз D j =2 p n , то из (1) и (4) видно, что этот сдвиг фаз можно получить:

а) при всех значениях L кратных l :

,

б) при постоянном расстоянии между источником и приемником, но различных частотах n :

,

( n=1, 2, 3, .).

Отсюда можно сделать вывод, что скорость звука можно определить по величине сдвига фаз, обусловленного или изменением расстояния L между источником и приемником при n =const, или изменением частоты n волны при L=const:

.

Описание экспериментальной установки

От звукового генератора электромагнитные колебания звуковой частоты подаются одновременно на вертикальные пластины осциллографа, отклоняющие электронный луч по горизонтали и на горизонтальные пластины, отклоняющие электронный луч по вертикали. При этом на вертикальные пластины колебания подаются непосредственно, а сигналы, подаваемые на горизонтальные пластины, попадают вначале на динамический громкоговоритель ДГ, преобразуются в механические (звуковые колебания) той же частоты, затем, пройдя путь от громкоговорителя до микрофона и превращаясь в последнем в колебания тока той же частоты, подаются на горизонтальные пластины осциллографа. Сдвиг по времени происходит в результате прохождения звуковых колебаний от громкоговорителя до микрофона. В результате воздействия этих двух взаимно перпендикулярных гармонических колебаний на луч осциллографа на экране должно получиться изображение эллипса.

Рассмотрим этот процесс. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях с одинаковыми периодами. За направление колебаний взяты оси ОХ и ОУ. Тогда уравнение колебаний будет:

где A₁ и A₂, j ₀₁ и j ₀₂ — соответствующие амплитуды и начальные фазы первого и второго колебаний.

В результате простейших преобразований из уравнений (7) находим уравнение траектории в следующем виде:

.

Это уравнение представляет уравнение эллипса, характеристики которого определяются значением разности фаз ( j ₂ — j ₁ ).

Рассмотрим частные случаи:

а) Пусть разность фаз ( j ₂ — j ₁ ) слагаемых колебаний равна нулю, т.е. j ₁₌ j ₂₌ j . Уравнение траектории (8) в этом случае примет следующий вид:

или .

.

Мы получили уравнение прямой, проходящей через начало координат и образующей с осью ОХ угол, тангенс которого равен (рис. 2). По этой прямой точка совершает гармоническое колебание, при этом период результирующего колебания равен периоду слагаемых колебаний, а амплитуда результирующего колебания равна: .

б) Предположим теперь, что разность фаз ( j ₂ — j ₁ ) слагаемых колебаний равна p , т.е. ( j ₂ — j ₁ )= p . Уравнение траектории в этом случае примет вид:

,

.

Это уравнение представляет собой уравнение прямой, расположенной, как показано на рис. 3. По этой прямой точка совершает гармоническое колебание с той же амплитудой, что и в предыдущем случае.

в) Если разность фаз ( j ₂ — j ₁ ) слагаемых колебаний равна или , то уравнение траектории имеет вид:

.

Это уравнение эллипса относительно осей ОХ и ОУ (рис. 4).

Все прочие значения разности фаз, кроме или , дают эллипс, не приведенный к осям ОХ и ОУ. Некоторые из возможных видов траекторий, возникающих при сложении взаимно перпендикулярных гармонических колебаний одного периода, изображены на рис.5.

Прямые на рис. 2 и 3 следует рассматривать как вырожденный эллипс. Из приведенного примера следует, что движение точки по эллипсу также может быть разложено на два взаимно перпендикулярных колебания, разность между которыми определяется видом эллипса и направлением движения точки.

Фаза колебаний, поступающих от генератора (излучателя) на ОХ пластины осциллографа, всё время одинакова. Фаза же колебаний, достигающих микрофона и попадающих на ОУ пластины осциллографа, меняется периодически при изменении частоты излучателя n (при L=const) либо при изменении расстояний между излучателем и приемником при n =const.

Изменение разности фаз колебаний, подаваемых на пластины осциллографа при изменении либо L, либо n приводит к изменению формы и положения эллипса на экране. При условии постоянства амплитуды колебаний во время опыта и отсутствия нелинейности искажений картина на экране такова: при некотором расстоянии L при j =0 на экране эллипс вырождается в прямую, проходящую в первом и третьем (во втором и четвёртом) в квадрантах координатной сетки экрана осциллографа. Одну из этих прямых обычно принимают за начальную точку отсчёта. При перемещении динамика на прямая переходит в эллипс, который вращается около нулевой точки координатной оси и опять переходит в прямую, но проходящую уже через второй и четвёртый или первый и третий квадрант. Если изменить D L ещё на (т.е. уже D L = l ), то на экране получится прежняя картина (прямая, проходящая через 1 и 3 или 2 и 4 квадранты). Аналогичное изменение картины на экране осциллографа можно получить, изменяя частоту генератора n при расстоянии L=const между динамиком и микрофоном.

Задание 1. Определение скорости звука изменением расстояния между излучателем и динамиком

1. Включив звуковой генератор и установив любую частоту в пределах от 2000 Гц до 13000 Гц, получите на экране осциллографа эллипс.

2. Изменением расстояния между динамиком и микрофоном превратите в прямую, проходящую через 1 и 3 или через 2 и 4 квадранты. Определите начальное расстояние между микрофоном и динамиком L _нач .

3. Перемещайте динамик от начальной точки навстречу микрофону или от него. При n =const наблюдайте периодическое изменение картины на экране осциллографа. Определите при этом число полных периодов изменения картины n.

4. Определите конечное расстояние между микрофоном и динамиком L_кон.

5. Вычислите длину волны звука по соотношению , так как одно полное изменение картины на экране осциллографа соответствует изменению на длину волны l .

6. Проведите подобные измерения для 3-5 разных значений частот (2 кГц-13 кГц) в пределах 10 cм L

7. По формуле (2) рассчитайте скорость звука. Результаты измерений занесите в табл. 1.

Источник