Способы определения расстояния до звезд перечислить

Как определить расстояние до звёзд

Смотря на мерцающее ночное небо, нам кажется, что расстояние до звёзд не такое уж большое. А сами они малюсенькие точки во Вселенной. Однако это лишь видимость.

По правде говоря, маленькими светила не назовёшь, а дистанция между нами, как громадная пропасть. Кроме того, расстояние между самими звездами также неимоверно огромное. Разумеется, для нашего понимания, но не для космического пространства.

В древние времена люди считали, что все небесные тела одинаково удалены друг от друга. Но благодаря изучению космоса, со временем, взгляды изменились.

звёзды в космосе

В чём измеряется расстояние между звездами

Действительно, интересно какими единицами астрономы измеряют расстояние до звезд?
На самом деле, расстояние до звезд, как и до любых других космических тел, измеряется не в привычных нам километрах, а в световых годах или парсеках.

Световой год подразумевает пройденное световым лучом расстояние за один год, при условии, что его скорость равна 300 тысяч км в секунду. Только представьте, один световой год соответствует 9,5 миллионам миллионов километров.

Применение метров и километров при определении дистанций между звездами и расстоянии от Земли до них, очень-очень сложно и проблематично.

Хотя часто степень удалённости астрономических объектов настолько велик, что использование световых лет также неудобно. Поэтому для сокращения используют такую единицу измерения как парсек. Он равняется 3,26 светового года.

Помимо этого, за единицу измерения могут использовать мегапарсек, который в один миллион раз больше обычного (то есть составляет 3 260 000 световых лет).

Летящая звезда

Методы и способы определения расстояния до звезд

Всегда и во всём человек ищет свойства, характеристики и отличительные черты. На сегодняшний день, мы способны рассчитать любой отрезок, применяя практические и теоретические приёмы.

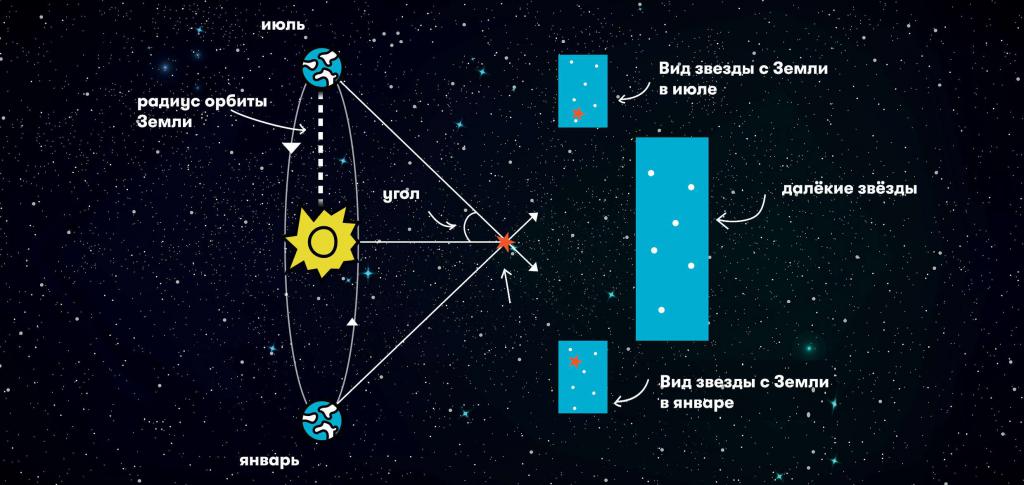
А вот как определяют расстояние до звезд? Для этого чаще всего используют метод параллакса.

Параллакс — это изменение видимого положения объекта в отношении удалённого фона, которое напрямую зависит от положения наблюдателя.

В случае определения расстояния до звезд, наблюдение проводят с двух сторон от Солнца на протяжении 6 месяцев друг от друга. В результате полученное смещение светила даёт возможность оценивать дистанцию до него.

Если бы звёздное тело было бы удалено от нашей планеты на 3,26 световых года или на 1 парсек, то его параллакс составлял бы 1 секунду дуги. Но, наверное, к счастью, нет ни одного настолько близко расположенного звёздного тела к нам.

расстояние до звезды

Другие способы определения расстояния до звёзд

Конечно, существуют и другие подходы. Так, например, определить расстояние до звезд можно с помощью фотометрического метода. При нём измеряют освещённость, которая возникает одинаковыми по силе и мощности источниками. Именно полученное значение освещённости обратно пропорциональна квадратам до удалённости тел друг от друга.

Определение расстояний до звезд возможно методом анализа спектра объектов. Для этого проводится исследование химического состава и физических характеристик, а также изучение спектров тела.

Итак, мы узнали в каких единицах измеряется и как определяют расстояние до звёзд.

Как известно, Солнце является самой близкой к нам звездой. Поэтому часто путь к нему указывают в км (149,6 млн км), что в переводе на световые года равно 8,3 световой минуте.

Расстояние между звездами и планетами нашей Солнечной системы имеет внушительные показатели. Например, степень удалённости планеты Плутон от Земли равна приблизительно 5 световым часам, а следующее близлежащее к нам светило (Проксима Центавра) располагается на расстоянии 4,2 световых года.

Представляете, сколько уже известно и доступно для нас, а сколько ещё предстоит узнать про нашу Вселенную!

Проксима Центавра (одна из самых маленьких звёзд)

Источник

Методы определения расстояний до звёзд. конецформыначалоформы

Метод параллакса. Вследствие годичного движения Земли по орбите близкие звезды немного перемещаются относительно далеких «неподвижных» звезд. За год такая звезда описывает на небесной сфере малый эллипс, размеры которого тем меньше, чем звезда дальше. В угловой мере большая полуось этого эллипса приблизительно равна величине максимального угла, под каким со звезды видна 1 а. е. (большая полуось земной орбиты), перпендикулярная направлению на звезду. Этот угол (), называемый годичным или тригонометрическим параллаксом звезды, равный половине ее видимого смещения за год, служит для измерения расстояния до нее на основе тригонометрических соотношений между сторонами и углами треугольника , в котором известен угол и базис — большая полуось земной орбиты. Расстояние r до звезды, определяемое по величине ее тригонометрического параллакса , равно: r = 206265»/ (а. е.), где параллакс выражен в угловых секундах.конецформыначалоформы Для удобства определения расстояний до звезд с помощью параллаксов в астрономии применяют специальную единицу длины — парсек (пс). Звезда, находящаяся на расстоянии 1 пс, имеет параллакс, равный 1». Согласно вышеназванной формуле, 1 пс = 206265 а. е. = 3,086·1018 см.

Фотометрический метод определения расстояний. Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т. е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояния до них. Выражение освещенностей в звездных величинах (m — видимая звездная величина, М — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф (пс): lgrф = 0,2 (m — M) + 1. При определении rф по вышеназванной формуле погрешность составляет

30%. Для светил, у которых известны тригонометрические параллаксы, можно, определив М по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств. Зная расстояния до некоторого числа звезд, вычисленные методом параллакса, можно было вычислить светимости и сопоставить их со спектром тех же звезд. Точность определения расстояния таким способом составляет

Определение расстояния по относительным скоростям. Косвенным показателем расстояния до звезд являются их относительные скорости: как правило, чем ближе звезда, тем больше смещается она по небесной сфере. Определить таким способом расстояние, конечно нельзя, но этот способ дает возможность “вылавливать” близкие звезды. Также существует другой метод определения расстояний по скоростям, применимый для звездных скоплений. Он основан на том, что все звезды, принадлежащие одному скоплению, движутся в одном и том же направлении по параллельным траекториям. Измерив лучевую скорость звезд с помощью эффекта Доплера, а также скорость, с которой эти звезды смещаются относительно очень удаленных, то есть условно неподвижных звезд, можно определить расстояние до интересующего нас скопления.

Цефеиды. Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Цефеиды — это неустойчивые звезды спектральных классов от F6 до G8, которые пульсируют в результате нарушения равновесия между силой тяжести и внутренним давлением, причем кривая изменения их параметров напоминает гармонический закон. С течением времени колебания ослабевают и затухают; Периоды различных цефеид от 1,5 часов до 45 суток. Все цефеиды — гиганты большой светимости, причем светимость строго зависит от периода по формуле: M = — 0,35 — 2,08 lg T.

Источник

Как определяют расстояние до звезд: методы и формулы

Расстояния до удаленных небесных объектов, например, звезд, недоступны для прямого измерения. Их вычисляют, опираясь на измеряемые параметры этих объектов, такие как блеск звезды или периодическое изменение ее координат. В настоящее время разработано несколько методов вычисления звездных расстояний, и каждый из них имеет свои границы применимости. Рассмотрим подробнее, как ученые определяют расстояние до звезд.

Использование параллакса

Параллаксом называют смещение наблюдаемого объекта относительно удаленного фона при изменении положения наблюдателя. Зная расстояние между точками наблюдения (базис параллакса) и величину углового смещения объекта, несложно рассчитать расстояние до него. Чем меньше величина смещения, тем дальше находится объект. Межзвездные расстояния огромны, и, чтобы увеличить угол, используют максимально большой базис – для этого измеряют положение звезды в противоположных точках земной орбиты. Этот метод называется звездным годичным параллаксом.

Теперь легко понять, как измеряют расстояние до звезд методом годичного параллакса. Оно вычисляется как одна из сторон треугольника, образованного наблюдателем, Солнцем и удаленной звездой, и равно r = a/sin p, где: r – расстояние до звезды, а – расстояние от Земли до Солнца и p – годичный параллакс звезды. Поскольку параллаксы всех звезд меньше 1 угловой секунды (1’’), синус малого угла можно заменить величиной самого угла в радианной мере: sin p ≈ p’’/206265. Тогда получаем: r = a∙206265/p’’, или, в астрономических единицах, r = 206265/p’’.

Единицы межзвездных расстояний

Понятно, что полученная формула неудобна, как и выражение колоссальных расстояний в километрах или астрономических единицах. Поэтому в качестве общепринятой единицы в звездной астрономии принят парсек («параллакс-секунда»; сокращенно – пк). Это расстояние до звезды, годичный параллакс которой равен 1 секунде. В этом случае формула принимает простой и удобный вид: r = 1/p пк.

Один парсек равен 206265 астрономических единиц или приблизительно 30,8 триллионов километров. В популярной литературе и статьях часто используется такая единица, как световой год – расстояние, которое за год проходят в вакууме электромагнитные волны, не испытывая влияния гравитационных полей. Один световой год равен около 9,5 триллиона километров, или 0,3 парсека. Соответственно, один парсек составляет приблизительно 3,26 светового года.

Точность параллактического метода

Точность измерения параллакса в наземных условиях в настоящее время позволяет определение расстояний до звезд не более 200 парсек. Дальнейшее повышение точности достигается путем наблюдений с использованием космических телескопов.

Так, европейский спутник «Гиппарх» (HIPPARCOS, был запущен в 1989 году) позволил, во-первых, увеличить это расстояние до 1000 пк, а во-вторых, существенно уточнить уже известные звездные расстояния. Европейский же спутник «Гайя», или «Гея» (Gaia, запущен в 2013 году), повысил точность измерений еще в на два порядка. С помощью данных «Гайя» астрономы как определяют расстояние до звезд в радиусе 40 килопарсек, так и надеются открыть новые экзопланеты. Космический телескоп им. Хаббла достигает сопоставимой с «Гайя» точности. Вероятно, она близка к предельной для оптических измерений.

Несмотря на это ограничение, тригонометрический годичный параллакс служит калибровочной основой для других методов определения расстояний до звезд.

Фотометрия. Понятие звездной величины

Фотометрия в астрономии занимается измерением интенсивности испускаемого небесным объектом электромагнитного излучения, в том числе и в оптическом диапазоне. На основе фотометрических параметров различными методами определяют расстояние как до звезд, так и до иных удаленных объектов, например, галактик. Одним из основных понятий, используемых в фотометрических методах, является звездная величина, или блеск (обозначается индексом m ).

Видимая, или относительная (для оптического диапазона — визуальная) звездная величина измеряется непосредственно по яркости звезды и имеет шкалу, в которой возрастание величины характеризует падение яркости (так сложилось исторически). Например, Солнце имеет видимую звездную величину –26,7 m , Сириус имеет величину –1,46 m , а ближайшая к Солнцу звезда Проксима Центавра – величину +11,05 m .

Абсолютная звездная величина – вычисляемый параметр. Он соответствует видимой звездной величине звезды, если бы эта звезда находилась на расстоянии 10 пк. Этот параметр связывает блеск объекта с расстоянием до него. У приведенных в качестве примера звезд абсолютная величина составляет: у Солнца +4,8 m , у Сириуса +1,4 m , у Проксимы +15,5 m . Расстояние этих звезд соответственно 0,000005, 2,64 и 1,30 парсека. Они различаются по очень важному астрофизическому параметру – светимости.

Спектры и светимость звезд

Астрономы называют светимостью L полную энергию, излучаемую звездой (либо другим объектом) в единицу времени, то есть мощность звезды. Светимость может быть выражена через абсолютную звездную величину, однако, в отличие от нее, не зависит от расстояния.

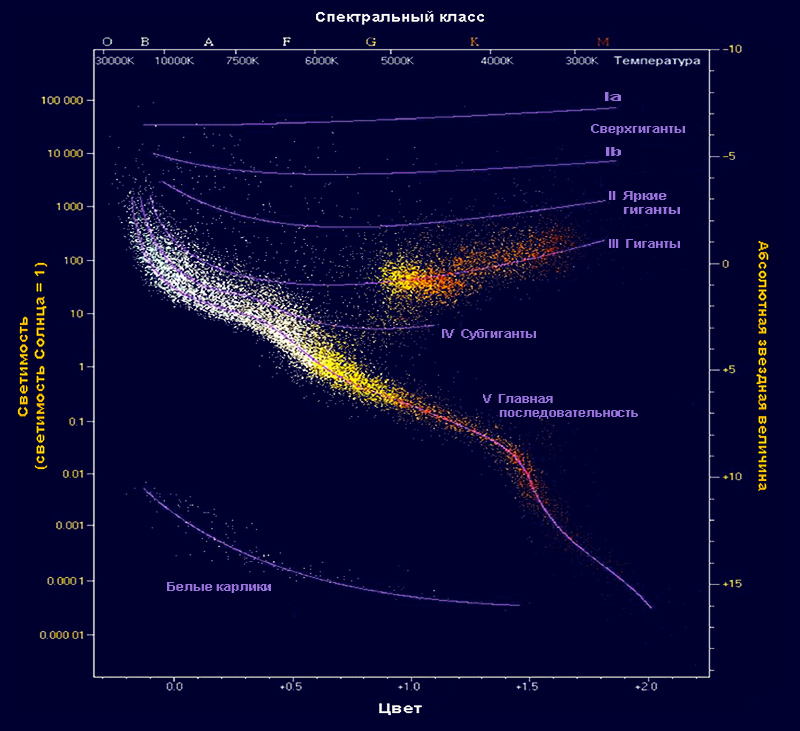
По спектру излучения, отражающему в первую очередь температуру (от нее зависит цвет), звезды подразделяются на несколько спектральных классов. Звезды одного спектрального класса характеризуются, как правило, одинаковой светимостью (здесь есть исключения, но они выявляются по особенностям спектра). Зависимость «спектр – светимость» (или «цвет – звездная величина») отображена на так называемой Диаграмме Герцшпрунга – Рассела.

Эта диаграмма дает возможность по спектральным классам звезд оценивать их абсолютные величины. А поскольку абсолютная величина связана несложным соотношением с расстоянием и с видимой, наблюдаемой величиной, далее нам уже ясно, как определяют расстояние до звезд. Формула имеет следующий вид: lg r = 0,2(m – M)+1. Здесь r – расстояние, m – видимая звездная величина и M – абсолютная величина. Точность такого метода невелика, но позволяет сделать оценку расстояния.

Стандартные свечи в астрономии

Существуют звезды, светимость которых характеризуется однозначным соответствием определенному физическому параметру. Благодаря этому астрономы с хорошей точностью по закону обратных квадратов определяют расстояние до звезд как функцию падения блеска. Чем меньше видимая величина такой звезды, тем дальше расположена сама звезда. К подобным объектам относятся, например, цефеиды и сверхновые типа Ia.

Цефеиды – переменные звезды, светимость которых строго связана с периодом пульсаций. Измерив блеск и период такой звезды, легко вычислить расстояние до нее. Цефеиды – очень яркие звезды. Современные телескопы способны разрешать цефеиды в других галактиках и таким образом установить расстояние до галактики.

Сверхновые типа Ia представляют собой взрывы определенного типа звезд в тесных двойных системах. Взрыв происходит при достижении звездой некоторого критического значения массы и всегда имеет одинаковую светимость и характер спада блеска, что также позволяет вычислить расстояние. Яркость сверхновых бывает сопоставима с яркостью целой галактики, поэтому с их помощью астрономы могут оценивать расстояния на очень больших, космологических масштабах – порядка миллиардов парсек.

Дальше всех

О самой близкой к нам звезде – Проксиме Центавра – знают многие. А вот какая из известных ныне звезд расположена дальше всех?

Самая дальняя звезда, принадлежащая к нашей Галактике, обнаружена не так давно. Она находится за пределами спирального диска Млечного Пути, на внешней границе галактического гало, на расстоянии около 122 700 пк, или 400 000 световых лет, в созвездии Весов. Это красный гигант 18-звездной величины. Конечно, известны и более далекие звезды, однако трудно установить точно их принадлежность к нашей Галактике.

Ну, а какая звезда из всех известных во Вселенной наиболее удалена от нас? Она имеет романтическое имя MACS J1149+2223 Lensed Star-1, или просто LS1, и расположена в 9 миллиардах световых лет. Ее обнаружение – это астрономическая удача, поскольку увидеть звезду на таком расстоянии оказалось возможно лишь благодаря событию гравитационного микролинзирования в далекой галактике, в свою очередь линзируемой более близким скоплением галактик. При этом использовался иной метод вычисления расстояния – по космологическому красному смещению. Этим способом определяют расстояния до самых удаленных объектов Вселенной, которые невозможно разрешить на отдельные звезды. И LS1 – один из самых удивительных и красивых примеров того, как определяют расстояния до звезд астрономы.

Источник