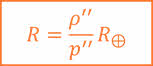- БИЛЕТ № 6. Способы определения расстояний до тел Солнечной системы и их размеров
- Способы определения расстояний до тел Солнечной системы и их размеров.
- Способы определения расстояния до тел солнечной системы их размеров
- Определение расстояний и размеров тел в Солнечной системе
- Урок 14. Астрономия 11 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Определение расстояний и размеров тел в Солнечной системе»
БИЛЕТ № 6. Способы определения расстояний до тел Солнечной системы и их размеров
- Способы определения расстояний до тел Солнечной системы и их размеров.
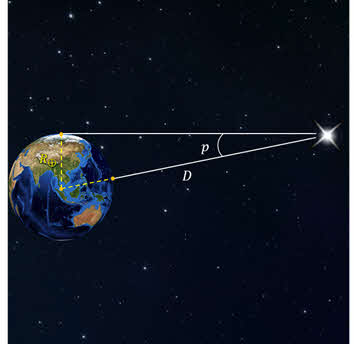
Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения.
p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила.
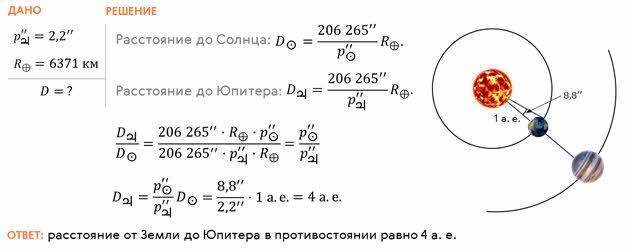
Радиолокационный метод.Он заключается в том, что на небесное тело посылают мощный кратковременный импульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние.
Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.
Лазерная локация Луны.Вскоре после изобретения мощных источников светового излучения — оптических квантовых генераторов (лазеров) — стали проводиться опыты по лазерной локации Луны. Метод лазерной локации аналогичен радиолокации, однако точность измерения значительно выше. Оптическая локация дает возможность определить расстояние между выбранными точками лунной и земной поверхности с точностью до сантиметров.
Для определения размеров Земли определяют расстояние между двумя пунктами, расположенными на одном меридиане, затем длину дуги l, соответствующей 1° —n.
Для определения размеров тел Солнечной системы можно измерить угол, под которым они видны земному наблюдателю – угловой радиус светила r и расстояние до светила D.
Учитывая p0 – горизонтальный параллакс светила и, что углы p0 и r малы,
- Определение светимости звезды на основе данных о ее размерах и температуре.
Источник
Способы определения расстояний до тел Солнечной системы и их размеров.



Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения.
p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила.
Радиолокационный метод.Он заключается в том, что на небесное тело посылают мощный кратковременный импульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние.
Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.
Лазерная локация Луны.Вскоре после изобретения мощных источников светового излучения — оптических квантовых генераторов (лазеров) — стали проводиться опыты по лазерной локации Луны. Метод лазерной локации аналогичен радиолокации, однако точность измерения значительно выше. Оптическая локация дает возможность определить расстояние между выбранными точками лунной и земной поверхности с точностью до сантиметров.
Для определения размеров Земли определяют расстояние между двумя пунктами, расположенными на одном меридиане, затем длину дуги l, соответствующей 1° —n.
Для определения размеров тел Солнечной системы можно измерить угол, под которым они видны земному наблюдателю – угловой радиус светила r и расстояние до светила D.
Учитывая p0 – горизонтальный параллакс светила и, что углы p0 и r малы,
3. Оборудование: стеклянная пластина, булавки, линейка, транспортир. Вывод согласно измерениям.
Источник
Способы определения расстояния до тел солнечной системы их размеров
§ 11. ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ ДО ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ И РАЗМЕРОВ ЭТИХ НЕБЕСНЫХ ТЕЛ
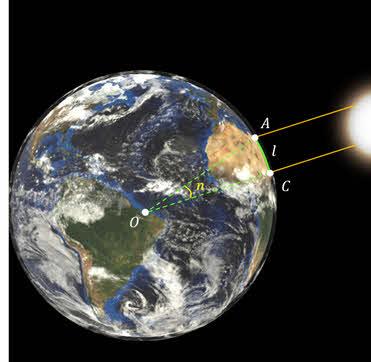
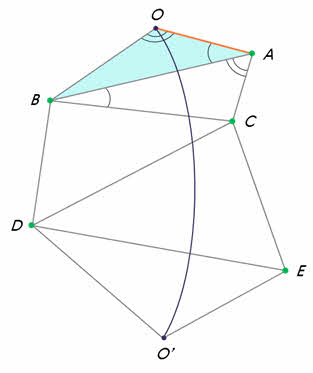
1. Определение расстояний по параллаксам светил. Допустим, что из точки А нужно определить расстояние до недоступной точки С (рис. 24). Для этого прежде всего тщательно измеряется расстояние до какой-нибудь доступной точки В. Отрезок АВ называется базисом. Далее из точек А и В угломерным геодезическим инструментом измеряют 

 |  |
 |
 |

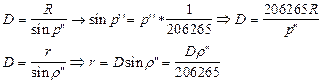
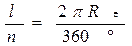
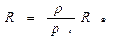





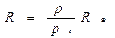
 (19)
(19) — экваториальный радиус Земли (сущность способа определения радиуса Земли будет изложена в § 12); р0 — горизонтальный параллакс светила.
— экваториальный радиус Земли (сущность способа определения радиуса Земли будет изложена в § 12); р0 — горизонтальный параллакс светила. = 8,79′). Поскольку углы р0 малы, то их синусы можно заменить самими углами, т.е. sin р0 ≈ р0, если величина угла выражена в радианах. Но р0 обычно выражено в секундах дуги, поэтому
= 8,79′). Поскольку углы р0 малы, то их синусы можно заменить самими углами, т.е. sin р0 ≈ р0, если величина угла выражена в радианах. Но р0 обычно выражено в секундах дуги, поэтому  так как 1 радиан = 57,3° = 3438′ = 206265′. Учитывая это, формулу (19) можно записать в виде:
так как 1 радиан = 57,3° = 3438′ = 206265′. Учитывая это, формулу (19) можно записать в виде: (20)
(20) — либо в километрах (если
— либо в километрах (если  — в километрах), либо в радиусах Земли.
— в километрах), либо в радиусах Земли.
 = 8,7940′.
= 8,7940′. , измеряют линейное ( l , например, в километрах) и угловое ( n , например, в градусах) расстояния между двумя пунктами земной поверхности, расположенными на одном географическом меридиане (рис. 26). Затем вычисляют длину дуги, соответствующую 1° этого меридиана, а потом и радиус Земли. Пусть l — длина дуги АВ, а центральный угол, опирающийся на эту дугу и равный разности географических широт точек А и В,
, измеряют линейное ( l , например, в километрах) и угловое ( n , например, в градусах) расстояния между двумя пунктами земной поверхности, расположенными на одном географическом меридиане (рис. 26). Затем вычисляют длину дуги, соответствующую 1° этого меридиана, а потом и радиус Земли. Пусть l — длина дуги АВ, а центральный угол, опирающийся на эту дугу и равный разности географических широт точек А и В,  AOB = п (О — центр Земли), тогда длина дуги 1° меридиана будет равна
AOB = п (О — центр Земли), тогда длина дуги 1° меридиана будет равна  а значит,
а значит, (21)
(21) (22)
(22) (22′)
(22′) и
и  малы, то
малы, то (23)
(23)




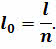
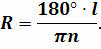

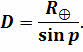
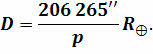

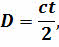
 .
.