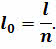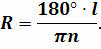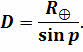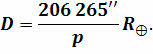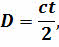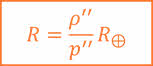Способы определения расстояния до планет солнечной системы

Урок 10

Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.

1 а.е. = 149 600 000 км

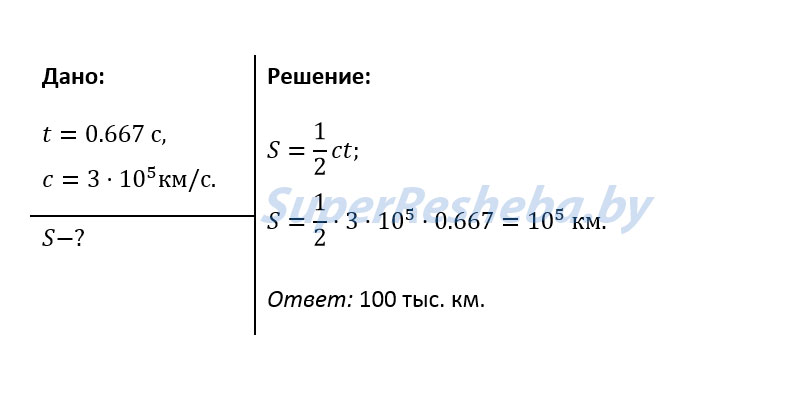
Расстояние до объекта по времени прохождения радиолокационного сигнала можно определить по формуле , где S = 1/2·ct, где S — расстояние до объекта, c — скорость света, t — время прохождения светила.

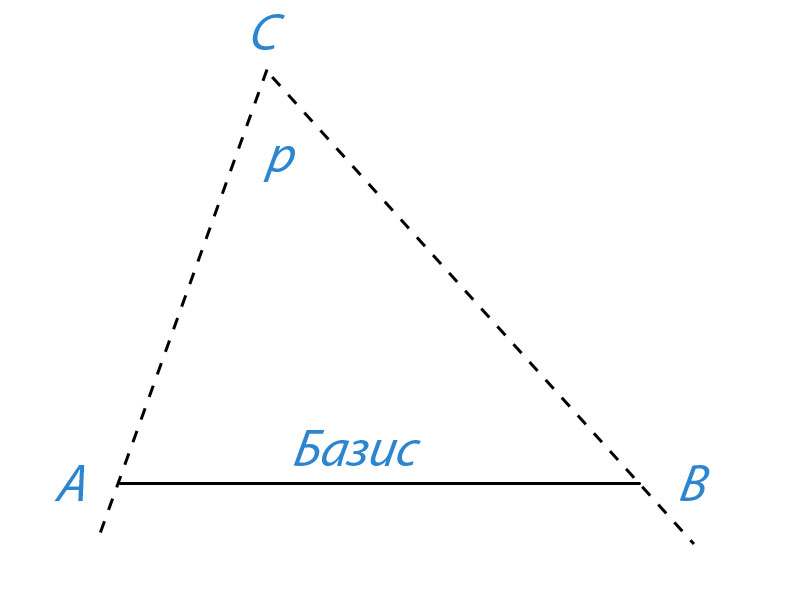
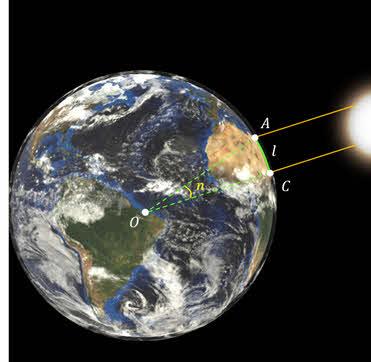
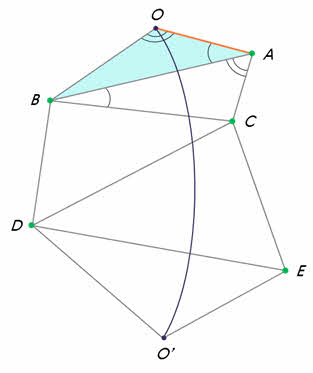
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.

Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.

По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.

r = D · sin(ρ); R = D · sin(ρ)/sin(p) · R; r = ρ/p · R.

1. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t — 0,667 с. На каком расстоянии от Земли находился в это время астероид?

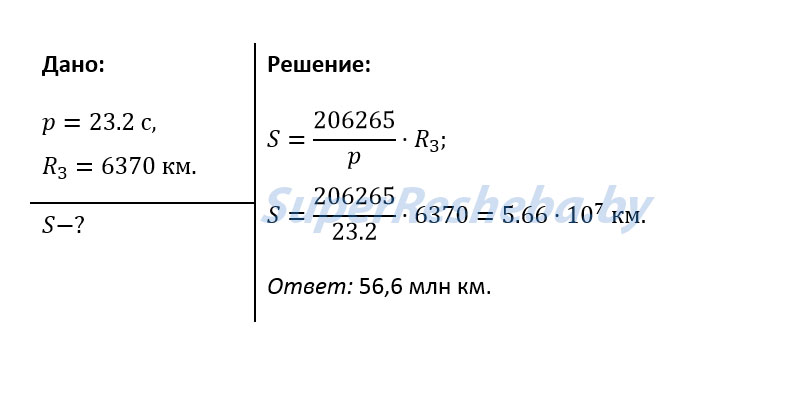
2. Определите расстояние от Земли до Марса во время великого противостояния, когда его горизонтальный параллакс p = 23,2″.

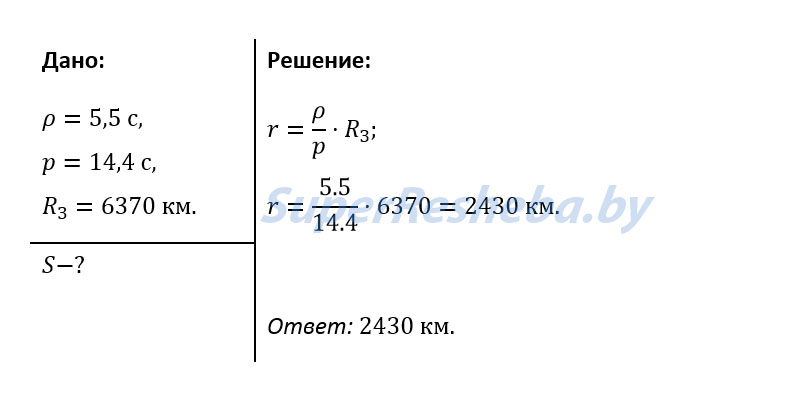
3. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус p = 5,5″, а горизонтальный параллакс p = 14,4″. Определите линейный радиус Меркурия.

1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?

Ответ: 41 млн км.

2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?

Ответ: 1,22 млн км.

3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.

Источник

Какие есть способы определения расстояний до тел Солнечной системы?

Способы определения расстояний до тел Солнечной системы и их размеров.

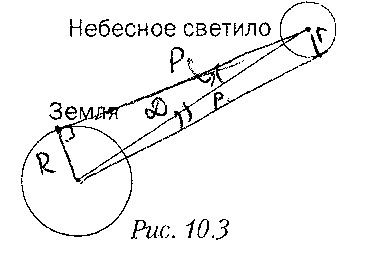
Сперва определяется расстояние до какой-нибудь доступной точки. Это расстояние называется базисом. Угол, под которым из недоступного места виден базис, называют параллаксом. Горизонтальным параллаксом называют угол, под которым с планеты виден радиус Земли, перпендикулярный лучу зрения.
p² – параллакс, r² – угловой радиус, R – радиус Земли, r – радиус светила.

Радиолокационный метод. Он заключается в том, что на небесное тело посылают мощный кратковременный им­пульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: известна. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние.

Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.

Лазерная локация Луны. Вскоре после изобретения мощных источников светового излучения — оптических квантовых генераторов (лазеров) — стали проводиться опыты по лазерной локации Луны. Метод лазерной локации анало­гичен радиолокации, однако точность измерения значи­тельно выше. Оптическая локация дает возможность опреде­лить расстояние между выбранными точками лунной и зем­ной поверхности с точностью до сантиметров.
Подробнее:

Источник

Как определить расстояние до планет и измерить размер Солнечной системы

Какого размера наша Солнечная система и где она кончается?

Как измерить расстояние до планеты?

В прошлом единственным методом измерения космических расстояний был метод горизонтального параллакса. Хотя этот метод достаточно точен и до сих пор применяется при расчете расстояния до очень далеких космических объектов, для измерения расстояний до планет-соседей по Солнечной системе, с середины 20-го века применяется более простой и ещё более точный способ – метод радиолокации.

В основе методики космической радиолокации лежит идея заимствованная у самой природы: достаточно просто найти на небесной сфере нужный объект (например, планету Венера), “прицелится” в неё и затем “выстрелить” радиоволнами сверхкороткого диапазона. Теперь нам остается только дождаться когда сигнал достигнет поверхности Венеры, отразится от неё и устремится обратно.

Скорость распространения радиоволн точно известна, а время между посылкой волн и их приемом также может быть измерено очень точно. Расстояние, покрытое радиоволнами за время путешествия туда и обратно, а следовательно, и расстояние до Венеры в заданный момент можно определить с несравненно большей точностью, чем методом параллаксов.

Начиная с 1961 г. года этот способ измерения близких космических расстояний стал основным. С помощью полученных данных было вычислено, что среднее расстояние от Земли до Солнца составляет 149 573 000 км.

Радиотелескопы без перерыва «сканируют» космос и ловят «эхо» своих сигналов отраженное от космических объектов

Световая секунда, световой год и другие космические единицы измерения

Используя кеплеровскую схему строения солнечной системы (Солнце в центре, планеты вращаются вокруг него), удобнее всего рассчитывать расстояния в пределах солнечной системы не от Земли, а от центра, то есть от Солнца. Но вот в каких единицах его отсчитывать?

• Во-первых, его можно выражать в миллионах километров. Километр — это наиболее распространенная единица для измерения больших расстояний.
• Во-вторых, чтобы избежать таких чисел, как миллионы километров, можно принять, что среднее расстояние от Земли до Солнца равно одной астрономической единице (сокращенно «а, е.») Тогда можно будет выражать расстояния в а, е., причем 1 а е. равна 149 500 000 км. С вполне достаточной точностью можно считать, что 1 а, е. равна 150 000 000 км.
• В-третьих, расстояние можно выразить через время, которое потребуется для того, чтобы его преодолел свет (или любое аналогичное излучение, например радиоволны). Скорость света в пустоте равна 299 776 км/сек. Число это можно для удобства округлить до 300 000 км/сек.

Таким образом, расстояние примерно в 300 000 км можно считать равным одной световой секунде (ибо это расстояние, преодолеваемое светом за одну секунду). Расстояние, в 60 раз большее, или 18 000 000 км, — это одна световая минута, а расстояние, еще в 60 раз большее, т.е. 1 080 000 000 км, — это один световой час.

Мы не слишком ошибемся, если будем считать, что световой час равен одному миллиарду километров.

Запомнив это, рассмотрим те планеты, которые были известны древним, и приведем таблицу их средних расстояний от Солнца, выраженных в каждой из трех указанных единиц.

Планеты	Среднее расстояние от Солнца
	миллионов км	астрономических единиц	световых часов
Меркурий	57,9	0,387	0,0535
Венера	108,2	0,723	0,102
Земля	149,5	1,000	0,137
Марс	227,9	1.524	0,211
Юпитер	778,3	5,203	0,722
Сатурн	1428,0	9,539	1,321

Уильям Гершель – в свое время раздвинул горизонты познания, открыв Уран и буквально удвоив границы Солнечной системы

Размеры Солнечной системы

В 17-м веке, когда был открыт Сатурн, астрономы считали его орбиту “границей” Солнечной системы, соответственно вся “система” умещалась в круг диаметром 3 миллиардов км.

Однако в 1781 г., когда английский астроном, немец по происхождению, Уильям Гершель (1738—1822) открыл планету Уран, диаметр Солнечной системы внезапно… удвоился!

А потом снова удвоился, когда сначала французский астроном Урбан Жозсф Леверье (1811 — 1877) открыл в 1846 г. Нептун, затем американский астроном Клайд Уильям Томбо (род. в 1906 г.) — Плутон в 1930 г.

Планеты	Среднее расстояние от Солнца
	миллионов км	астрономических единиц	световых часов
Уран	2872	19,182	2,63
Нептун	4498	30,058	4,26
Плутон	5910	39,518	5,47

Если мы рассмотрим орбиту Плутона, как ранее орбиту Сатурна, то увидим, что диаметр солнечной системы равен не 3, а 12 миллиардам километров. Лучу света, который преодолевает расстояние, равное окружности Земли, за 1 /₇ сек и пробегает от Земли до Луны за 1 1 /₄ сек, понадобится полдня для того, чтобы пересечь солнечную систему.

Кроме того, есть все основания считать, что вовсе не орбита Плутона отмечает границу владений Солнца. Это не значит, что мы должны предполагать существование еще не открытых более далеких планет (за исключением карликовых планет). Имеются уже известные небесные тела, которые время от времени очень легко увидеть и которые, без сомнения, уходят от Солнца гораздо дальше, чем Плутон на самой удаленной точке своей орбиты.

Где находятся границы Солнечной системы

В 1684 г. английский ученый Исаак Ньютон (1642—1727) открыл закон всемирного тяготения. Этот закон строго математически обосновал кеплеровскую схему строения солнечной системы и позволил вычислить орбиту тела, обращающегося вокруг Солнца, даже если тело наблюдалось лишь на части своей орбиты.

Это в свою очередь дало возможность приняться за кометы — небесные тела, которые время от времени появлялись на небе. В древности и в эпоху Средневековья астрономы считали, что кометы появляются без всякой правильности и что движение их не подчинено никаким естественным законам, широкие же массы были убеждены, что единственное назначение комет — предвещать несчастье.

Однако современник и друг Ньютона, английский ученый Эдмунд Галлей (1656—1742) попробовал применить к кометам закон тяготения. Он заметил, что некоторые особенно яркие кометы появлялись в небе через каждые 75—76 лет.

И вот в 1704 г. он предположил, что все эти кометы на самом деле были одним и тем же небесным телом, которое двигалось вокруг Солнца по постоянной эллиптической орбите, причем орбите настолько вытянутой, что значительная ее часть лежала на колоссальном расстоянии от Земли. Когда комета находилась вдали от Земли, она была невидима.

Но через каждые 75 или 76 лет она оказывалась на той части своей орбиты, которая расположена ближе всего к Солнцу (и к Земле), и вот тогда-то она становилась видимой.

Попытка запечатлеть реальные размеры и расстояния планет Солнечной системы от Солнца и друг от друга

Галлей вычислил орбиту этой кометы и предсказал, что она вновь вернется в 1758 г. И действительно, комета появилась в тот год (через 16 лет после смерти Галлея) и с тех пор получила название кометы Галлея.

В ближайшей к Солнцу точке своей орбиты комета Галлея оказывается от него всего лишь примерно в 90 000 000 км, заходя таким образом немного внутрь орбиты Венеры В наиболее же удаленной от Солнца части своей орбиты комета Галлея уходит от него приблизительно в 3 1 /₂ раза дальше, чем Сатурн.

Таким образом, к 1760 г. астрономы прекрасно знали, что солнечная система не очерчена орбитой “последней” планеты.

Более того, комета Галлея — одна из комет, относительно близких к Солнцу. Существуют кометы, которые движутся вокруг него по таким невероятно вытянутым орбитам, что возвращаются к нему только раз в несколько столетий, а то и тысячелетий. Они уходят от Солнца не на миллиарды километров, а скорее всего на сотни миллиардов.

Голландский астроном Ян Хендрик Оорт (род. в 1900 г) в 1950 г. высказал предположение, что, возможно, существует целое огромное облако комет (известное как “Облако Оорта”), которые на протяжении всей своей орбиты находятся так далеко от Солнца, что никогда не бывают видимы.

Отсюда следует, что максимальный диаметр солнечной системы может достигать 1000 миллиардов, т. е триллиона (1 000 000 000 000) километров или даже больше. Световому лучу требуется 40 суток, чтобы покрыть такое расстояние. Таким образом, можно сказать, что диаметр солнечной системы превосходит один световой месяц.

Источник

Определение расстояний и размеров тел в Солнечной системе

Урок 14. Астрономия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Определение расстояний и размеров тел в Солнечной системе»

Вы уже знаете, что ещё в Древней Греции учёными и мыслителями было установлено, что наша планета не является плоской, а имеет шарообразную форму. Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений древнего мира.

Первый известный науке метод определения размеров Земли применил греческий учёный Эратосфен, живший в Египте. Его идея была достаточно проста. Итак, Эратосфен выбрал два города — Александрию и Сиену (ныне Асуан) — расположенных на одном земном меридиане.

Далее он обозначил длину дуги меридиана между двумя городами через l, а её угловое значение в градусах как п.

Тогда длина дуги в 1 о выбранного меридиана равна

С другой стороны, он знал, что длина окружности равна: L = 2πR.

Приравняв правые части последних двух уравнений, легко получить искомый радиус земного шара:

Теперь было необходимо определить длину дуги меридиана в градусной мере. Очевидно, что она равна разности географических широт Александрии и Сиены. Так вот, чтобы определить эту разность Эратосфен придумал хитрый способ. Он знал, что в полдень дня летнего Солнцестояния в Сиене Солнце находится в зените и освещает дно самых глубоких колодцев. А в Александрии Солнце до зенита не доходит. Поэтому шест, вбитый вертикально в землю должен отбрасывать тень. Измерив длину этой тени можно легко определить искомую длину дуги меридиана, которая у Эратосфена оказалась равной 7,2 о .

Ну а расстояние между Александрией и Сиеной ему было хорошо известно: оно составляло пять тысяч греческих стадий.

Подставив все данные в формулу для длины окружности меридиана, Эратосфен получил значение в 250 000 стадий.

Стадий — это весьма неоднозначная единица измерения расстояния. Но, как правило, за стадий принимали расстояние, которое проходит легковооружённый воин за промежуток времени от появления первого луча солнца при его восходе до того момента, когда весь солнечный диск окажется над горизонтом.

Однако если учесть, что расстояние между Александрией и Асуаном по прямой примерно равно 844 километрам, то можно полагать, что одна стадия примерно равна 169 метрам.

Тогда искомая длина всей окружности меридиана равна 42 250 километрам, что совсем не плохо для того времени.

Современная наука располагает более точными способами измерения расстояний на земной поверхности. Одним из них является метод триангуляций, основанный на явлении параллактического смещения.

Параллактическое смещение — это изменение направления на предмет при перемещении наблюдателя. С его помощью можно измерить расстояние на основе измерения длины одной из сторон (базиса) и двух прилегающих к ней углов в треугольнике.

Суть метода триангуляций состоит в следующем. По обе стороны дуги, длину которой нужно измерить, выбирается несколько точек на расстоянии не более 50 километров друг от друга, на которых устанавливаются геодезические вышки. При этом из каждой точки должны быть видны по крайней мере две другие точки. Далее тщательным образом измеряется длина базиса (с точностью до одного миллиметра). После этого с вершины вышки при помощи теодолита измеряются углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон по известным тригонометрическим формулам. Проводя затем измерение углов из пунктов, расстояние между которыми уже вычислено, можно узнать длину очередных двух сторон и так далее. Затем, по вычисленным сторонам, определяется искомая длина дуги.

В XVIII веке использование триангуляционных измерений в экваториальных широтах и вблизи северного полярного круга, показало, что длина дуги в 1 о меридиана не одинакова и увеличивается к полюсам. Из этого следовало, что наша планета не является идеальным шаром и её полярный радиус почти на 21 километр короче экваториального. Поэтому в геодезии и форму Земли считают геоидом, то есть телом с поверхностью, близкой к поверхности спокойного океана и продолженной под материками.

В настоящее время форму Земли принято характеризовать следующими физическими характеристиками:

· полярное сжатие — 0,0033528;

· экваториальный радиус — 6378,1 км;

· полярный радиус — 6356,8 км;

· средний радиус — 6371,0 км;

· и длина окружности экватора — 40 075,017 км.

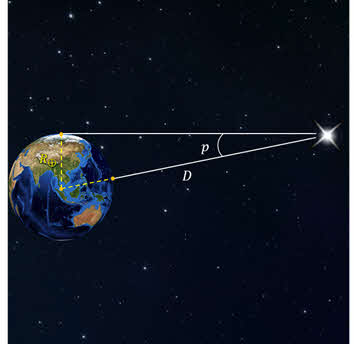
Долгое время загадкой для многих астрономов являлось истинное расстояние от Земли до Солнца. Измерить его смогли лишь во второй половине XVIII века, когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.

Горизонтальным параллаксом называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения.

Зная горизонтальный параллакс светила, можно, по известным тригонометрическим соотношениям, определить его расстояние от центра Земли:

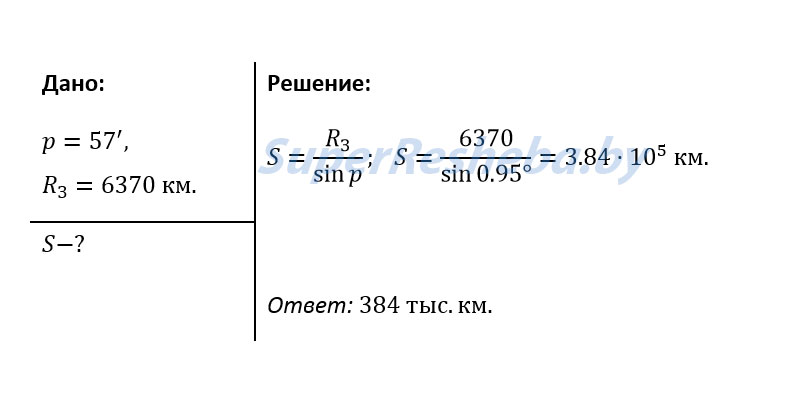
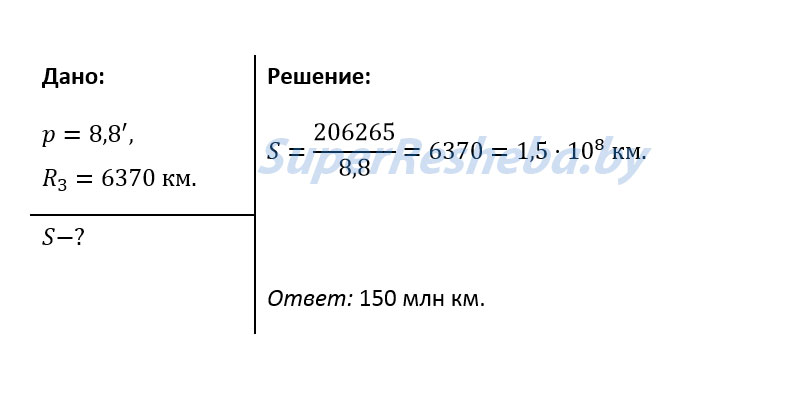
Очевидно, что чем дальше расположено светило, те меньше его горизонтальный параллакс. Например, наибольший параллакс, в среднем 57ʹ, имеет спутник Земли — Луна. У Солнца он значительно меньше и примерно составляет 8,794ʹʹ. Такому параллаксу соответствует среднее расстояние от Земли до Солнца, примерно равное 149,6 миллиона километров.

На одном из прошлых уроков мы говорили о том, что это расстояние в астрономии принимается за одну астрономическую единицу. С её помощью удобно измерять расстояния между телами в Солнечной системе.

Но вернёмся к нашей формуле. Итак, из геометрии вам должно быть известно, что при малых значениях угла его синус примерно равен самому углу, выраженному в радианах. Если учесть, что в одном радиане содержится 206 265ʹʹ, то легко можно получить формулу, удобную для вычислений:

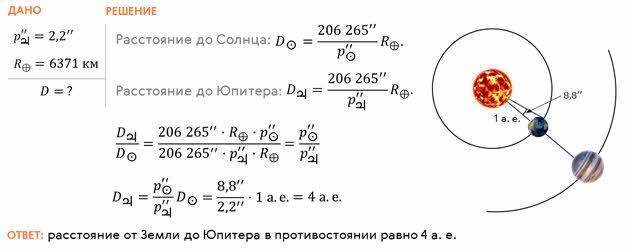
Для примера, давайте с вами определим расстояние от Земли до Юпитера в момент противостояния, если его горизонтальный параллакс был равен 2,2ʹʹ. Радиус Земли примем равным 6371 километру.

Эту же задачу можно было решить несколько иначе.

В настоящее время для более точного определения расстояний до тел в Солнечной системе применяется более точный метод измерений — радиолокационный. Измерив время, необходимое для того, чтобы радиолокационный импульс достиг небесного тела, отразился и вернулся на Землю, вычисляют расстояние до этого тела по формуле:

где с — это скорость света в вакууме.

С разработкой методов определения расстояний до тел в Солнечной системе учёным не составило большого труда придумать и способ определения их размеров. В частности, при наблюдениях небесного тела Солнечной системы с Земли можно измерить угол, под которым оно видно наблюдателю, то есть его угловой размер (или угловой диаметр), а, следовательно, и угловой радиус.

А зная угловой радиус и расстояние до светила, можно вычислить его линейный радиус:

.

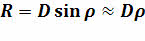
Только в этой формуле угловой радиус должен быть выражен в радианах.

Если в записанное уравнение подставить формулу для определения расстояний методом горизонтального параллакса и упростить её, используя тот факт, что значения углов ρ и р малы, то получим формулу, по которой можно определять линейные размеры небесных тел:

Но помните, пользоваться ей можно тогда, когда видны диски светил.

Для примера давайте решим с вами такую задачу. При наблюдении прохождения Меркурия по диску Солнца определили, что его угловой радиус равен 5,5’’, а горизонтальный параллакс — 14,4’’. Чему равен линейный радиус Меркурия?

Источник