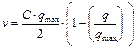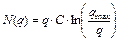- Определение тарифных расстояний
- Расчет расстояний для грузоперевозок
- Расчет коротких расстояний
- Расчет расстояний для междугородних маршрутов
- Калькулятор расстояний АвтоТрансИнфо
- Онлайн расчет расстояния на калькуляторе
- Калькулятор расстояний АвтоДиспетчер
- Онлайн расчет на калькуляторе АвтоДиспетчер
- Калькулятор расстояний Флагма
- Онлайн расчет на расстояния на калькуляторе Флагма
- Расчет расстояний портативным навигатором
- Моделирование транспортных сетей и расчет кратчайших расстояний
Определение тарифных расстояний
Тарифное расстояние — это расстояние между станциями отправления и назначения, за которое взимается провозная плата. Тарифное расстояние, согласно Прейскуранту №10‑01 / 8 /, определятся по Тарифному руководству №4, с учетом особенностей перевозимого груза, подвижного состава, географического расположения станций и участков железных дорог, характеризующихся особыми условиями функционирования.
Тарифным расстоянием считается (согласно Прейскуранту №10‑01, раздел 2, п.2.1):
- расстояние по кратчайшему направлению перевозки;
- действительно пройденное расстояние при перевозке негабаритных грузов и грузов на транспортерах;
- суммарное расстояние по РЖД при перевозках грузов с участием Калининградской железной дороги;
- расстояние перевозки с учетом обхода железнодорожных узлов для ряда опасных грузов и остальных грузов с учетом обхода малодеятельных участков и скоростных линий (список которых публикуется отдельно), а также с учетом особого порядка определения тарифных расстояний, указанного в Прейскуранте №10‑01, прил.1.
Тарифное руководство №4 предназначено для определения тарифных расстояний в границах железнодорожных администраций, входящих в Совет по железнодорожному транспорту государств — участников содружества, Латвийской Республики, Литовской Республики, Эстонской Республики, для перевозки грузов, пассажиров и
грузобагажа.
Это руководство состоит из 3-х книг:
Книга 1 Тарифные расстояния между станциями участков железных дорог;
Книга 2 ч.1. Алфавитный список железнодорожных станций с указанием выполняемых на них коммерческих операций;
ч.2. Алфавитный список пассажирских остановочных
пунктов;
Книга 3 Тарифные расстояния между транзитными пунктами.
Для исчисления расстояний следует:
1. В алфавитном списке станций (Тарифное руководство №4, кн.2, ч.1) найти станции отправления и назначения и определить на каком участке и между какими узлами расположены каждая из них.
Выписать указанные в графе 5 расстояния от станций отправления и назначения до узловых транзитных пунктов.
2. По схемам железных дорог РФ или «Схеме узловых и транзитных пунктов и тарифных расстояний по сети ж.д.» определить кратчайшее направление перевозки .
Рис.4.1. Схемы расположения станций:
а) в пределах одного участка б) на двух смежных участках
Возможны следующие случаи определения расстояний:
1. Станции отправления и назначения расположены в пределах одного участка дороги (рис. 4.1.,а). В этом случае тарифное расстояние LТ будет равно разности расстояний от станции назначения l2 и отправления l1до одного из узлов участка, на котором находятся эти станции
Расстояния l1 и l2 находятся по книге 2, часть 1 (Тарифное
руководство №4).
2. Станции отправления и назначения расположены надвух смежных участках (рис.4.1,б). Тогда расстояние LТ равно сумме расстояний от станции отправления l1 и станции назначения l2 до общей для них узловой станции.
3. Станции отправления и назначения расположены наразных участках, между которыми находится один или несколько транзитных участков. В этом случае искомое расстояние LТ находится суммированием расстояний от станции отправления до ближайшего по направлению перевозки узлового пункта l1, между узловыми или транзитными пунктами LК,находящимися на кратчайшем пути, и от последнего узловогопункта до станции назначения l3. Расстояния l1 и l3 определяются по книге 2, а LК — по книге 3 Тарифного руководства №4
Рис.4.2. Схема расположения станций
Если заранее не известны названия узловых пунктов, лежащих на кратчайшем пути между станциями отправления и назначения, то кратчайшее (тарифное) расстояние находится как минимальная величина из четырех возможных комбинаций (см. рис.4.2.)
Определение срока доставки
В соответствии со статьей 33 «Устава железнодорожного транспорта Российской Федерации» / 3 / перевозчики обязаны доставлять груз по назначению и в установленные сроки. Исчисление срока доставки груза начинается с 24 часов дня приема груза к перевозке.
Нормативные сроки доставки грузов исчисляются на железнодорожной станции отправления исходя из расстояния, по которому рассчитывается плата за перевозку и норм суточного пробега вагонов в километрах на весь путь следования в зависимости от расстояния перевозки, вида отправки и вида скорости (табл.П.4.5, П.4.6).
Скорость перевозки грузов выбирает и указывает в оригинале транспортной железнодорожной накладной грузоотправитель. Если допускается перевозка данных конкретных грузов только большой скоростью, грузоотправитель должен указать большую скорость
Расчет срока доставки производится по формуле

где tНКО – время на начально-конечные операции, (2сут.)/ /;
LT – тарифное расстояние, км;
VСУТ ‑ норма суточного пробега, км;

При расчете срока доставки неполные сутки считаются за полные.
4.3.Расчет тарифных плат за перевозку грузов
Расчет тарифных плат за перевозку грузов производится по правилам, приведенным в Прейскуранте 10–01; ч.1:
раздел 1. Общие положения;
раздел 2. Правила применения тарифов для определения платы за перевозку по РЖД грузов в прямом железнодорожном, прямом смешанном сообщении, в непрямом смешанном сообщении и экспортно-импортных грузов следующих через российские порты, а также за услуги инфраструктуры;
раздел 3. Правила применения тарифов при определении платы за перевозку по РЖД экспортных и импортных грузов через пограничные передаточные станции РФ (за исключением транзита) и за услуги инфраструктуры.
Источник
Расчет расстояний для грузоперевозок
При планировании грузоперевозки важным этапом является расчет расстояния, которое преодолеет груз. От этого расстояния будет зависеть стоимость транспортировки и скорость прибытия груза. В рамках этой статьи постараемся провести обзор некоторых сервисов в Интернете, с помощью которых можно более или менее точно оценить протяженность маршрута.
Расчет коротких расстояний
Для расчета длины маршрута внутри населенного пункта могут пригодится такие сервисы как Яндекс.Карты. Воспользовавшись инструментом «Линейка», можно проложить интересующий маршрут поверх карты, по видимым на схеме или спутниковой карте дороге.
Этот способ применим, когда вы хорошо знаете город. Из-за проекции Меркатора, применяемой для рисования карт, расчет больших расстояний имеет сильную погрешность, т.к. не учитывается кривизна Земли.
Расчет расстояний для междугородних маршрутов
Для расчета расстояний в масштабах страны существуют некоторые сервисы. Рассмотрим подробнее наиболее популярные для грузоперевозок на дальние дистанции.
Калькулятор расстояний АвтоТрансИнфо
Это калькулятор расстояний попросит ввести начальную и конечную точку маршрута. Кроме того, можно указать промежуточные точки, если планируется заехать туда, или эта дорога по каким-либо причинам предпочтительней.
В настройках поиска маршрута можно указать: Разрешить паромы, разрешить «зимники», маршрут в пределах страны, самый «короткий» маршрут, самый «быстрый» маршрут, показывать только крупные пункты и показывать карту.
Результатом расчета будет карта с маршрутом, приблизительное расстояние и время в пути, а также схема с промежуточными точками и временными метками нарастающим итогом.
Онлайн расчет расстояния на калькуляторе
Калькулятор расстояний АвтоДиспетчер
Этот калькулятор очень похож на первый. Он имеет меньше настроек (только промежуточные точки), однако может приблизительно посчитать количество затраченного топлива и его стоимость. Для этого надо внести средний расход и стоимость топлива.
Онлайн расчет на калькуляторе АвтоДиспетчер
Калькулятор расстояний Флагма
Этот сервис расчета расстояний может учитывать промежуточные точки. Имеет настройки по использованию в маршруте паромов и грунтовых дорог. Для расчета скорости предлагается выбор из легкового и грузового автомобилей.

Онлайн расчет на расстояния на калькуляторе Флагма
Расчет расстояний портативным навигатором
Одним из популярных инструментов для расчета расстояний по дорогам является портативный автомобильный спутниковый навигатор. 
Практически все системы, устанавливаемые на подобные приборы способны вычислять расстояния с некоторыми настройками. При этом на экране отобразится ориентировочное время в пути, приблизительное время прибытия и общая дистанция.
Источник
Моделирование транспортных сетей и расчет кратчайших расстояний
При планировании перевозок возникает необходимость в определении кратчайших расстояний между АТО, пунктами потребления и пунктами отправления грузов. Кратчайшие расстояния между пунктами являются основой для оплаты клиентами транспортных услуг, для учета расхода топлива, определения грузооборота АТО, расчета заработной платы водителей и т.д.
Определение расстояний перевозок осуществляется несколькими практическими способами.
1) Непосредственный замер расстояний по местности. Этот метод мало пригоден из-за значительных расстояний, на которые перевозятся грузы.
2) Обкатка маршрутов на автомобиле может производиться на основании показаний штатного спидометра или специального измерителя расстояний, который представляет собой дополнительное колесо с устройством для фиксации числа оборотов.
3) Замер по карте (плану) города или района с помощью курвиметра.
Всем этим способам присущ один серьезный недостаток: нет гарантии, что выбранный путь будет кратчайшим. Этот недостаток особенно сказывается при густоразветвленной дорожной сети современных городов, когда между удаленными точками имеется множество различных путей.
Для нахождения оптимального решения используются математические методы, при применении которых необходима в качестве исходных данных транспортная сеть, отражающая транспортные связи между различными точками.
Построение модели транспортной сети. Множество всех дорог города или района составляет дорожную сеть. Транспортная сеть — это совокупность дорог региона, пригодных для движения заданных транспортных средств.
Модель транспортной сети может быть представлена в виде графа.
Граф — это фигура, состоящая из точек (вершин) и соединяющих их отрезков (звеньев).
Вершины графа — это точки на сети, наиболее важные для определения расстояний или маршрутов движения.
Звенья графа — это отрезки транспортной сети, характеризующие наличие дорожной связи между соседними вершинами. Звенья графа характеризуются числами, которые могут иметь различный физический смысл. Чаще всего это расстояние, но может использоваться, например, и время движения.
Ориентированные по направлению звенья графа называются дугами.
Фактически всякое неориентированное звено графа включает в себя две равноценные, но противоположно направленные дуги. В зависимости от того, все или часть звеньев имеют направление, граф является ориентированным или смешанным. Граф, каждая вершина которого может быть соединена некоторой последовательностью звеньев с любой другой его вершиной, называется связанным графом. Иначе говоря, каждая вершина связанного графа должна иметь как минимум одну входящую и одну выходящую дугу. Граф, моделирующий транспортную сеть, обязательно должен быть связанным, чтобы всегда был путь из любой вершины в любую другую вершину.
Моделирование транспортной сети начинают с размещения вершин графа. За вершины графа принимают ГОП, ГПП, центры крупных жилых кварталов или небольших обособленных жилых пунктов и пересечения улиц. Каждой вершине присваивается порядковый номер или другое условное обозначение. После размещения вершин их связывают дугами или звеньями.
При построении модели транспортной сети особое внимание следует уделить максимально возможному уменьшению числа вершин. В противном случае транспортная сеть будет излишне сложна и определение кратчайших расстояний потребует длительного времени.
Одним из наиболее тривиальных методов определения минимального расстояния на графе является метод потенциалов.
Метод потенциалов для определения кратчайших расстояний заключается в следующем. Начальной вершине сети, за которую может быть принята любая из вершин, присваивают потенциал, равный нулю. Затем определяют потенциалы соседних с начальной точкой вершин сети. Значение потенциала равно расстоянию до вершины. Выбирают наименьший потенциал и присваивают его соответствующей вершине. Затем вычисляют потенциалы вер шин, соседних с выбранной, и снова выбирают наименьший потенциал и присваивают его соответствующей вершине и т.д.
Полное решение задачи включает в себя столько этапов, сколько вершин имеет транспортная сеть, поскольку на каждом этапе определяют потенциал или кратчайшее расстояние от начальной точки до одной из вершин сети.
Вопросы для повторения
1. Какими практическими способами определяется непо?
2. Что такое критерий оптимальности?
3. В чем особенность решения задач на транспорте методом линейного программирования?
4. Какие особенности характерны для задача линейного программирования?
5. В чем особенность решения задач на транспорте методом нелинейного программирования?
Формулировка и методы решения транспортной задачи
Оптимальное закрепление поставщиков однородного груза за потребителями, т.е. нахождение оптимальных грузопотоков, является классическим примером транспортной задачи. В этом случае потребителя не интересует, с какого конкретно склада ему будет доставлен, например, щебень. Но с точки зрения снижения транспортных издержек может наблюдаться существенная разница. Уменьшение расстояния перевозки грузов от поставщиков к потребителям в этом случае будет являться основным резервом снижения транспортных издержек.
В отдельных случаях транспортная задача может решаться не только для определения минимума пробега, который будет выполнен для доставки груза, но и для определения наиболее короткого времени, требуемого для выполнения перевозок, или их минимальной стоимости. В этом случае вместо матрицы расстояний между поставщиками и потребителями необходимо использовать матрицы времени движения или стоимости перевозок. Так как в подавляющем большинстве случаев перевозчик заинтересован в минимизации пробега, то в дальнейшем будет рассматриваться транспортная задача только на определение минимума расстояния (грузооборота).
Суть транспортной задачи линейного программирования состоит в следующем:
В пунктах отправления А1, А2, . Аn, имеется однородный груз в количестве а1, а2, . аn. Этот груз необходимо доставить в пункты потребления В1, В2, . Вm в количестве b1, b2 . bm. Известны кратчайшие расстояния сij, между всеми пунктами отправления и получения груза. Необходимо построить план перевозок таким образом, чтобы была удовлетворена потребность в грузе всех пунктов потребления, был бы вывезен весь груз из пунктов производства и при этом был бы обеспечен минимум транспортной работы в тонно-километрах.
Имеется m пунктов отправления (или пунктов производства) Аi …, Аm, в которых сосредоточены запасы однородных продуктов в количестве a1, . аm единиц. Имеется n пунктов назначения (или пунктов потребления) В1, . Вm, потребность которых в указанных продуктах составляет b1, . bn единиц. Известны также транспортные расходы Сij, связанные с перевозкой единицы продукта из пункта Ai в пункт Вj, i 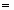
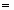
 | (2.11) |
Требуется составить такой план перевозок (откуда, куда и сколько единиц продукта везти), чтобы удовлетворить спрос всех пунктов потребления за счет реализации всего продукта, произведенного всеми пунктами производства, при минимальной общей стоимости всех перевозок. Приведенная формулировка транспортной задачи называется замкнутой транспортной моделью. Формализуем эту задачу.
Пусть хij — количество единиц продукта, поставляемого из пункта Аi в пункт Вj. Подлежащие минимизации суммарные затраты на перевозку продуктов из всех пунктов производства во все пункты потребления выражаются формулой:
 | (2.12) |
Суммарное количество продукта, направляемого из каждого пункта отправления во все пункты назначения, должно быть равно запасу продукта в данном пункте. Формально это означает, что
 , i =1, …, m , i =1, …, m | (2.13) |
Суммарное количество груза, доставляемого в каждый пункт назначения из всех пунктов отправления, должно быть равно потребности. Это условие полного удовлетворения спроса:
 , j =1, …, n , j =1, …, n | (2.14) |
Объемы перевозок — неотрицательные числа, так как перевозки из пунктов потребления в пункты производства исключены:
xij ≥0, i 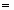 1, . m; j =1, . n 1, . m; j =1, . n | (2.15) |
Транспортная задача сводится, таким образом, к минимизации суммарных затрат при выполнении условий полного удовлетворения спроса и равенства вывозимого количества продукта запасам его в пунктах отправления.
Всякое неотрицательное решение системы линейных уравнений

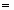

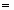
определяемое матрицей X=(xij)(i 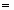
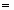



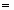
принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные записываются в виде таблицы 2.1.
Очевидно, общее наличие груза у поставщиков равно 
 | (2.16) |
то модель такой транспортной задачи называется закрытой.
Транспортная задача, в которой суммарные запасы и потребности не совпадают, т. е. не выполняется условие 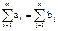
а) суммарные запасы превышают суммарные потребности 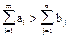
б) суммарные потребности превышают суммарные запасы 
Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.
Открытая модель решается приведением к закрытой модели.
В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель Bn+1, потребности которого bn+1 = 

Стоимость перевозки единицы груза как фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.
После преобразований задача принимает вид закрытой модели и решается обычном способом. При равных стоимостях перевозки единицы груза от поставщиков к фиктивному потребителю затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. То же самое получаем и в отношении фиктивного поставщика.
Прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверить, к какой модели она принадлежит, и только после этого составить таблицу для ее решения (таблица 2.1).
Определение оптимального и опорного плана транспортной задачи
Определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана.
Число переменных Xij в транспортной задаче с m пунктами отправления и n пунктами назначения равно nm, а число уравнений равно n+m. Так как мы предполагаем, что выполняется условие (1), то число линейно независимых уравнений равно n+m-1.
Если в опорном плане число отличных от нуля компонентов равно в точности n+m-1, то план является не выраженным, а если меньше — то выраженным.
Для определения опорного плана существует несколько методов. Три из них — метод северно-западного угла, метод минимального элемента и метод аппроксимации Фогеля — рассмотрены ниже.
При составлении первоначального опорного плана методом северо-западного угла стоимость перевозки единицы не учитывается, поэтому построенный план далек от оптимального, получение которого связано с большим объемом вычислительных работ.
Для определения оптимального плана транспортной задачи можно использовать изложенные ниже методы. Ввиду исключительной практической важности этой задачи и специфики ее ограничений для определения оптимального плана транспортной задачи разработаны специальные методы. Один из них — Венгерский метод — рассматриваются ниже.
Методы определения первоначального опорного плана
Метод северо-западного угла
Построение допустимого первоначального плана методом северо-западного угла начинается с заполнения левой верхней клетки матрицы и заканчивается в правой нижней клетке матрицы. В каждую клетку заносят максимально возможную поставку, учитывая при этом возможности поставщика и спрос потребителя.
Груз, имеющийся у первого поставщика, распределяется так, чтобы сначала по возможности полностью удовлетворить потребности первого потребителя, потом второго и т.д. Затем переходят к распределению груза, имеющегося у второго поставщика, и так до полного распределения груза у всех поставщиков. Если спрос какого-либо потребителя превышает наличие груза у поставщика, то недостающий спрос удовлетворяют за счет следующего поставщика.
Способ построения первоначального допустимого плана методом северо-западного угла очень прост, но, как правило, полученный план далек от оптимального. Это объясняется тем, что составление плана производится механически, без учета расстояний между пунктами или стоимости перевозок.
Метод минимального элемента
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел ai и bj. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Метод аппроксимации Фогеля
При определении опорного плана транспортной задачи методом аппроксимации Фогеля находят разность по всем столбцам и по всем строкам между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальная стоимость.
Если минимальная стоимость одинакова для нескольких клеток столбца (строки), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разности между двумя минимальными стоимостями, находящимися в данном столбце (строке).
Методы определения оптимального плана
Идея метода была высказана венгерским математиком Эгервари и состоит в следующем. Строится начальный план перевозок, не удовлетворяющий в общем случае всем условиям задачи (из некоторых пунктов производства не весь продукт вывозится, потребность части пунктов потребления не полностью удовлетворена). Далее осуществляется переход к новому плану, более близкому к оптимальному. Последовательное применение этого приема за конечное число итераций приводит к решению задачи.
Алгоритм венгерского метода состоит из подготовительного этапа и из конечного числа итераций. На подготовительном этапе строится матрица X0 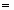
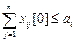 , i =1, …, m; , i =1, …, m;  , j =1, …, m. , j =1, …, m. | (2.17) |
Если эти условия являются равенствами, то матрица Хo — решение транспортной задачи. Если среди условий имеются неравенства, то осуществляется переход к первой итерации. На k-й итерации строится матрица Хk 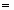
 . . | (2.18) |
В результате первой итерации строится матрица Хl, состоящая из неотрицательных элементов. При этом Δl 
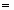

Венгерский метод наиболее эффективен при решении транспортных задач с целочисленными объемами производства и потребления. В этом случае число итераций не превышает величины Δ0/2 (Δ0 — суммарная невязка подготовительного этапа).
Достоинством венгерского метода является возможность оценивать близость результата каждой из итераций к оптимальному плану перевозок. Это позволяет контролировать процесс вычислений и прекратить его при достижении определенных точностных показателей. Данное свойство существенно для задач большой размерности.
Примеры решения задач
1) Построить модели Гриншильдса, Гринберга и обобщенную для (n=0,2).
При условие интесивности движения Nmax = 1200 авт/час, qmax = 20 авт/км. C = 140 км/ч
А) Модель Гринберга:
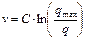
Учитывая уравнение состояния:


Б) Модель Гриншильдса

Учитывая уравнение состояния:

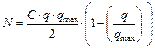
В)Обобщенная модель n =0,2

2) Посчитать мгновенную и среднюю скорость потоков для условий (qmax= 20 авт/км, С = 150 км/ч):
Для плотности потока q = 10 авт/км
Для плотности потока q = 15 авт/км
Для плотности потока q = 18 авт/км
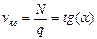
3) Посчитать вероятность того что из 3-х погрузочно разрузоных устройств 2 будут заняты (все устройства свободны), если время обслуживания – 20мин, а промежуток через который поступает требование 30 минут
| α= λtоб/=λ/v. | (1.59) |
Вероятность того, что обслуживанием поступающих требований заняты к устройств, равна
| Pk=(ak/k!)/ Σ(ak/k!), | (1.60) |
где k изменяется от 0 до n — числа обслуживающих устройств.
Вероятность того, что все обслуживающие устройства свободны:
| P0=1/ Σ(ak/k!). | (1.61) |
Вероятность того, что все обслуживающие устройства заняты:
| Pn=P0/(ak/k!). | (1.62) |
2 будут свободны:
Все будут свободны
Тест для самопроверки
- Процесс моделирования это:
- Процесс создания модели объекта-оригинала, его исследования и распространения результата исследования на объект-оригинал
- Процесс создания программных модулей в целом отображающих свойства модели
- Процесс создания математического описания существующих процессов и физических свойств объекта-оригинала
- Модель это:
- некоторая система, воспроизводящая свойства объект-оригинала, которые полагаются существенными и не содержащая свойств объект-оригинала, которые считаются несущественными.
- некоторая система, описывающая объект-оригинал как совокупность его физических свойств.
- некоторая система, воспроизводящая все свойства объект-оригинала.
- Выберите существующие виды моделей, которые используются при моделировании задача ТП:
- физические, воспроизводящие изучаемый процесс с сохранением его физической природы
- химические, воспроизводящие изучаемый процесс с сохранением его химической природы
- математические, описывающие процессы в ОО в математических терминах
- Какие из перечисленных ниже моделей не имеют отношение к математическим моделям:
- Аналитические
- Изоморфные
- Компьютерные
- Физические
- Что такое интенсивность движения:
- это количество транспортных средств, проходящих через сечение дороги за единицу времени – год, месяц, час, минута, секунда
- величина, характеризующаяся соотношением в нем транспортных средств различного рода
- это количеством транспортных средств, приходящихся на 1 км протяженности полосы дороги
- Что такое плотность потока:
- это количество транспортных средств, проходящих через сечение дороги за единицу времени – год, месяц, час, минута, секунда
- величина, характеризующаяся соотношением в нем транспортных средств различного рода
- это количеством транспортных средств, приходящихся на 1 км протяженности полосы дороги
- Состав ТП:
- это количество транспортных средств, проходящих через сечение дороги за единицу времени – год, месяц, час, минута, секунда
- величина, характеризующаяся соотношением в нем транспортных средств различного рода
- это количеством транспортных средств, приходящихся на 1 км протяженности полосы дороги
- Особенности транспортного потока как объекта исследования, исключите лишнее:
- Нестационарность
- Стохастичность
- Неполная управляемость
- Множественность критериев управления
- Возможность распространения результатов измерения всех основных параметров ТП в текущем срезе времени, на любой момент времени движения ТП
- невозможность замера практически всех характеристик качества управления
- принципиальная невозможность проведения масштабных натурных экспериментов в сфере управления дорожным движением
- Какие из представленных моделей относятся к детерминированным:
- Микроскопические
- Детерминированные
- Макроскопические
- Какие из представленных моделей относятся к стохастическим:
- Микроскопические
- Детерминированные
- макроскопические
- Детерминированные модели:
- модели, в основу которых заложена функциональная зависимость между отдельными показателями ТП
- модели, рассматривающие ТП как вероятностный, случайный процесс
- Стохастические модели:
- модели, в основу которых заложена функциональная зависимость между отдельными показателями ТП
- модели, рассматривающие ТП как вероятностный, случайный процесс
- Математическая модель это
- комплекс основных соотношений, описывающих поведение объекта, выраженный с использованием математических соотношений;
- комплекс основных соотношений, описывающих поведение объекта;
- уменьшенная копия объекта-оригинала;
- Аналитический способ исследования применим для
- физических моделей;
- математических моделей;
- имитационных моделей.
- Имитационное моделирование имеет в своей основе
- некоторое аналитическое выражение;
- некоторый алгоритм;
- программу на языке высокого уровня.
- Какая характеристика имеет размерность авт/км?
- задержки;
- плотность;
- интенсивность.
- Какая особенность характеризует изменчивость ТП на различных временных отрезках?
- нестационарность;
- стохастичность;
- интенсивность.
- Стохастичность ТП это
- свойство, при котором все управляющие воздействия сводятся лишь к «советованию»;
- вероятностный характер поведения ТП;
- свойство не полной управляемости ТП.
- Детерминированные модели ТП характеризуются
- вероятностными соотношениями;
- нестационарностью ТП;
- аналитическими зависимостями между основными характеристиками ТП.
- Детерминированные модели ТП применяют
- при исследовании ТП высокой плотности;
- при исследовании ТП низкой плотности;
- для исследования движения одного ТС в ТП.
- В основе стохастическх моделей лежит идея
- что характеристики ТП являются случайными величинами;
- что характеристики ТП являются неслучайными величинами;
- что главная характеристика ТП это скорость.
- Какие модели применяются для анализа поведения автомобиля в ТП
- макроскопические;
- детерминированные;
- микроскопические.
- Модели, которые применяются для анализа поведения ТП?
- макроскопические;
- детерминированные;
- микроскопические.
- Модель Гриншильдса
a) линейная зависимость между скоростью и плотностью;
b) нелинейная зависимость между скоростью и плотностью;
c) произведение плотности на скорость;
- Уравнение состояния ТП это
a) произведение плотности ТП на скорость ТП;
b) отношение плотности ТП к скорости ТП;
c) первая производная координаты по времени;
- Количество автомобилей, въезжающих на участок дороги равно количеству автомобилей покидающих участок дороги есть суть уравнения
b) неразрывности ТП;
- Модель Гринберга получается из обобщенной модели ТП при
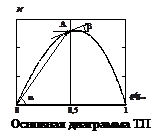
- Основная диаграмма ТП это
a) зависимость плотности от скорости;
b) интенсивности от задержек ТП;
c) интенсивности от плотности;
- С помощью основной диаграммы ТП можно определить
a) мгновенную скорость ТП;
- На рисунке, представленном ниже tg(a) это
a) средняя скорость ТП;
b) скорость распространения кинематической волны в ТП;
c) скорость волны изменения интенсивности ТП;
- При каком значении плотности ТП значение скорости распространения кинематической волны равно нулю?
- Ударная волна в ТП это явление когда
a) скорость ТП максимальна;
b) автомобили вынуждены многократно трогаться и останавливаться;
c) интенсивность максимальна;
- Модель, позволяющая учитывать реакцию водителя
b) Следования за лидером;
- Какими элементами характеризуется система массового обслуживания:
- Требование
- Очереди требований
- Входящий поток
- Интенсивность поступления требований
- Отсутствие последействия
- Выходящий поток
- Внутренний поток
- Очередь поступлений
- Обслуживающие устройства
- Обслуживающая система
- Требование:
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Очереди требований:
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Входящий поток
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Интенсивность поступления требований
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Отсутствие последействия
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Ординарность потока требований
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Выходящий поток
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований уже поступило в систему, т. е. не зависит от числа уже обслуженных требований
- означает практическую невозможность появления двух и более требований в один и тот же момент времени
- средства, которые осуществляют обслуживание
- совокупность обслуживающих устройств
- Обслуживающие устройства
- Это запрос на удовлетворение некоторой потребности в выполнении работ
- Это число требований, ожидающих обслуживания
- Это совокупность требований, поступающих с определенной закономерностью
- Это среднее число требований, поступающих в систему за единицу времен
- состоит в том, что вероятность поступления за отрезок времени t определенного числа требований не зависит от того, сколько требований
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Источник