Способы определения расстояние до галактики

Некоторые методы определения расстояний до галактик мы уже упоминали в предыдущих лекциях. Это метод диаметров , сыгравший большую роль в установлении Хабблом закона разбегания галактик, и метод ярчайших звёзд — самых ярких красных гигантов для близких эллиптических галактик и голубых и красных сверхгигантов для спиральных галактик. Но самым важным является метод, основанный на использовании зависимости период-светимость классических цефеид, который используется для определения расстояний до близких спиральных и неправильных галактик и служит основой для определения расстояний в ближайшей вселенной, так как именно с помощью наблюдения цефеид калибруется зависимость лучевая скорость-расстояние (закон Хаббла). Цефеиды в настоящее время остаются наиболее точными индикаторами расстояний (ошибка метода 10-20%) на промежутке до &#8776 10 Мпк (для сравнения — расстояние до Туманности Андромеды М31 приблизительно равно 700 кпк).

Примерно в тех же пределах (но с ошибкой до 50%) индикатором расстояния для спиральных и неправильных галактик, то есть галактик с большим количеством газа, могут служить облака ионизованного водорода . Дело в том, что диаметр крупнейшей области HII в галактике зависит от абсолютной звёздной величины этой галактики. Для определения расстояний до ближайших эллиптических галактик используются светимости переменных звёзд типа RR Лиры . Напомним также об использовании функции интегральной светимости шаровых скоплений для определения расстояний до галактик, о котором говорилось в лекции о шаровых скоплениях. Доступные методу предельные расстояния порядка 50 Мпк, при ошибке 25-50%. Сверхновые звёзды тоже используют для оценки расстояний, поскольку в максимуме блеска сверхновые типа Ia, например, имеют практически одинаковые абсолютные звёздные величины. В наземные телескопы их можно запечатлеть на расстоянии в половину размера Вселенной, а космический телескоп — на еще большем расстоянии. Типичная ошибка метода в определении расстояний до галактик 25-50%. Именно данные о сверхновых типа Ia, вспыхнувших в очень далеких галактиках, свидетельствуют, что примерно 5 млрд. лет назад замедление расширения Вселенной сменилось его ускорением.

К сожалению, сверхновые вспыхивают в галактиках редко и непрогнозируемым образом, поэтому для далеких галактик разработаны другие подходы. В частности, весьма перспективными представляются два метода, которые требуют наблюдения лучевых скоростей звёзд и межзвёздной материи внутри галактик. Первый, известный как метод Талли-Фишера , основан на использовании найденной ими 1977 году эмпирической зависимости между светимостями галактик позднего типа и ширинами в них линий 21 см (т.е. скоростями вращения галактик). Современные измерения приводят к соотношению: L &#8733 V_max 3.4 . Метод удобен для проведения массовых статистических исследований в далеких скоплениях галактик. Для галактик ранних типов расстояния можно находить на основе обнаруженной Фабер и Джексоном в 1976 году корреляции между светимостью нормальных эллиптических галактик и дисперсией скоростей их звёзд — это степенной закон L &#8733 &#963_V 4 . Наибольшую пользу метод может принести, если использовать его для измерений относительных расстояний между галактиками. Эти методы точнее, чем метод диаметров, но ошибки и в них могут достигать 50%. Оба метода основаны, как видим, на вполне ожидаемой из теоремы вириала зависимости: чем тяжелее галактика, тем выше скорости движения в ней звёзд и облаков газа. Однако существование обеих эмпирических зависимостей заставляет предполагать, что соотношения видимой и темной материи в галактиках соответствующих типов одинаково, что еще не нашло теоретического обоснования.

Перейдем теперь к определению расстояний до наиболее удаленных объектов, к которым неприменимы отмеченные выше методы. Введем так называемое красное смещение :

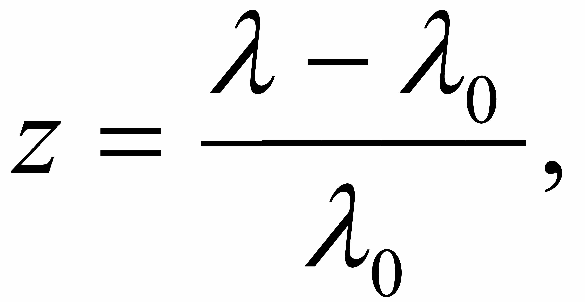при этом имеется приближенная формула для вычисления лучевой скорости: v_r &#8776 zc, где с — скорость света. Эдвин Хаббл установил, что приближенно для не очень близких галактик выполняется соотношение v_r = Hr, величину H называют постоянной Хаббла. Сидней ван ден Берг, проанализировав имеющиеся определения постоянной Хаббла, дал среднее из определений, выполненных ранее 1996 года: H = 72 км/с/Мпк. В 1999 году Тауэр, Фергюсон и Шэнкс, определив с помощью цефеид расстояния до галактик скопления в Деве, привели величину H = 67 7 км/с/Мпк. В настоящее время она полагается равной &#8776 70 км/с/Мпк. К сожалению, пекулярные скорости близких галактик, до которых расстояния определяются надежно, слишком велики по сравнению с хаббловской скоростью, а расстояния до далеких галактик очень ненадежны. Поэтому постоянная Хаббла до сих пор известна с ошибкой порядка 10 км/c/Мпк. Однако это единственный метод определения расстояния до далеких галактик, квазаров и скоплений галактик. По результатам космического эксперимента WMAP H₀ = 71 км /с/ Мпк с ошибкой &#8776 5%.

Более точная формула связи z и v_r , в отличие от приведенной выше верной для малых z, имеет вид:

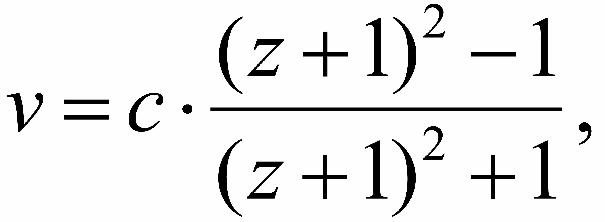Именно этой формулой пользуются в большинстве случаев для определения лучевой скорости, так как наблюдаемая величина z для самых далеких наблюдаемых внегалактических объектов достигает 3.5.

В последнее время для оценки расстояний до очень далеких галактик получает все большее распространение метод гравитационного линзирования — физическое явление, связанное с отклонением лучей света в поле тяжести. В результате гравитационного линзирования два луча света от объекта S, прошедшие по разные стороны от тела L, пересекаются в точке O, где располагается наблюдатель (см. рис. 19-2). Он увидит два изображения I₁ и I₂ одного и того же объекта S. Угловое расстояние между двумя изображениями примерно равно угловому размеру так называемого конуса Эйнштейна — воображаемого круга на небе с центром, совпадающим с центром линзы, размер которого пропорционален квадратному корню из массы линзы и обратно пропорционален квадратному корню из расстояния до нее от Земли. Так как оптические пути, формирующие два изображения, различны, то свет идет по ним разное время. И если в объекте произойдет вспышка, то она достигнет наблюдателя вначале по кратчайшему пути, лишь затем по длинному, т.е. повторится во втором изображении (в угловой мере более близком к телу-линзе). Измерив разность моментов прихода сигнала, можно определить и разность оптических путей, что в совокупности с известным угловым расстоянием между изображениями позволяет узнать расстояние до объекта и тела-линзы. В качестве тела-линзы могут выступать различные точечные объекты, например отдельные звёзды, черные дыры или далекие галактики.

В целом модули расстояния до отдельных галактик определяются с ошибками около 1 m .

Источник

Способы определения расстояние до галактики

Расстояние от наблюдателя до галактики как физическая характеристика не входит ни в один процесс, происходящий с галактикой. Необходимость в информации о расстоянии до галактики возникает при: отождествлении малоизученных событий, например, гамма-всплесков; изучении Вселенной как целого, изучении эволюции самих галактик, определении массы галактик и их размеров и т. п.

Все более-менее моделенезависимые способы определения расстояния до галактики можно разделить на два типа: измерение по объекту внутри галактики, расстояние до которого на пренебрежимо малую величину отличается от расстояния до самой галактики, и по красному смещению.

Первый способ — фотометрический способ, с использованием так называемых стандартных свеч, светимость которых считается известной. Тогда расстояние можно вычислить по следующей формуле:

где m — видимая звёздная величина, М — абсолютная звёздная величина, а R — расстояние, измеряемое в парсеках. На современном этапе в качестве таких стандартных свеч используют [10] :

· Цефеиды, зная период пульсаций которых, можно узнать их светимость. Первый объект, по которому измерили расстояние до других галактик.

· Сверхновые типа Ia. Именно с помощью них в 90-х годах XX века открыли ускоренное расширение Вселенной.

Второй способ основан на эмпирическом законе Хаббла и более зависим от выбранной модели, чем предыдущий.

где H₀ — постоянная Хаббла. Если же взять ныне распространённую ΛCDM-модель (с той же постоянной Хаббла), то сколько-нибудь существенное расхождение будет на z

10, что позволяет его причислить к относительно моделенезависимым.

Существует также ряд сильно моделезависимых способов [10] :

· по эффекту Сюняева — Зельдовича,

· по шаровым скоплениям,

· по зависимости Талли — Фишера,

· по зависимости Фабер — Джексона.

Галактики не имеют чётких границ. Нельзя точно сказать, где кончается галактика и начинается межгалактическое пространство. К примеру, если в оптическом диапазоне галактика имеет один размер, то определяемый по радионаблюдениям межзвёздного газа радиус галактики может оказаться в десятки раз больше. От размера зависит и измеряемая масса галактики. Обычно под размером галактики понимают фотометрический размер изофоты 25-й звёздной величины с квадратнойугловой секунды в фильтре B. Стандартное обозначение такого размера — D₂₅ [13] .

Масса дисковых галактик оценивается по кривой вращения в рамках некой модели. Выбор оптимальной модели галактики опирается как на форму кривой вращения, так и на общие представления о структуре галактики. Для грубых оценок массы эллиптических галактик необходимо знать дисперсию скоростей звёзд в зависимости от расстояния от центра и радиальное распределение плотности [14] .

Масса холодного газа в галактике определяется по интенсивности линии H I. Если регистрируемая плотность потока излучения от галактики или какой-либо её части равны F_ν, то соответствующая масса равна:

где D — расстояние в мегапарсеках, поток выражен в янских.

Оценка массы молекулярного газа весьма сложна, так как спектр самой распространённой молекулы H₂ не имеет линий, возбуждаемых в холодном газе. Поэтому исходными данными являются интенсивности спектральных линий молекулы CO (I_CO). Коэффициент пропорциональности между интенсивностью излучения CO и его массой зависит от металличности газа. Но самая большая неопределённость связана с малопрозрачностью облака, из-за неё основная доля света, излучаемая внутренними областями, поглощается самим же облаком, таким образом, до наблюдателя доходит свет только от поверхности облаков [15] .

Источник

Способы определения расстояние до галактики

Астрономический Институт Санкт-Петербургского Университета
Санкт-Петербург, 1997

Содержание.

Введение.

Построение точной шкалы расстояний во Вселенной является одной из фундаментальных проблем современной науки. В настоящее время в астрономии нет единого универсального способа определения расстояний до небесных тел. По мере перехода от близких объектов к более далеким один метод определения расстояний заменяется другим, причем каждый предыдущий обычно служит основой для последующего. Следует отметить, что прямые методы оценки расстояний, такие как измерение тригонометрических параллаксов, применимы всего лишь до расстояний не превышающих 100 пк. Расстояния до более далеких звезд, галактик, скоплений галактик приходится определять косвенными методами с использованием тех или иных космических индикаторов, характеристики которых нам известны. Ошибки при построении шкалы космических расстояний велики и чаще всего вызваны ошибками в отождествлении космических эталонов и неточностью их калибровки. И лишь в последние годы, благодаря прогрессу в наблюдательной астрофизике,удалось измерить расстояния до некоторых галактик с ошибкой не превышающей 20 %.

Детальные обзоры основных методов определения расстояний приводятся во многих работах (например, [1,2]).

Выбор того или иного метода зависит от многих факторов. Основными из них являются:

наблюдательные возможности (разрешается ли данная галактика на звезды, шаровые скопления или другие объекты);
морфологический тип галактики;
приемлемая точность определения расстояния и трудоемкость метода.

Продемонстрируем сравнение точности различных методов на примере оценки расстояния до скопления галактик в Деве — одного из ключевых вопросов современной астрофизики:

Совокупные ошибки в оценке расстояния до скопления в Деве

Тип неопределенностей

(m-M)
(зв.вел.)

TRGB
неопределенность фотометрического нуль-пункта HST	+/-0.03
ошибки моделей Функции Светимости красных гигантов	+/-0.06
ошибки в оценке поглощения света в направлении Девы	+/-0.02
внутренее рассеяние калибровки M_I (TRGB)	+/-0.10
неопределенность шкалы расстояний шаровых скоплений	+/-0.10
геометрическая глубина ядра скопления в Деве (+/-1 Мпк)	+/-0.13
Полная ошибка метода TRGB (для одной галактики)	+/-0.20

Цефеиды
переход в PL от БМО к спиральным галактикам Девы	+/-0.17
в оценке металличности цефеид	+/-0.05
в оценке расстояния до БМО	+/-0.10
в оценке отношения поглощения в направлении БМО и Девы	+/-0.02
геометрическая глубина спиральных галактик в Деве (+/-3 Мпк)	+/-0.35
Полная ошибка метода Цефеид (для одной галактики)	+/-0.41

Планетарные туманности
в построении наблюдаемых ФСПТ	+/-0.10
фотометрический нуль-пункт и калибровка фильтров	+/-0.06
в оценке отношения поглощения в направлении M31 и Девы	+/-0.02
в оценке расстояния до M31	+/-0.10
в определении опорной модели ФСПТ	+/-0.05
геометрическая глубина ядра скопления в Деве (+/-1 Мпк)	+/-0.13
Полная ошибка метода ФСПТ (для одной галактики)	+/-0.21

Краткий обзор основных методов определения расстояний до галактик.

1. Цефеиды.

Цефеиды на данное время остаются наиболее точными индикаторами расстояний на промежутке до 10 Мпк. Яркости цефеид заключены в пределах -2 m >M_v> -6 m и, вследствие переменности их блеска, они легко выявляются и классифицируются.

Классические цефеиды (I-го типа населения) — это молодые объекты, принадлежащие дисковой составляющей: они обнаруживаются в галактиках, в которых до недавнего времени происходило звездообразование, т.е. в S и Irr-галактиках. Периоды цефеид от нескольких дней до несколько сот дней.

Для получения расстояния по цефеидам требуются достаточно большие и точные ряды наблюдений. Но даже, если известен абсолютно точно период одной из цефеид в галактике, то ошибка в определяемом расстоянии составит около 30%. Причиной этого является разброс значений в зависимости период-светимость-цвет(PLC) — ширина полосы разброса, например, в цвете B — 1.2 m ; в V — 0.9 m ; а в B-V

0.4 m [3]. Для повышения точности требуется искать как можно больше цефеид в наблюдаемой галактике. В итоге ошибку можно свести к 10%. Кроме того, необходимо учитывать ошибку калибровки нуль-пункта соотношений PL и PC, которые определяются по цефеидам БМО и ММО, а также ошибки фотометрии.

В настоящий момент основные факторы, влияющие на неопределенность оценки расстояния до галактик по цефеидам, следующие:

Недостаточное число наблюдаемых цефеид;
Неточность в определении расстояния до БМО и ММО(+/-0.13 m ), цефеиды которых используют для калибровки соотношения PLC;
Неточность в оценке яркости цефеиды, вследствие отсутствия возможности точно учесть неравномерность поглощения света в галактике.

Большая трудоемкость и необходимость длительных рядов наблюдений привели к появлению вторичных индикаторов расстояний, которые калибруются, в основном, по цефеидам.

2. Сверхгиганты.

Для близких галактик,разрешимых на звезды (до 25 Мпк), в качестве «стандартной свечи» бывает целесообразно использовать ярчайшие звезды (голубые и красные сверхгиганты — BSG и RSG). Такие звезды представляют интерес еще и как предельные по массе и светимости образцы звезд.

Голубые сверхгиганты можно использовать для проверки Эддингтоновского предела светимости, поскольку ярчайшие из них находятся у этого предела, когда в звезде в равновесии световое давление и сила гравитации. У ярчайших BSG Mb= -10 m +/-0.15 m . Поэтому они различимы при современном уровне наблюдений до m-M=34 m (т.е. до 60 Мпк).

Физические причины существования предела светимости у RSG не до конца ясны, хотя наличие этого предела установлено эмпирически. Красные сверхгиганты также используют для проверки теории эволюции массивных звезд. Абсолютные болометрические звездные величины RSG порядка -9.5 m .

Важным событием в деле оценки расстояния до галактик с помощью ярчайших звезд стало использование зависимости между абсолютной звездной величиной ярчайших сверхгигантов и светимостью их родительской галактики, которая обсуждалась еще в работах Хаббла. Вид этой зависимости различен для BSG и RSG.

При использовании ярчайших звезд,как и при любом другом методе, основанном на небольшом числе экстремальных объектов в галактиках необходимо учитывать эффекты селекции.

3. Красные гиганты.

Sandage в 1971 году нашел [4], что ярчайшие красные гиганты имеют сходную абсолютную звездную величину M_v = -3.0 m +/-0.2 m и что их можно использовать для оценок расстояний. В наше время полагают, что эти красные звезды представляют либо крайнюю точку первого подъема ветви красных гигантов (RGB) звезд малых масс, либо более яркую асимптотическую ветвь гигантов (AGB).

Точность оценок расстояний (+/-0.2 m ) почти сравнима с первичными индикаторами расстояний: с цефеидами или звездами типа RR Лиры. Метод в то же время имеет ряд достоинств в сравнении с цефеидами и звездами типа RR Лиры:

Наблюдения показали, что I _TRGB в интервале ошибок +/-0.1 m не чувствительна к металличности [Fe/H] m , что на 4 m ярче, чем у звезд типа RR Лиры;
По сравнению с цефеидами, красные гиганты могут располагаться вдалеке от областей звездообразования,что уменьшает влияние поглощения на их звездную величину.

При современном уровне наземных телескопов метод может успешно применяться к галактикам, находящимся на расстояниях до (m-M)=28 m (

4 Мпк — порядка расстояния до группы M81) [5].

4. Метод флюктуаций поверхностной яркости.

Разрешимые на звезды галактики дают возможность изучать в них историю звездообразования, выделять отдельные типы звезд (сверхгиганты, цефеиды) и определять по ним расстояния до галактик. Однако большинство галактик не разрешается на звезды (в силу недостаточного углового разрешения), хотя приемники излучения способны зарегистрировать достаточное число фотонов от ярчайших звезд. Поэтому закономерным развитием метода ярчайших звезд стал метод флюктуаций поверхностной яркости, который можно использовать для эллиптических галактик или для балджей некоторых спиралей.

На практике после первичных редукций из кадра вычитается сглаженное изображение галактики и дальнейшие оценки флюктуаций проводят по остаточному изображению.Важной проблемой на этом этапе является правильное исключение из кадра всех артефактов, которые могут привести к неправильной оценке флюктуаций: проектирующиеся звезды фона и другие посторонние объекты, дефектные пиксели и области содержащие пыль. Получающиеся флюктуации поверхностной яркости подвергают двумерному преобразованию Фурье, что позволяет отделить шум считывания, космические частицы и дробовой шум фотонов, которые имеют спектр мощности белого шума , а также случайные флюктуации, звезды, шаровые скопления и галактики фона ,которые не были исключены из данных в силу схожести их спектра со спектром функции рассеяния точки.

Метод флюктуаций поверхностной яркости применим, в основном, к ранним типам галактик в силу двух причин:

В эллиптических и линзовидных галактиках меньше пыли, значит меньше и поглощение света;
В них, в силу большой дисперсии скоростей,не образуются структуры, подобные спиральным рукавам, которые приводят к тому, что флюктуации от пикселя к пикселю уже не являются случайными.

Для оценки флюктуаций наиболее предпочтителен фильтр I в силу двух причин:

красные гиганты наиболее ярки в этой области длин волн, что сводит к минимуму сильное влияние фона неба;
уменьшается влияние поглощения света на пыли.

Калибровка нуль-пункта M_I может проводится тремя путями:

с помощью моделирования звездного населения в галактиках;
по шаровым скоплениям Галактики;
по галактикам, принадлежащих Местной Группе.

Этот метод, дающий точность до 0.15 m , на данное время является одним из наиболее точных методов.

5. Шаровые скопления.

Эти скопления старых звезд обнаруживаются в гало всех больших галактик.Типичные шаровые скопления имеют абсолютные звездные величины M_v = -7 m (-7.5 m ), что сравнимо с яркостью сверхгигантов; а в гигантских эллиптических галактиках,которые могут содержать тысячи шаровых скоплений, ярчайшие из них могут достигать светимостей M_v

-11 m , что превышает яркость любых других звездных индикаторов расстояний (за исключением сверхновых). Они обнаруживаются на расстояниях до 100 Мпк на крупнейших наземных телескопах.

Это все делает притягательным использование их в качестве «стандартных свечей».

В настоящее время используют два метода для оценки расстояний по ШЗС:

Использование функции светимости [1];
Использование дисперсии скоростей звезд в шаровых скоплениях [6]

Последний метод применим пока только к близким галактикам Местной Группы и является аналогом соотношения Faber — Jackson для эллиптических галактик.

Характерная форма интерполяционной кривой функции светимости в виде гауссианы позволяет использовать все множество наблюдаемых шаровых скоплений для оценки расстояния до их родительской галактики, что дает больше полезной информации о расстоянии, чем несколько ярчайших скоплений. Для оценки расстояния определяют максимум функции светимости m_o, которая и является «стандартной свечей». Harris [7] показал, что абсолютная звездная величина M_o в максимуме функций светимости шаровых скоплений почти не зависит от светимости родительской галактики. Замечательным фактом является отсутствие различий между M_o шаровых скоплений в спиральных и эллиптических галактиках. Это дает возможность использовать шаровые скопления в качестве индикаторов относительных расстояний между галактиками различных морфологических типов.

Метод предпочтительно использовать для гигантских эллиптических галактик, которые содержат больше тысячи шаровых скоплений. Большим достоинством является также то, что шаровые скопления находятся чаще всего в гало галактик и вследствие этого на оценку расстояния не накладываются ошибки за различие внутреннего покраснения, за переналожение объектов и неправильное отождествление, а также за неправильный учет наклона галактики.

Средняя точность оценки расстояния по ФСШС порядка 0.4 m для одной галактики. Предельные расстояния которые доступны с помощью этого метода, ограниченные возможностями современных наземных телескопов,порядка 50 Мпк.

6. Планетарные туманности.

Светимость молодых планетарных туманностей сравнима со светимостью ярчайших звезд и несмотря на то, что узкие интерференционные фильтры (шириной порядка 30A) в полосе [5007A] пропускают всего около 15% энергии, испускаемой этими яркими источниками,оставшаяся часть позволяет выделить их на изображениях близких галактик, в которых за счет выбора фильтра подавлены основные звезды. В больших близких галактиках таким образом можно увидеть несколько сотен планетарных туманностей, функция светимостей которых имеет область значений порядка двух звездных величин. Вид функции светимостей хорошо представляется экспоненциальным законом, с учетом того, что в области предельно слабых звездных величин часто наблюдается завал.

Метод ФСПТ в основном применяется к галактикам ранних морфологических типов, в первую очередь в силу того, что для галактик поздних морфологических типов возрастает вероятность перепутать планетарные туманности с компактными областями HII.

Этот метод сравнительно новый и еще недостаточно хорошо исследована универсальность применения функции светимостей планетарных туманностей для различных галактик, хотя уже было отмечено пока еще плохо объясняемое отсутствие значимой корреляции между ФСПТ и металличностью, а также относительным возрастом звездного населения материнской галактики. Отмечена зависимость между светимостью родительской галактики и ФСПТ [8] (аналогично сверхгигантам).

7. Новые звезды.

Основой метода оценки расстояния по новым служит зависимость между их светимостью(звездной величиной) в максимуме и скоростью убывания яркости после вспышки, открытая в 1936 году Zwicky.

Для оценки расстояния по этому методу необходимо измерить видимую звездную величину новой как можно ближе к максимуму светимости и значение скорости убывания светимости,когда яркость уменьшается на 2 звездные величины после максимума.

Суммарная ошибка оценки расстояния по кривым убывания новых составляет порядка +0.4 m .

Кроме описанного выше способа оценки расстояния в различных работах были предложены другие индикаторы расстояний, связанные с новыми, кратко описанные в [1], и дающие сходные точности:

Средняя звездная величина всех наблюденных новых в данной галактике на 15 день после максимума ( = -5.60 m +0.14 m );
Функция светимости новых: а) в максимуме светимости (близка к гауссиане); б) в минимуме между первым и повторным пиками — для соответствующих новых; в) интегральная функция светимостей новых в максимуме (линейна в широком диапазоне звездных величин и имеет практически постоянный наклон);
Зависимость между промежутком видимости новой и некоторой абсолютной звездной величиной в некоторый фиксированный момент от начала вспышки.

8. Сверхновые.

Сверхновые — чрезвычайно яркие (M_b = -19.5 m ) точечные источники и вследствие этого рассматриваются как одни из наиболее привлекательных стандартных источников для больших расстояний (порядка 50 Мпк).

Сверхновые I типа (SNeI) выделяются отсутствием водорода и гелия в их оптическом спектре и имеют подклассы Ia, Ib, Ic [9].

Относительная одинаковость кривых блеска и схожесть эволюции спектров SNeIa привели к тому, что их часто используют для определения космологических параметров H₀ и q₀ [10]. Этот тип сверхновых является к тому же ярчайшим среди остальных типов.

Вспышка SN 1987A в БМО возвратила интерес к использованию метода Baade-Wesselinka для оценки геометрического размера расширяющейся фотосферы SNeII, калибровку которого связывают с этой сверхновой (она также дала на сегодняшний момент наибольшую точность для калибровки нуль-пункта цефеид).

В принципе можно использовать и сверхновые типов Ib, Ic и II-L, но они и слабее и вспыхивают реже.

Небольшое количество зарегистрированных сверхновых не дает пока возможность оценить универсальность применимости этого метода, и улучшить точность калибровки.

Выше перечисленные методы относились в основном к чисто фотометрическим. Методы, о котором речь пойдет далее, помимо фотометрических параметров требуют наблюдений лучевых скоростей и потому их можно назвать динамическими.

9. Зависимость Талли-Фишера.

Исторически первым появился на свет метод, который в наши дни известен как метод Талли-Фишера, хотя, как указывается в [1], сходный метод применял для оценки расстояния до M31 Opik еще в 1922 году. Талли и Фишер в 1977 в своей работе [11] были первыми, кто отстаивал применимость использования для определения расстояний метода, в котором устанавливалась эмпирическая зависимость между светимостью галактики позднего типа и шириной линии 21 см (т.е. скоростью вращения галактики).

Для оценки расстояния по методу ТФ необходимо получить видимые звездные величины галактик из некоторой выборки, исправленные за поглощение света в Млечном Пути и внутреннее поглощение в каждой галактике, а также каким-либо способом измеренные скорости вращения, исправленные за наклон галактик.

Галактики, сильно наклоненные к лучу зрения, наиболее удобны для анализа расстояния по ТФ-зависимости, т.к. соответствующие поправки в ротационные скорости малы, хотя в то же время растут поправки за внутреннее поглощение (особенно сильно поглощение проявляется в фотометрической полосе B). При оценке расстояний в этой области длин волн зависимость Талли-Фишера имеет наибольшую дисперсию (>0.5) [12] вследствие:

Спиральные и иррегулярные галактики наблюдаются как в богатых скопления галактик, так и по одиночке. Метод ТФ наиболее полезен для проведения массовых статистических работ в скоплениях далеких галактик для оценки структуры Вселенной на больших расстояниях.

10. Зависимость Фабер-Джексона.

Фундамент, на основе которого был предложен метод Dn-, — корреляция между светимостью нормальных эллиптических галактик и дисперсией их центральных скоростей, открытая Фабер и Джексоном в 1976 году [13]. В последствии от светимости галактики перешли к другому связанному с ней параметру Dn, который определяется как диаметр галактики до изофоты с поверхностной яркостью в цвете B 20.75 mag/[]» [14]. Этот параметр приводит к меньшим ошибкам, чем использование полных звездных величин. Он хорошо определяется, если приближать профиль E-галактики известным законом Вакулера «r 1/4 «.

Наибольшую пользу метод может принести, если использовать его для измерений относительных расстояний между галактиками.

11. Новые методы и перспективы на будущее.

В последнее время были предложены и другие способы оценки расстояний. Вероятно, некоторые из них со временем займут соответствующее место в выше перечисленной цепочке по оценке расстояний во Вселенной. Пока же универсальность применимости этих методов недостаточно изучена и поэтому перечислим лишь некоторые из них:

на возможность использования молекулярных колец в галактиках для оценки расстояния было указано в работе [15];
в [16] предложено использовать рассеянные скопления в качестве стандартных источников;
в работах [17,18] использовались углеродные звезды для оценки расстояния до NGC 55;
по желтым сверхгигантам (YSG) оценили расстояние до NGC 4523 в статье [19].
получает все большее распространение метод гравитационного линзирования, описание которого можно найти, например в [22];
описание метода оценки расстояний на основе «эффекта Сюняева — Зельдовича» приведено в [23];
используя теоретическое предположение о гравитационной устойчивости газового диска галактики с известным распределением плотности газа и кривой вращения, Засов и Бизяев («метод Засова») предложили новый метод оценок расстояний, используя который они пришли к короткой шкале расстояний H₀ = 90 км/сек /Мпк [24].

За последнее время произошли серьезные изменения в методике оценок внегалактических расстояний: были введены новые методы, исключены некоторые старые, дающие небольшую точность (например, метод оценок расстояний по размерам областей HII), были изучены различные фотометрические поправки (например,за поглощение,за металличность, за тип и светимость родительской галактики и т.п.), статистические поправки (эффект Malmquist’а [20,21]), были пересмотрены оценки точности для разных методов и т.д. Дальнейший прогресс связан с более точной калибровкой всех «стандартных свечей», с учетом новых эффектов и зависимостей, что в основном определяется развитием как наблюдательной базы, так и продвижением теоретических исследований.

Источник