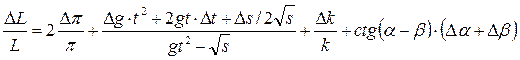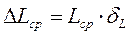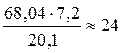Способы определения погрешности косвенных измерений
Погрешности прямых измерений. Промах. Систематическая погрешность. Случайная погрешность. Полная погрешность. Погрешности косвенных измерений. Запись результата измерений
- Оценка погрешности прямых измерений
Измерить физическую величину – это значит сравнить ее с однородной величиной, принятой за единицу меры.
Различают прямые и косвенные измерения.
Если измеряемая величина непосредственно сравнивается с мерой, то измерения называются прямыми. Например, измерения линейных размеров тел с помощью масштабной линейки и т.д.
Если измеряется не сама искомая величина, а некоторые другие величины, связанные с ней функциональной зависимостью, то измерения называются косвенными. Например, измерения объема, ускорения и т.д.
Из-за несовершенства средств и методик измерения, органов чувств при любом измерении неизбежны отклонения результатов измерений от истинных величин. Эти отклонения называются погрешностями измерений.
Погрешности измерений делятся на систематические, случайные и промахи.
1.1. Промахи, связанные с неправильными отсчетами по прибору, неправильными записями и т.д., приводят к очень большой по абсолютной величине погрешности. Они, как правило, не укладываются в общую закономерность измеренных величин. Обнаруженный промах следует отбросить.
1.2. Систематическими погрешностями Δxсист называются погрешности, которые сохраняются при повторных измерениях одной и той же величины x или изменяются по определенному закону.
Систематические погрешности подразделяются на несколько групп. Отметим только приборную погрешность.
Систематическая приборная погрешность определяется по классу точности прибора, который указывается на приборе следующими цифрами: 0,01; 0,02; 0,05; 1,0; 2,5; 4,0. Класс точности показывает предельно допустимое значение систематической погрешности, выраженной в процентах от верхнего предела на выбранном диапазоне измерений. Например, предел измерения вольтметра с классом точности 0,5 равен 200 В. Систематическая погрешность равна 0,5% от 200В. Следовательно, систематическая погрешность вольтметра равна 1 В.
Если на приборе класс точности не указан, то погрешность равна половине цены наименьшего деления шкалы прибора.
1.3. Случайными называются погрешности, которые изменяются беспорядочно при повторных измерениях одной и той же физической величины при одинаковых условиях.
Оценим случайную погрешность. Пусть при измерении какой-либо физической величины было произведено N измерений и были получены значения x1, x2, … xN. Тогда наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение
Результаты измерений x1, x2, … xN «рассеиваются» вокруг среднего. В качестве меры «рассеяния» результатов наблюдения вокруг среднего служит среднее квадратичное отклонение
Пусть a будет истинным, но неизвестным значением измеряемой величины x. Доказано, что вероятность попадания результатов измерения величины x в интервал значений от (a – S) до (a + S) оказывается равной α = 0,68.
Вероятность попадания результатов наблюдений в более широкие интервалы (a – 2S, a + 2S) и (a – 3S, a + 3S) равна α = 0,95 и α = 0,99 соответственно.
Вероятность попадания в заданный интервал значений величины x называется доверительной вероятностью, а сам интервал – доверительным интервалом.
Однако, таким образом полученный доверительный интервал справедлив при большом значении N. В учебных лабораториях, как правило, приходится ограничиваться небольшим числом измерений. В этом случае доверительный интервал находят с помощью коэффициента Стьюдента, который зависит от числа измерений N и доверительной вероятности α. В таблице 1 приведены коэффициенты Стьюдента для различного числа наблюдений при доверительных вероятностях α = 0,68; 0,95; 0,99.
Источник
Определение погрешности косвенных измерений



Погрешности измеряемых и табличных величин обуславливают погрешности DХср косвенно определяемой величины, причем наибольший вклад в DХср дают наименее точные величины, имеющие максимальную относительную погрешность d. Поэтому, для повышения точности косвенных измерений, необходимо добиваться равноточности прямых измерений
Правила нахождения погрешностей косвенных измерений:
1. Находят натуральный логарифм от заданной функции
2. Находят полный дифференциал (по всем переменным) от найденного натурального логарифма заданной функции;
3. Заменяют знак дифференциала d на знак абсолютной погрешности D;
4. Заменяют все «минусы», стоящими перед абсолютными погрешностями DА, DВ, DС, … на «плюсы».
В результате получается формула наибольшей относительной погрешности dx косвенно измеренной величины Х:
dx = 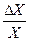
По найденной относительной погрешности dx определяют абсолютную погрешность косвенного измерения:
Результат косвенных измерений записывают в стандартном виде и изображают на числовой оси:
Пример :
Найти значения относительной и средней погрешностей физической величины L, определяемой косвенно по формуле:
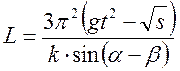
где π, g, t, k, α, β – величины, значения которых измерены или взяты из справочных таблиц и занесены в таблицу результатов измерений и табличных данных (подобную табл.1).
1. Вычисляют среднее значение Lср, подставляя в (21) средние значения из таблицы – πср , gср , tср , kср , αср , βср .
2. Определяют наибольшую относительную погрешность δL :
a). Логарифмируют формулу (21):
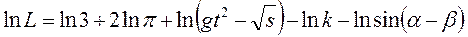
b). Дифференцируют полученное выражение (22):
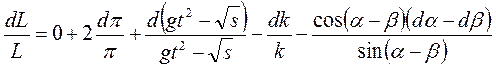
c). Заменяют знак дифференциала d на Δ, а «минусы» перед абсолютными погрешностями – на «плюсы», и получают выражение для наибольшей относительной погрешности δL :
δL =
d). Подставляя в полученное выражение средние значения входящих величин и их погрешностей из таблицы результатов измерений, вычисляют δL .
3. Затем вычисляют абсолютную погрешность ΔLср:
Результат записывают в стандартном виде и изображают графически на оси L:
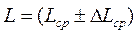
 |
2. Правила округления результатов вычисления
Результаты математических действий над приближенными числами округляют до следующего количества значащих цифр:
a) при сложении и вычитании отбрасывают значащие цифры из последних разрядов, если их нет в одном их слагаемых;
b) при умножении и делении сохраняют столько значащих цифр, сколько их в приближенном числе с наименьшим количеством этих цифр;
c) при вычислении значений функций A n , 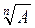
В промежуточных результатах сохраняют на одну («запасную») цифру больше.
1) 0,374 + 13,1 + 2,065 ≈ 15,5
Отброшены сотые и тысячные доли единиц, отсутствующие в числе 13,1.
2)
Оставлены две значащие цифры по их количеству в числе 7,2.
3) 216 3 ≈ 101·10 5
Оставлены три значащие цифры по их количеству в числе 216.
3. Оформление результатов прямых и косвенных измерений
Результаты измерений записывают в стандартном виде с использованием нормальной формы записи чисел, заменяя незначащие нули соответсвующей степенью десяти.
Обязательно указывается относительная погрешность измерения в процентах.
Округление конечных результатов делается по следующим правилам:
a) в среднем значении абсолютной погрешности DХср оставляют одну не нулевую значащую цифру (или две, если первая цифра – единица);
b) в среднем значении результата измерения Xср оставляют все верные цифры и одну сомнительную (две, если округленная погрешность содержит две значащие цифры).
Сомнительными считаются цифры в последних разрядах Xср , начиная с разряда, использованного для записи абсолютной погрешности DХср..
Для сравнения полученного результата с данными другого опыта или с табличным значением следует показать интервалы сравниваемых величин на числовой оси.
При частичном или полном перекрытии интервалов можно делать вывод о равенстве величин в пределах погрешности измерений.
Источник
Способы определения погрешности косвенных измерений
Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения εА равна:
При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:
В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟ 4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения) . Значение величины и погрешность следует выражать в одних и тех же единицах!
Пример оценки погрешностей косвенных измерений № 1
Пример оценки погрешностей косвенных измерений № 2
Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за топливо?
© Ивашкина Д.А., 2017. Публикация материалов с сайта разрешена только при наличии активной ссылки на главную страницу.
Источник