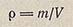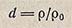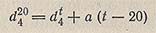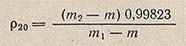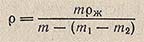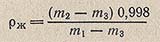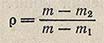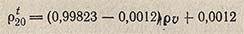Способы определения плотности твердого тела

Определение плотности

Определение плотности газов, жидкостей и твердых веществ осуществляется с целью исследования свойств веществ, идентификации и определения степени их чистоты, определения концентрации двухкомпонентных растворов спиртов, кислот и оснований.

Плотность однородного вещества р — физическая величина, равная отношению массы т вещества к занимаемому им объему V:

Единицей плотности в Международной системе единиц (СИ) является килограмм на кубический метр; в единицах СГС плотность выражается в граммах на кубический сантиметр.

Относительная плотность вещества — величина, равная отношению его плотности к плотности некоторого другого вещества при определенных физических условиях. Такими стандартными веществами служат вода при температуре 3,98 °С и нормальном атмосферном давлении (760 мм рт. ст., или 1013 гПа) или сухой воздух при 20 °С и нормальном атмосферном давлении:

где р — плотность данного вещества, р0 — плотность стандартного вещества.

Относительная плотность — безразмерная величина. Относительную плотность жидкости принято относить к температуре 20 °С и к плотности воды при 3,98 °С (4°С). В этом случае относительная плотность обозначается d204.

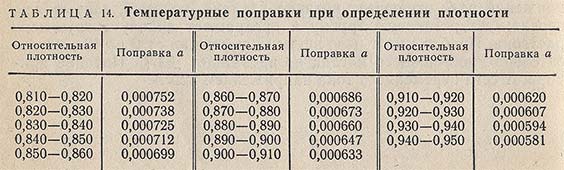
В тех случаях, когда плотность жидкости по условиям опыта определяют не при 20 °С, а при другой температуре t, ее значение dt4 может быть пересчитано на нормальное значение по формуле:

где dt4 — относительная плотность исследуемой жидкости при температуре испытания t°С; a — средняя температурная поправка на 1 °С, находимая по табл. 14.

Относительная плотность является одной из важнейших физико-химических характеристик веществ (особенно жидкостей), наряду с температурой плавления и кипения.

Плотность веществ определяют с помощью пикнометров, ареометров и гидростатических весов.

Определение плотности с помощью пикнометров

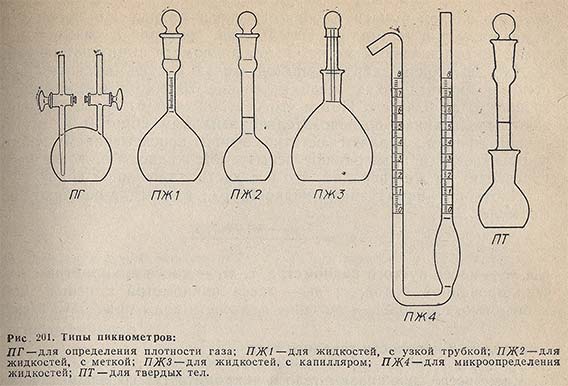
Пикнометрами можно определять плотность газов, жидкостей и твердых тел. Это стеклянные тонкостенные сосуды с меткой на горловине или с капиллярным отверстием в пробке, закрывающей горловину пикнометра. Пикнометры для определения плотности газов имеют несколько иную форму (рис. 201).

Определение плотности жидкостей

Высушенный до постоянной массы и охлажденный до комнатной температуры пикнометр взвешивают с точностью до 0,0002 г, заполняют при помощи маленькой воронки дистиллированной водой немного выше метки (пикнометры типа ПЖ1, ПЖ2 и ПЖ4) или доверху (пикнометр типа ПЖЗ). В пикнометре ПЖЗ вода выступает из капилляра, и избыток ее осторожно удаляют фильтровальной бумагой. Пикнометр закрывают пробкой и выдерживают 20 мин в водяном термостате, в котором поддерживают постоянную температуру воды 20 °С с точностью ±0,1 °С. При этой температуре уровень воды в пикнометре типа ПЖ1 или ПЖ2 доводят до метки при помощи капиллярной трубки или свернутой в трубку полоски фильтровальной бумаги. Пикнометр снова закрывают пробкой и выдерживают в термостате еще 10 мин, проверяя положение мениска по отношению к метке. Затем пикнометр вынимают из термостата, вытирают снаружи мягкой тканью досуха, оставляют под стеклом аналитических весов в течение 20 мин и взвешивают с точностью до 0,0002 г. Потом его освобождают от воды, высушивают, споласкивая последовательно этиловым спиртом и диэтиловым эфиром, удаляют остатки эфира просасыванием сухого чистого воздуха и заполняют испытуемой жидкостью, после чего производят те же операции, что и с дистиллированной водой.

Плотность испытуемой жидкости р20, в г/см3, вычисляют по формуле:

где m — масса пустого пикнометра, г; m1 — масса пикнометра с дистиллированной водой, г; m2 — масса пикнометра с испытуемой жидкостью, г; 0,99823 — значение плотности воды при 20 °С, г/см3.

Определение плотности твердого тела

Чаще всего взвешивают тело и пикнометр ПТ со вспомогательной жидкостью, налитой в него до требуемого уровня при определенной температуре, опускают тело в пикнометр с жидкостью, устанавливают жидкость на первоначальном уровне при той же температуре и взвешивают пикнометр с телом и жидкостью.

В качестве вспомогательной жидкости используют главным образом воду. Если испытуемое твердое тело растворимо в воде или взаимодействует с ней, то применяют другую жидкость (толуол, ксилол, бензин, керосин, спирт), причем предварительно ее плотность определяют описанным выше способом.

Испытуемое вещество вносят в пикнометр в виде порошка или крупных кристаллов. Для лучшего проникновения жидкости в капиллярные пустоты твердого тела рекомендуется присоединить пикнометр, содержащий испытуемое вещество и вспомогательную жидкость, к вакуумной системе и выдержать при пониженном давлении 30-40 мин.

Возможен и другой порядок определения. В качестве примера приводим определение плотности огнеупорных материалов но ГОСТ 2211-65.

Плотность огнеупоров определяют как отношение массы материала к ее объему без пор.

Пробу, измельченную до крупности зерна 0,063 мм, высушивают при 110 ±5°С до постоянной массы. Навеску материала 5-8 г засыпают в предварительно взвешенный пикнометр для твердых веществ вместимостью 25 мл.

Пикнометр с пробой взвешивают, затем до 1/2 объема наполняют вспомогательной жидкостью. Пикнометр, частично заполненный вспомогательной жидкостью и испытуемым веществом, подвергают вакуумированию не менее 30 мин. Такой же обработке под вакуумом подвергают и вспомогательную жидкость, необходимую для дополнительного заполнения пикнометра. После отключения вакуума пикнометр осторожно дополняют дегазированной вспомогательной жидкостью и помещают в термостат минимум на 30 мин. Температура в термостате должна быть 20 ±0,1°С при насыщении пробы водой и 20 ±0,2 °С при использовании ксилола и толуола. Затем уровень жидкости в пикнометре доводят точно до метки, закрывают пикнометр пробкой, вынимают его из термостата, обтирают и взвешивают.

Массу высушенного пикнометра, а также пикнометра, заполненного вспомогательной жидкостью, определяют заранее. Плотность пробы р, в г/см3, вычисляют с точностью до 0,001 г/см3 по формуле:

где m — масса пробы, г; m1 — масса пикнометра с пробой и жидкостью, г; m2 — масса пикнометра с жидкостью, г; рж — плотность вспомогательной жидкости при 20°С, г/см3 (для воды р = 0,998 г/см3).

Плотность вспомогательной жидкости вычисляют по формуле:

где m1 — масса сухого пикнометра, г; m3 — масса пикнометра с водой, г; m2 — масса пикнометра с жидкостью, г.

Определение плотности жидкости ареометрами (денсиметрами)

Применение ареометров (денсиметров) для определения относительной плотности жидкостей основано на законе Архимеда.

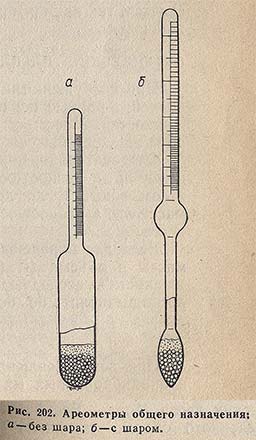
Ареометр (рис. 202) представляет собой стеклянную трубку, расширенная (нижняя) часть которой заполнена балластом — чистой и сухой металлической дробью, залитой слоем смолы с температурой плавления не ниже 80 °С. Благодаря балласту во время измерения плотности ареометр находится в вертикальном положении. На верхней части нанесена шкала. Чем меньше плотность жидкости, тем глубже погружается в нее ареометр, поэтому верхние деления шкалы соответствуют наименьшей, а нижние — наибольшей плотности. Отсчет показаний производится по нижнему мениску.

Стеклянные ареометры общего назначения, предназначаемые для измерения плотности жидкости, выпускаются со шкалами, градуированными в единицах плотности, а ареометры для измерения содержания веществ в двухкомпонентных растворах — со шкалами, градуированными в процентах растворенного вещества (по объему или по массе).

Выпускаются также ареометры специального назначения: для нефти, для морской воды, молока, для определения концентрации сухих веществ в сахаросодержащих веществах (сахарометры), для определения крепости водно-спиртовых растворов (спиртометры) и др. На шкалах специальных ареометров нанесены деления, показывающие концентрации раствора в процентах (по объему или по массе).

Сифонные ареометры используют в частности для измерения плотности электролита в аккумуляторах. Ареометр состоит из стеклянного сосуда цилиндрической или грушевидной формы. На верхнюю часть сосуда плотно насаживается резиновый шар, на нижнюю — резиновая трубка. Внутри стеклянного сосуда помещен маленький ареометр. Сжав предварительно резиновый шар, опускают резиновую трубку в аккумулятор. При разжимании шара в стеклянный сосуд всасывается электролит в количестве достаточном, чтобы ареометр мог свободно плавать.

При измерении плотности испытуемую жидкость помещают в стеклянный цилиндр для ареометров и при температуре жидкости 20 °С осторожно опускают в нее чистый сухой ареометр, на шкале которого предусмотрена ожидаемая величина плотности. Ареометр не выпускают из рук до тех пор, пока не станет очевидным, что он не тонет; при этом необходимо следить, чтобы ареометр не касался стенок и дна цилиндра. Отсчет производят через 3-4 мин после погружения по делению на шкале ареометра, соответствующему нижнему мениску жидкости (при отсчете глаз наблюдателя должен быть на уровне мениска). В случае определения плотности темноокрашенных жидкостей отсчет допускается производить по верхнему мениску.

Определение ареометром плотности летучих веществ не допускается, так как при энергичном испарении снижается температура жидкости.

Определение плотности гидростатическим взвешиванием

При погружении тела последовательно в разные жидкости оно вытеснит равные по объему, но разные по массе количества этих жидкостей. Массы этих объемов прямо пропорциональны плотностям жидкостей.

Следовательно, тело массой m в воде будет иметь кажущуюся массу m1, а разность m – m1 будет равна массе вытесненной этим телом воды. В другой жидкости тело будет иметь кажущуюся массу m2, а разность m — m2 будет равна массе вытесненной жидкости.

Если для определения плотности применять тело определенной массы и объема (стеклянный поплавок), а в качестве «другой» жидкости — исследуемую, то относительную плотность последней легко вычислить по формуле:

При использовании гидростатических весов Мора-Вестфаля, прокалиброванных с учетом определенного объема стеклянного поплавка, результат определения плотности не нужно вычислять по формуле; его сразу отсчитывают по взятому разновесу для достижения равновесия весов.

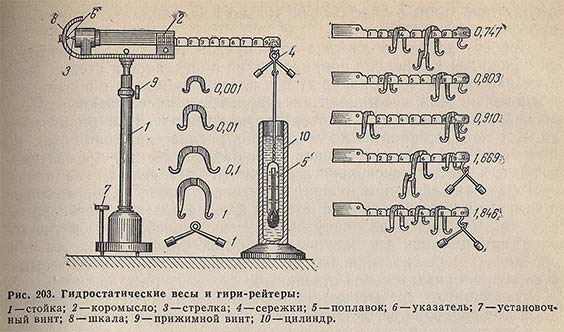
Гидростатические весы (рис. 203) состоят из неравноплечего коромысла 2, опирающегося призмой на подушку, которая заделана в вилке раздвижной колонки 1, скрепляемой прижимным винтом 9 и снабженной установочным винтом 7. На одном плече коромысла жестко укреплен постоянный противовес 3 с указателем 6 и шкалой 8, а на другом, при помощи серьги 4, к грузоприемной призме подвешен на тонкой металлической проволоке поплавок 5 с впаянным в него термометром. Плечо коромысла, несущее грузоподъемную призму, разделено на 10 равных частей углубленными нарезами, на которые навешивают специальные гири-рейтеры. Для наливания испытуемой жидкости к весам прилагается специальный стеклянный цилиндр 10. Набор разновесов состоит из нескольких рейтеров: два из них имеют массу, равную массе воды, вытесненной данным поплавком при 20 °С; другие разновески в 10, 100 и 1000 раз меньше.

Определение плотности производят на проверенных весах. Для этого металлические части весов тщательно протирают, а поплавок и проволоку промывают этиловым спиртом и диэтиловым эфиром и просушивают продуванием воздуха.

После этого, не касаясь поплавка и проволоки руками, пинцетом подвешивают их на крючок коромысла весов. С помощью установочного винта 7 колонку с коромыслом устанавливают в равновесие. Колонка при этом должна быть установлена строго вертикально. После установления равновесия весов с подвешенным поплавком в воздухе наливают в стеклянный цилиндр дистиллированную воду с температурой точно 20 °С и опускают поплавок в воду так, чтобы в воде был не только весь поплавок, но и часть проволоки (около 15 мм).

При опускании поплавка в воду нужно следить за тем, чтобы он находился в середине цилиндра, а не прикасался к стенке. При этом равновесие весов нарушится и плечо коромысла с поплавком поднимется. Для восстановления равновесия навешивают на 10-е деление коромысла (на крючок) гирю-единицу. Если равновесие не наступает, то коромысло приводят в равновесие с помощью самой маленькой гири, навешивая ее на 1-е, 2-е, 3-е или 4-е деление, если гиря-единица несколько легче, чем нужно; если гиря-единица несколько тяжелее, чем нужно, то ее навешивают на 9-е деление, а самую маленькую — на 9-е, 8-е, 7-е или 6-е деление. Установленную таким образом величину ошибки в пределах ±0,0004 учитывают при помощи отклонений коромысла, производя отсчет при определении плотности испытуемой жидкости при тех же самых отклонениях указательной стрелки. Если ошибка превышает ±0,0004, то весы подлежат ремонту. После проверки весов поплавок и цилиндр высушивают.

В чистый сухой цилиндр осторожно наливают испытуемую жидкость, пока в нее не погрузится поплавок и около 15 мм проволоки, на которую он подвешен. При этом равновесие весов нарушится и плечо с поплавком поднимется. На коромысло постепенно навешивают гири, начиная с самой крупной, пока не наступит равновесие.

Температуру жидкости измеряют или по термометру, впаянному в поплавок, или дополнительным термометром. По достижении равновесия весов и установлении температуры записывают так называемую «видимую» плотность испытуемой жидкости, начиная с гири-единицы.

«Видимую» плотность р’ пересчитывают в действительную плотность р по формуле:

где 0,99823 — значение плотности воды при 20 °С; 0,0012 — значение плотности воздуха при 20 °С и барометрическом давлении 760 мм рт. ст. (1013 гПа).

Источник

ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ РАЗНЫМИ МЕТОДАМИ

Ознакомится с методами измерения физических величин проводимых измерений на примере определения плотности твердых тел.

Скачать:

Вложение	Размер
nou_plotnost.doc	268.5 КБ

Предварительный просмотр:

III Ашинский районный конкурс реферативно-исследовательских работ

для учащихся 5-8 классов

Определение плотности твердых тел

Авторы: Фокин Дмитрий, Зарипов Юлиан

7 «А» класс МКОУ СОШ №1 г. Миньяра Руководитель: Лактионова Надежда

Сергеевна, учитель физики

2. Основная часть

2.1. Аппаратура и метод измерений. 4-6

2.2. Определение плотности твердых тел.……………………………. 6-7

2.2.3. Метод безразличного плавания………………………………..10-12 3. Заключение …………………………………….…………………………….12

Что значит измерить физическую величину правильно? На этот вопрос ответить непросто. Обычно смешивают два понятия: правильно и точно. «Часто стараются произвести измерения с наибольшей достижимой точностью, т.е. сделать ошибку измерений по возможности малой. Однако следует иметь в виду, что чем точнее мы хотим измерить, тем труднее это сделать. Поэтому не следует требовать от измерений большей точности, чем это необходимо для решения поставленной задачи .

Я ставлю перед собой задачу определить плотности твердых тел различными методами, сравнить полученные результаты с табличными и убедиться в том, что проводимый нами эксперимент дает небольшую ошибку. Для чего нужно знать плотность вещества? Плотность вещества нужно знать для различных практических целей. Инженер, создавая машину, заранее по плотности и объему материала может рассчитать массу деталей будущей машины. Строитель может определить, какова будет масса строящегося здания. Так, если океанологам известно вертикальное распределение плотности морской воды, то они могут рассчитать направление и скорость течений. Вертикальное распределение плотности необходимо знать и для определения устойчивости водной массы: если масса неустойчива, то есть если более плотная вода лежит выше менее плотной, будет происходить перемешивание. Даже в домашних условиях при покупке ковролина следует обратить внимание на плотность ворса. Ковролин высокой плотности прослужит дольше, и на нем не будут оставаться вмятины от мебельных ножек.

Цель работы: ознакомится с методами измерения физических величин проводимых измерений на примере определения плотности твердых тел.

2. Основная часть

2.1. Аппаратура и метод измерений

Для оценки плотности твердого тела необходимо знать его объем и массу. Массу тела можно определить взвешиванием его на рычажных весах. Объем тела правильной геометрической формы определяют, измеряя его линейные параметры. Таким образом, чтобы узнать плотность тела, необходимо провести ряд физических измерений. Под измерением понимается сравнение измеряемой величины с другой величиной, принятой за единицу измерения.

Измерения делятся на прямые и косвенные. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно с помощью измерительного прибора, проградуированного в соответствующих единицах. Примерами прямых измерений могут служить измерения длин линейкой, промежутков времени секундомером. При косвенных измерениях искомое значение величины не измеряется непосредственно, а находится по известной зависимости между этой величиной и величинами, полученными при прямых измерениях. К косвенным относятся, например, измерения объема, плотности твердых тел, измерение скорости движения тела по измерениям отрезков пути и промежутков времени, измерение удельного сопротивления проволоки. Никакая физическая величина не может быть, однако, определена с абсолютной точностью. Другими словами, любое измерение всегда производится с некоторой ошибкой — погрешностью. Поэтому полученное в

результате измерений значение какой-либо величины должно быть записано в виде x ± Δ x, (1)

где Δ x — абсолютная погрешность измерения, характеризующая возможное отклонение измеренного значения данной величины от его истинного значения. При этом, поскольку истинное значение остается неизвестным, можно дать лишь приближенную оценку абсолютной погрешности. Поскольку причины возникновения ошибок бывают самыми разными, необходимо классифицировать погрешности. Только тогда возможна их правильная оценка, так как от типа погрешностей зависит и способ их вычисления.

Погрешности подразделяются на случайные и систематические. Систематической погрешностью называют составляющую погрешности измерения, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины. Она может быть связана с неисправностями измерительных приборов, неточностью их регулировки, неправильной их установкой. Систематические погрешности в принципе могут быть исключены, поскольку причины, их вызывающие, в большинстве случаев известны.

Случайной погрешностью называют составляющую погрешности измерения, изменяющуюся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности зависят от условий, в которых производятся измерения, от специфики измеряемых объектов. Эти погрешности принципиально неустранимы, однако их величина уменьшается при использовании многократных измерений. Выделяют также погрешности приборов, которые могут иметь как систематический, так и случайный характер. Эти погрешности связаны с несовершенством любого (исправного) измерительного инструмента. Если значение измеряемой величины определяется по шкале инструмента, абсолютная погрешность прибора считается, как правило, равной половине цены деления шкалы (например, линейки) или цене деления шкалы, если стрелка прибора перемещается скачком (секундомер).

Как уже указывалось, случайные погрешности можно уменьшить, многократно измеряя одну и ту же величину. Однако максимально возможная точность измерения определяется теми приборами, которые используются в эксперименте. Поэтому увеличение числа измерений имеет смысл лишь до тех пор, пока случайная погрешность не станет явно меньше погрешности прибора. Для правильной записи конечного результата необходимо округлить рассчитанное значение абсолютной погрешности и сам результат измерения. Как правило, точность оценки погрешности бывает очень небольшой.

Поэтому абсолютная погрешность округляется до одной значащей цифры.

Если, однако, эта цифра оказалась единицей, следует оставить две значащие цифры. Округление конечного результата производится с учетом его погрешности. При этом последняя значащая цифра результата должна быть того же порядка величины (находится в той же десятичной позиции), что и погрешность. Если, к примеру, получено, что ρ = 8723 , 23 кг / м3, а

Δ ρ = 93 , 27 кг / м3,

то правильная запись результата будет выглядеть так

ρ = (8720 ± 90) кг / м3 .

2.2.Определение плотности твердых тел

Тела, изготовленные из различных веществ, при одинаковой массе имеют разные объемы. Железный брус массой 1 т имеет объем 0,13 м 3 , а лед массой 1 т – объем 1,1 м 3 , т.е. почти в 9 раз больше.

Из этих примеров можно сделать и такой вывод, что тела объемом 1 м3 каждое, изготовленные из различных веществ, имеют разные массы. Железо объемом 1 м 3 имеет массу 7800 кг, а лед того же объема – 900 кг, т.е. почти в 9 раз меньше. Это различие объясняется тем, что различные вещества имеют разную плотность. Плотность показывает, чему равна масса вещества, взятого в объеме 1 м 3 .

Плотность – физическая величина, характеризующая свойство тел равного объема иметь разную массу.

Чтобы определить плотность вещества, надо массу тела разделить на его объем. Следовательно, плотность есть физическая величина, равная отношению массы тела к его объему.

Единицей плотности вещества является . Это плотность однородного вещества, масса которого равна 1 кг при объеме 1 м 3 .

2.2.1. Метод Менделеева

Метод Менделеева (метод взвешивания). На одну чашку весов кладется гиря с массой заведомо большей, чем масса тела, а на другую — разновесы, добиваясь равновесия весов. Затем на чашку с разновесами помещают взвешиваемое тело, а разновесы снимают до тех пор, пока вновь не установится равновесие. Масса снятых гирь будет равна массе тела. Этот метод позволяет исключить систематические погрешности, связанные с неравноплечностью весов и зависимостью их чувствительности от величины нагрузки.

Порядок выполнения работы:

1. С помощью линейки определить размеры исследуемого тела, необходимые для вычисления его объема. Каждый параметр измерить не менее пяти раз.

2. С помощью весов и разновесов определить массу тела. Взвешивание производить не менее пяти раз.

3. Все экспериментальные результаты занести в таблицу.

Обработка результатов измерений

1. По полученным экспериментальным данным находят средние значения линейных размеров и массы тела.

2. Используя средние значения замеренных параметров, вычисляют

плотность изучаемого тела.

3. Определяют абсолютную погрешность Δ ρ . Записывают окончательный результат измерения плотности тела, используя правила округления погрешностей и самой измеряемой величины.

Источник