Способы определения площадей земельных участков геодезия

Cпособы определения площадей в геодезии

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей.

1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).

2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте). Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.

3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) участки разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам — высотам и основаниям.

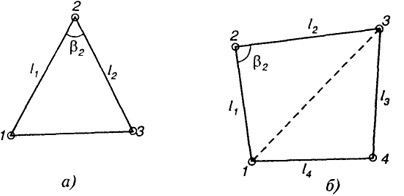
Рис. 23.1. Геометрические фигуры для определения площадей участков (а, б)

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков (рис. 23.1).

Треугольник (рис. 23.1, а). Площадь треугольника определяется по сторонам l₁ и l₂, углу β₂, заключенному между ними, по формуле

Четырехугольник (рис. 23.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1 — 2 — 3 может быть вычислена по формуле (23.1). При этом полезно вычислить длину l_1-3, используя теорему косинусов

Площадь треугольника 1 — 3 — 4 может быть вычислена по формуле

где S — полупериметр, равный

Общая площадь четырехугольника будет равна:

Источник

Способы определения площади земельного участка

При проведении землеустроительных работ используются различные способы вычисления площадей участков земли. Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.

Основные способы

Существует три основных способа определения площадей:

• аналитический;
• графический;
• механический.

При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства — планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

• Xi и Yi — координаты i-той характерной точки участка, имеющего вид многоугольника;
• i — порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n — число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

• a и b — основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

a,b,c,d — величины сторон.

Тогда площадь участка Sу будет равна:

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.

Механический способ

Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.

Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
Точность метода зависит от размеров участка и свойств плана.

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность — это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

• mt — СКП расположения поворотных точек;
• P — площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

При покупке квартиры можно получить налоговый вычет. Подробнее об этом читайте в нашей статье.

Хотите оформить в собственность участок, взятый в аренду на 49 лет? Здесь есть подробная инструкция.

Определение площади участка на ПКК

Публичная кадастровая карта (ПКК) — это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).

Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.

Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.

Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: «обл. Московская, р-н Зарайский, снт «Изобретатель», уч-к 116″.

Однако при обращении к ПКК с использованием этого адреса система дает сбой. Подобный результат получается и при обращении к ПКК на других страницах.

Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.

Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.

Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.

По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.

Источник

Способы определения площадей

Характеристика главных преимуществ и недостатков графического, аналитического и механического способов определения площадей. Изучение влияния деформации бумаги. Исследование основных ошибок при определении площади по результатам измерения на местности.

Рубрика	Геология, гидрология и геодезия
Вид	курсовая работа
Язык	русский
Дата добавления	04.06.2014
Размер файла	401,9 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru

1. Способы определения площадей

1.1 Графический способ определения площадей

1.2 Аналитический способ определения площадей

1.3 Механический способ определения площадей

2. Точность определения площадей

2.1 Исследование ошибок определения площади по результатам измерения на местности

2.2 Исследование ошибок определения площади по плану и влияние деформации бумаги

2.2.1 Ошибки определения площадей графическим способом

2.2.2 Ошибки определения площадей палетками

2.2.3 Деформация бумаги и ее учет при определении площадей

Список используемой литературы

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра. В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют следующие способы определения площадей.

Аналитический способ — площадь вычисляется по результатам вычисления координат вершин фигур или по формулам геометрии (при разбивке участка на правильные геометрические фигуры).

Графический способ — площадь вычисляется по карте, используя формулы простых фигур, на которые разбивается участок, или палеткой.

Механический способ — площадь определяется по плану или карте с помощью специального прибора (планиметра).

В данной работе рассматриваются способы определения площадей и анализируется каждый из них на примере выбранного участка, для сравнения точности вычислений.

графический местность площадь

1. Способы определения площадей

При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам. Измерение площадей на планах и картах необходимо для решения различных инженерных задач.

Существует три основных способа определения площадей: графический, когда площадь вычисляется по данным, взятым графически с плана или карты; аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям — координатам вершин участка; механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.

1.1 Графический способ определения площадей

Данный способ заключается в том, что определенный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже — прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры. Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка.

Площади криволинейных контуров удобно определять при помощи палеток. Палетки бывают прямолинейные и криволинейные. К прямолинейным относятся квадратные и параллельные палетки. К криволинейным относятся гиперболические палетки, представляющие систему гиперболических кривых и применяющиеся для определения площадей простейших геометрических фигур. Однако гиперболические палетки применяются редко, так как они не пригодны для быстрого определения площадей с криволинейными контурами.

Палетка (рисунок 1) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура. Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Квадратная палетка представляет сеть взаимно перпендикулярных линий, проведенных через 1-2мм на прозрачном материале. Для упрощения подсчетов количества клеток проводят утолщенные линии через 0,5см и 1см, чтобы подсчитать клетки группами — в 25 и 100 мм2.

Недостатком квадратной палетки является то, что площади долей квадратиков, рассекаемых контуром, берутся на глаз и то что, подсчет целых квадратиков или их долей сопровождался ошибками.

Недостаток квадратной палетки заключается в том, что площади долей клеток оцениваются на глаз, а подсчет целых клеток может сопровождаться ошибками, поэтому не рекомендуется такой палеткой определять площади больше 2 см2на плане.

Отмеченных выше недостатков квадратной палетки не наблюдается при определении площадей параллельной палеткой, представляющей собой лист прозрачного материала, на котором нанесены параллельные линии, в основном через 2 мм одна от другой (рис. 1.2).

Площадь контура этой палеткой определяют следующим образом. Накладывают ее на контур так, чтобы крайние точки a и b разместились посередине между параллельными линиями палетки. Тогда весь контур окажется расчлененным параллельными линиями на фигуры, близкие к трапециям с одинаковыми высотами, причем отрезки параллельных линий внутри контура являются средними линиями трапеций. На рисунке 1.2 прерывистыми линиями показаны основания этих трапеций. Площадь контура будет равна сумме площадей трапеций:

P = cd h + ef h + mn h + … +kl h (1)

P = h( cd + ef + mn + … + kl), (1.2)

так как высоты в фигурах равны.

Таким образом, чтобы определить площадь контура, следует взять сумму средних линий, то есть сумму отрезков параллельных прямых, проходящих внутри контура, и умножить на расстояние между ними. Параллельная палетка предназначена для определения площадей небольших контуров, при этом не рекомендуется определять ей площади больше 10 см2на плане.

Ошибка определения площади графическим способом равна примерно 1:100 — 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.

1.2 Аналитический способ определения площадей

Площади вычисляют по результатам измерений линий и углов на местности с применением формул геометрии, тригонометрии и аналитической геометрии.Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.Если по результатам измерений на местности определены координаты вершин замкнутого многоугольника, то его площадь может быть определена аналитическим способом. Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 2), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 2 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:

Р = 0,5 [(Х1 + Х2) (Y2 — Y1) + (X2 + X3) (Y3 — Y2) — (X3 + X4) (Y3 — Y4) — (X4 + X1) (Y4 — Y1)]. (2)

Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:

2Р = Х1(Y2 — Y4) + X2(Y3 — Y1) + X3(Y4 — Y2) + X4(Y1 — Y3)

или в общем виде для n-угольника можно записать

2Р= УХi(Yi+1 — Yi-1). (2.1)

Подобным образом из уравнения (1.1) после преобразований можно получить:

2Р= Y1(X4 — X2) + Y3(X1 — X3) + Y3(X2 — X4) + Y4(X3 — X1)

2Р = УYi(Хi-1 — Xi+1). (2.2)

Согласно формулам (2.1) и (2.2) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.

Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (2.1) и (2.2).

Погрешность вычислений площадей аналитическим способом не превышает 1:1000 вычисляемой площади.

1.3 Механический способ определения площадей

Определение площадей механическим способом производится при помощи планиметров. Планиметрами называют механические приборы, позволяющие путем обвода плоской фигуры любой формы определить ее площадь. Планиметры бывают различных систем и подразделяются на линейные и полярные. Наибольшее распространение получили полярные планиметры, состоящие из двух рычагов — обводного и полюсного, соединенных шарниром, а также счетного механизма с делениями.

Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом — штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.

Рисунок 3 Полярный планиметр: 1 — полюсный рычаг; 2 — обводной рычаг; 3 — обводной шпиль или лупа; 4 — счетное устройство; 5 — счетное колесо; 6 — циферблат; 7 — указатель циферблата; 8 — верньер

Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья — по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3 составит 3215.

При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Рпри полюсе вне фигуры вычисляют по формуле:

а при полюсе внутри фигуры

Р= С(U2 — U1 + g), (3.1)

Где С- цена деления планиметра; g — постоянное число планиметра.

Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число. При проверке планиметра должны быть проверено выполнение следующих условий:

счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний.

Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.

плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага.

Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.

Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры. Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:

С = Р/ (U2 — U1)ср. (3.2)

После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры. Постоянное число планиметра:

g = P/C — (U2 — U1). (3.3)

При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.

При определении площадей планиметром необходимо соблюдать следующие правила:

план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;

положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;

обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;

для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.

Точность определения площадей планиметром зависит от формы и размеров обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10 — 30 см2) ошибка определения площади планиметром не превышает 1:200 величины площади.

2. Точность определения площадей

2.1 Исследование ошибок определения площади по результатам измерения на местности

В зависимости от хозяйственной значимости участков и массивов, их размеров, конфигурации и вытянутости, наличия планово-топографического материала, топографических условий местности применяются следующие способы определения площадей:

Аналитический — когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур);

Графический — когда площадь вычисляется по результатам измерений линий на плане (карте);

Механический — когда площадь определяется по плану при помощи специальных приборов (планиметров) и приспособлений (палеток) и других.

Иногда эти способы применяются комбинированно, например, часть линейных величин для вычисления площади определяется по плану, а часть берут из результатов измерений на местности. Нередко основная площадь участка, заключенная в теодолитный полигон, определяется аналитическим способом, а площадь, выходящая за пределы полигона и заключенная между линиями полигона и живого урочища, определяется графическим или механическим способом.

Наиболее точным является аналитический способ, поскольку на точность определения площади этим способом влияют только погрешности измерений на местности, в то время как с применением графического и механического способов, помимо погрешностей измерений на местности, влияют погрешности составления плана, определения площадей по плану и деформация бумаги. Однако аналитический способ требует измерения линий и углов по границам участков, больших вычислительных действий, зависящих от количества углов. Целесообразно применять аналитический способ, если число углов по границе участка невелико (не более 10—15).

Наименее точным, но наиболее распространенным является механический способ, так как, пользуясь им, можно быстро и просто определять по плану площадь участка любой формы.

Графический способ выгодно применять в том случае, когда границей участка является ломаная линия с небольшим числом поворотов.

Если площадь фигуры определяется по результатам непосредственных измерений на местности, то можно выполнить предрасчет точности площади по формулам теории ошибок. Ошибки площадей полигонов различной формы вычисляются по таким формулам:

Средняя квадратическая ошибка площади, имеющую форму правильного многоугольника, вычисляется так:

Подставим значение n в эту формулу для таких форм многоугольника:

Из этого видно, что самой оптимальной формой многоугольника является треугольник.

Средняя квадратическая ошибка площади полигона (участка), которая имеет форму параллелограмма целесообразно находить по такой формуле:

где — средняя квадратическая ошибка единицы веса; l — значения линий; — внутренние углы

По данной формуле можно получить такие формулы ошибок площадей:

Для прямоугольника с соотношением сторон, равным и :

Если полигон имеет изогнутую форму, то формула ошибки для данного случая будет такова:

2.2 Исследование ошибок определения площади по плану и влияние деформации бумаги

2.2.1 Ошибки определения площадей графическим способом

Графический способ вычисления площадей состоит в том, что участок, изображенный на плане, разбивают на простейшие геометрические фигуры (треугольники, прямоугольники, трапеции). В каждой фигуре на плане измеряют высоту и основание, по которым вычисляют площадь, и сумма площадей фигур дает площадь участка.

Если участок разбит на треугольники, то площадь каждого треугольника равна:

Для получения зависимости между относительными средними квадратическими ошибками площади и измерений основания и высоты необходимо прологарифмировать выражение (4):

lnP = lnl + lnh — ln2

Дифференцируя по переменам l и h , получаем:

Относительная средняя квадратическая ошибка площади треугольника равна:

Такую же зависимость можно получить для прямоугольника, параллелограмма, ромба и трапеции, если их площадь вычисляется по основанию и высоте (площадь трапеции по средней линии и высоте).

Ошибки измерения по плану можно считать одинаковыми независимо от длин линий:

Основание определяется несколько точнее высоты, потому что на определение высоты, помимо ошибки определения на плане, влияет также ошибка проведения основания между вершинами углов, до которого измеряется высота. Однако влияние этой ошибки на ошибку определения высоты невелико, если треугольник равнобедренный. Если же треугольник близок к прямоугольному, то ошибка высоты в 1,2 раза больше ошибки основания. Тогда получаем:

Так как для треугольника lh = 2P , а для остальных фигур lh = P , то получим:

Для прямоугольника, параллелограмма и трапеции:

Если участок разбивается на треугольники, у которых высоты примерно равны основаниями, то ошибка площади участка вычисляется по формуле:

где m — ошибка определения расстояния по плану.

А для прямоугольника (по форме близкого к квадрату), параллелограмма и трапеции:

Таким образом, площадь треугольника графическим способом вычисляется точнее площадей других фигур, следовательно, разбивкой участка на треугольники вычисляется площадь точнее, чем разбивкой на прямоугольники, трапеции и другие фигуры.

2.2.2 Ошибки определения площадей палетками

Для определения площадей мелких контуров применяют различного рода палетки. Наиболее удобными для пользования и построения являются квадратная и параллельная палетки.

При оценке точности определения площадей палетками принимается во внимание, что ими определяют площади криволинейных контуров, так как площадь участка, ограниченного прямыми линиями, быстрее и точнее можно определить графическим способом.

Палетками определяют площади небольших контуров, не превышающих 10см2 (с.к.о. или m = 0,03).

Таким образом, зависимость ошибки площади от ее величины, определяемой квадратной палеткой, выражается формулой:

Для различных масштабов планов эту формулу можно записать так:

где M — знаменатель численного масштаба плана; P — площадь участка (га).

2.2.3 Деформация бумаги и ее учет при определении площадей

При определении площадей по плану графическим способом необходимо учитывать деформацию бумаги (плана). Величина деформации может характеризоваться коэффициентами, определяемыми в двух взаимно перпендикулярных направлениях, по формуле:

где l0 — теоретическая длина линии, значащаяся на плане; l — результат измерения этой линии по плану.

Коэффициент деформации бывает 1: 400, 1: 200, 1: 100 и 1: 50. Величина его зависит от сортов бумаги, условий хранения плана, погоды, времени, которое прошло с момента составления плана. Копии с планшетов, отпечатанные на машине, деформируются во время печатания, причем в направлении движения бумага растягивается, а в поперечном направлении сжимается. Через некоторое время деформация бумаги несколько уменьшается, но все же остается значительной.

Особенно сильно деформируется бумага от частого свертывания ее в трубку или складывания вдвое, вчетверо. Если бумага деформируется равномерно, то есть в двух взаимно перпендикулярных направлениях одинаково, то учет деформации не представляет трудности и, наоборот, при неравномерной деформации затрудняется учет, если линия направлена под углом к линиям координатной сетки.

В связи с необходимостью учета деформации бумаги приходится в линии, определенные по плану для вычисления площади, вводить поправки.

Пусть l — результат измерения линии на деформировавшемся плане. Для того чтобы определить соответствующее ей горизонтальное проложение на местности l0, необходимо ввести поправку за деформацию бумаги. Пусть коэффициенты деформации в двух взаимно перпендикулярных направлениях будут различными: qx и qy. Выполнив ряд преобразований, получим:

Если qx и qy или расхождения между ними составляют 20%, то можно принять средний коэффициент деформации q, тогда получим формулу:

где lq — поправка к линии l за деформацию бумаги.

Если поправка в линию меньше точности масштаба (или меньше 0,08мм на плане), то ее можно не вводить в результат измерения линии по плану. По линиям, исправленным за деформацию бумаги, можно вычислять площади фигур. Также, можно определить поправки в площади фигур, полученные по результатам измерений линий на деформировавшемся плане, по таким формулам:

где P(qx + qy) — поправка в площадь за деформацию бумаги.

Если коэффициенты равны qx = qy = q или вычислен средний коэффициент:

При определении площадей графическим способом, когда участок разбивается на простейшие геометрические фигуры, не целесообразно вводить поправку в площадь каждой из этих фигур, а необходимо исправить общую площадь участка за деформацию бумаги.

В данной работе я рассмотрела способы определения площадей земельных участков: графический, аналитический и механический. Определила с их помощью площадь выбранного участка. Оказалось, что самым точным является аналитический способ, самым же неточным графический. Аналитический способ более трудоемкий, по сравнению с графическим и механическим.

Список используемой литературы

1. И.Ф. Куштин, В. И. Куштин. Инженерная геодезия. Ростов-на-Дону: Изд. ФЕНИКС, 2002. — 416 с;

2. М. И. Киселев, Д. Ш. Михелев. Инженерная геодезия. М.: Изд. «Академия», 2007. — 480 с;

3. А. В. Маслов, А. В. Гордеев, Ю. Г. Батраков. Геодезия. М.: КолосС, 2006. — 599 с.

4. А.В. Никитин. Определение площадей земельных участков: Учеб. пособие — Хабаровск: Изд-во ДВГУПС, 2003. — 60 с.

Определение площади участка графическим способом

Площадь участка определяем при помощи палетки, на которой разбита сетка квадратов со стороной 2мм. Мы прикладываем палетку таким образом, чтобы весь участок был внутри квадрата. Затем производим подсчет сначала целых квадратов внутри участка, а затем складывают неполные квадраты, оценивая их в частях полных, в результате площадь равна произведению площади одного квадрата на число всех квадратов.

Где n — это число всех квадратов

Определение площади участка механическим способом

Определяем цену деления планиметра путем обвода несколько раз границы квадрата со стороной 10 см. При этом снимаем отсчет с планиметра и записываем его. По данной формуле определяется цена деления планиметра:

Где S- это площадь квадрата, — это разность отсчетов по планиметру.

Источник