Способы определения параметров четырехполюсников

Четырехполюсники, их классификация. Уравнения пассивных четырехполюсников, способы определения их параметров (показать на примерах).

Четырехполюсники. Их классификация.

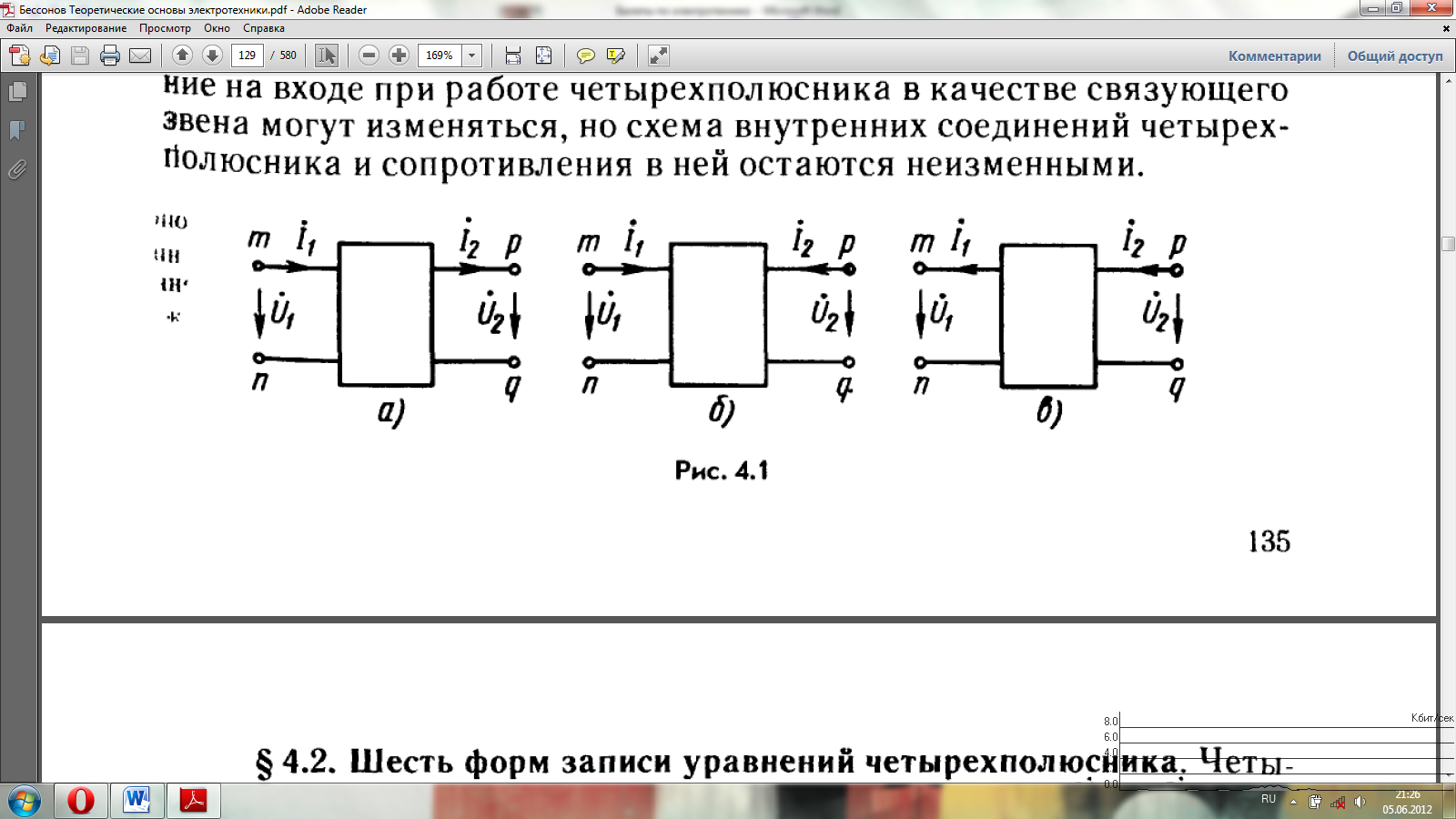
Ч 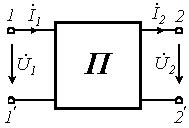етырехполюсник – часть ЭЦ, имеющ. две пары выводов для подключения к источнику и приемнику эл. энергии.(эл. фильтр, усилитель, трансформатор)

Выводы (1,1’) – входные, (2,2’) – выходные.

1.Линейные и нелинейные (признак линейности входящих в них элементов)

2.Активные и пассивные (активные – содерж. внутри источники энергии, пассивные – не содерж.)

3.Симметрич. и несимметрич. (симметрич. – перемена местами вх. и вых. выводов не изменяет токов и напряжений в цепи, с ктр. он соединен; иначе — несимметрич.)

4.Обратимые и необратимые (обратимые — выполняется теор. обратимости: отношение напряж. на входе к току на выходе не зависит от того какая из двух пар выводов является вход. и выход.)

Определение параметров четырехполюсников. Схема четырехполюсника задана.

Составляем уравнения по Кирхгофу и приводи к виду форм

Из режима х.х. и к.з. Режим хх (I₂=0): ; Режим кз (U₁=0):

Представление цепи в виде простых четырехполюсников, параметры которых уже известны

Схема четырехполюсника не задана.

Экспериментальное определение параметров 4-пол-ов

Для опытного определения параметров 4-ка проводят измерения при холостом ходе, когда , и при коротком замыкании, когда и .

Рассмотрим основные уравнения 4-ка в случае холостого хода при питании первич. зажим.: ; 1) , . 2) .

(1).

2) , , , (2).

Для симметричного 4-ка измерить сопротивление и достаточно, так как имеют место связи: (3), (4).

В случае несимметричного 4-ка , , надо выполнить 1-ый опыт, произвести измерения на стороне вторичных зажимов (при холостом ходе на первичных зажимах), либо при коротком замыкании на первичных зажимах.

При этом рассмотрим уравнение при обратном питании: — со стороны вторичных зажимов.

ХХ со стороны вторичных зажимов: . .

Совместим решения уравнений: , , , условия пассивности: окончательно даёт .

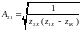
Если проведём опыт короткого замыкания при питании со стороны вторичных зажимов, из которого известно , в начале определяем : .

Во всех 3-х случаях провести не менее 3 опытов.

Схемы замещения (канонические) пассивных четырехполюсников. Связь параметров четырехполюсников с сопротивлениями т- и п- образной схемы замещения.

Схема замещения четырехполюсника.

Так как пассивный 4-пол-к характеризуется тремя независимыми параметрами, то прост. схема замещения 4-пол-ка содержит 3 элемента. Наиболее распространены Т и П-образные схемы замещения.

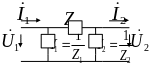
Установим связь между парами элементов схемы замещения и коэф. формы

Т-образная схема замещения

1)

2)

3)

Подставляем из (3) в (1) и сравниваем получ. уравнение с уравнениями в форме : где = , =

где и

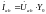
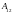
Пар. Т-образной схемы замещения можно выразить через

, ,

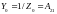
Для П-образных схем:

, ,

,

Для симметрич. 4-пол-ков:

Под физически реализуемой схемой понимается схема, в которой параметры

Входные сопротивления и передаточные коэффициенты 4-хполюсников. Согласование четырехполюсников. Характеристические параметры симметричных четырехполюсников.

Входное сопротивление 4 –пол-ка при произвольной нагрузке.

при обр. питаниии

еакцию 4-пол-ка при произв. нагрузке исследуем с помощью системы уравнений формы :

Если рассмотреть 4-к вместе с нагрузкой, как 2-к, то при прямом питании: .

При обратном питании: .

При симметричном 4-ке: .

Поскольку входные сопротивления 4-ка является дробно-линейными функциями сопротивления

нагрузки, то это позволяет использовать 4-к в качестве трансформатора сопротивлений, в том числе для согласованного источника с нагрузкой.

Уравнение симметричного 4-пол-ка в гиперболич. форме

Характеристические параметры: характеристическое сопротивление и .

Уравнение симметричного 4-ка в гиперболической форме.

Для записи уравнения 4-ка удобно пользоваться гиперболическими формулами:

, , (1).

Уравнение (1) сходное с условиями пассив.:

(2)

Сравнив (1) и (2) получаем: ,

Пусть — характеристическое сопротивление симметричного 4-ка. — входное сопротивление 4-ка при ХХ на вторичных зажимах, — входное сопротивление 4-ка при КЗ на вторичных зажимах. Из опытов ХХ и КЗ: , , .

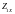
Все коэффициенты формы симметричного 4-ка можно выразить через , , .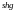

(без размерн), (Ом), (См).

Уравнение симметричного 4-ка в гиперболической форме:

,

. (4)

, .

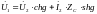
Из уравнений для симметричного 4-ка следует, что только 2 величины 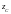и определяют условия передачи энергии через симметричный 4-к.

Физический смысл основных характеристик 4-пол-ка

Во многих случаях осуществляется согласованный выход сопротивления 4-ка с сопротивлением нагрузки и входным сопротивлением 4-ка с сопротивлением источника напряжения или ЭДС.

В общем случае для несимметричного 4-ка положим, что выходное сопротивление подобрано так, что , то есть равно характеристическому сопротивлению . .

Условия, когда 4-к нагружен соотв. характеристическим сопротивлением называется условием согласованной нагрузки.

Для симметричного 4-ка: , — повт. сопротивление.

Пусть для симметричного 4-ка задан режим согласованной нагрузки: , .

Уравнения 4-ка имеют вид

Из второго: .

, , , .

Величина g называется мерой передачи: а – коэффициент затухания, b – коэффициент фазы.

«а» показывает на сколько изменится при переходе через симметричный 4-к по модулю U и I. «b» — на сколько изменится фаза напряжения или тока при переходе через 4-к. Для несимметричного 4-ка при согласованной нагрузке , , тогда g получается, как половина натурального логарифма отношение произведений комплексных U и I на входе и выходе 4-ка при согласованной нагрузке — для нессиметричного.

, .

;

Для симметричного 4-ка при согласованной нагрузке: .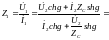

Таким образом, если на выходе 4-ка симметрично подключить характерное сопротивление , то его входное сопротивление также равно , в этом случае характерное сопротивление называют повторным сопротивлением.

Источник