Как определить частоту по фигуре Лиссажу.
В одной из прошлых статей описывалось как определить разность фаз двух сигналов по фигуре Лиссажу. Но у фигур Лиссажу есть ещё одно интересное свойство и заключается оно в следующем: если известна частота одного из колебаний, то по виду фигуры Лиссажу можно определить частоту другого.
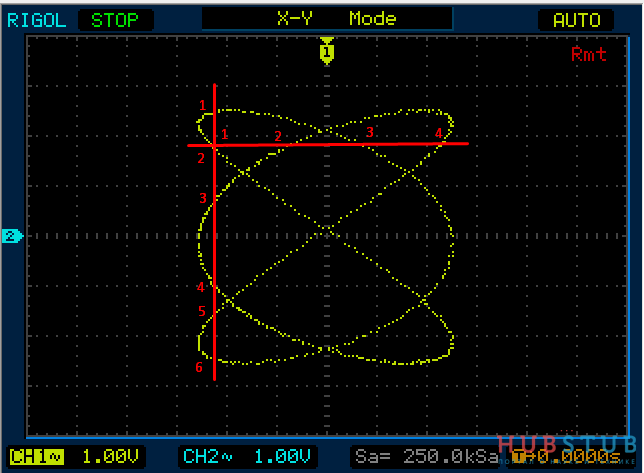
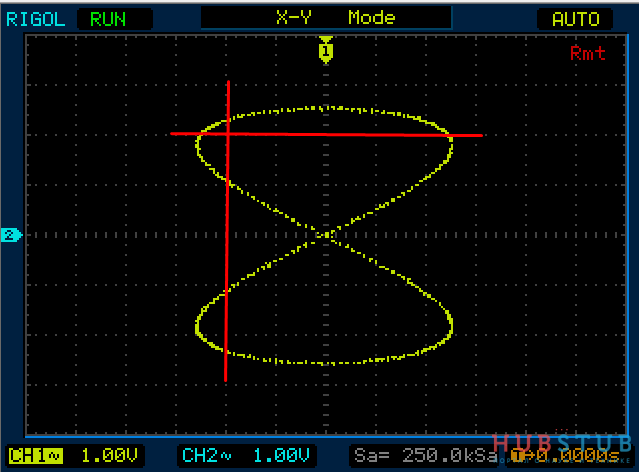
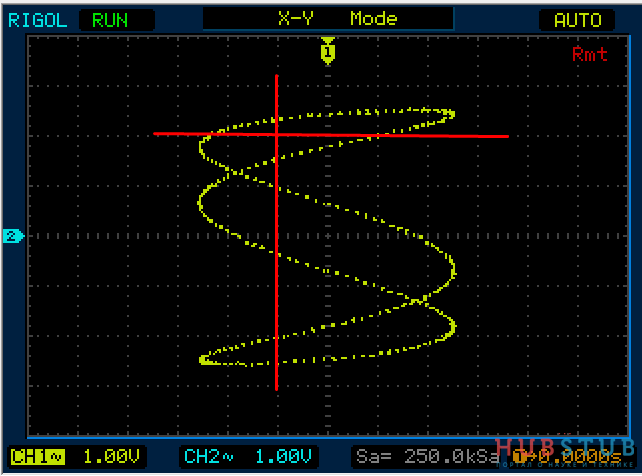
Для определения соотношения частот проведём горизонтальную и вертикальную прямые, пересекающие фигуру. При этом через точки пересечения линий самой фигуры эти прямые проходить не должны.
Тогда количество пересечений фигуры с горизонтальной прямой соответствует количеству изменений напряжения одного сигнала, а с вертикальной – количеству изменений напряжения другого сигнала. А из соотношения количества изменений сигналов можно найти соотношение частот колебаний.
А теперь тоже самое простыми словами, если синус с частотой 10KHz два раза пересекает горизонтальную прямую, а синус с неизвестной нам частотой пересекает четыре раза вертикальную прямую, то ясно что их частоты относятся как один к двум и частота неизвестного сигнала в два раза больше, то есть 20KHz. Кстати на осциллограмме выше частоты относятся как 6/4 или 3/2.
Почему мы один раз считаем пересечения с горизонтальной прямой, а второй с вертикальной?
Ответ на этот вопрос можно найти в определении фигуры Лиссажу:
Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу.
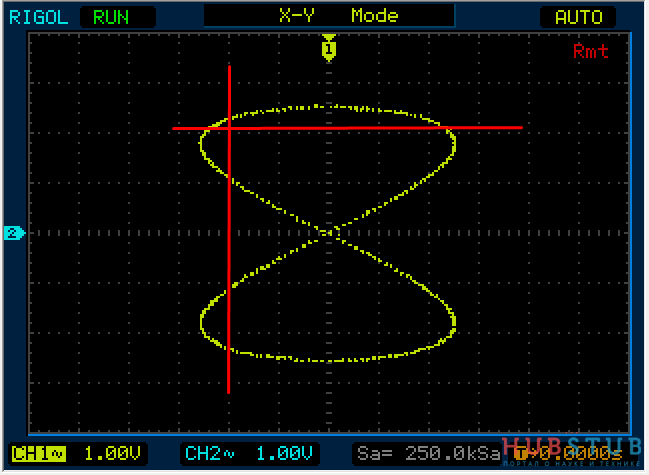
Давайте на подадим на оба входа осциллографа синус с частотой 1KHz и посмотрим как будут выглядеть фигура Лиссажу в зависимости от разности фаз между каналами.
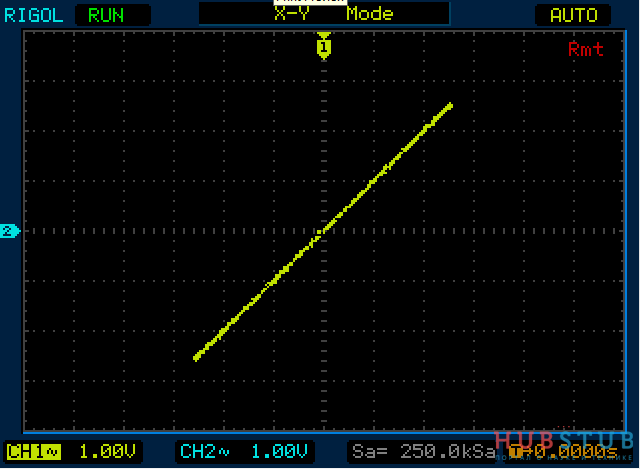
Разность фаз равна 0 °.
На осциллограммах видно, что количество пересечений с вертикальной и горизонтальной прямой одинаковое.
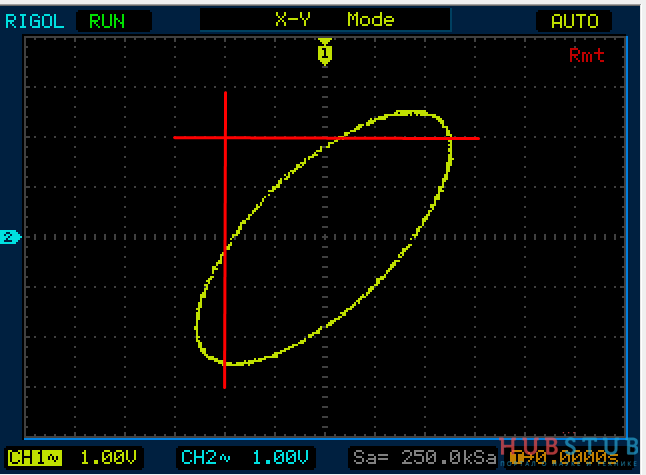
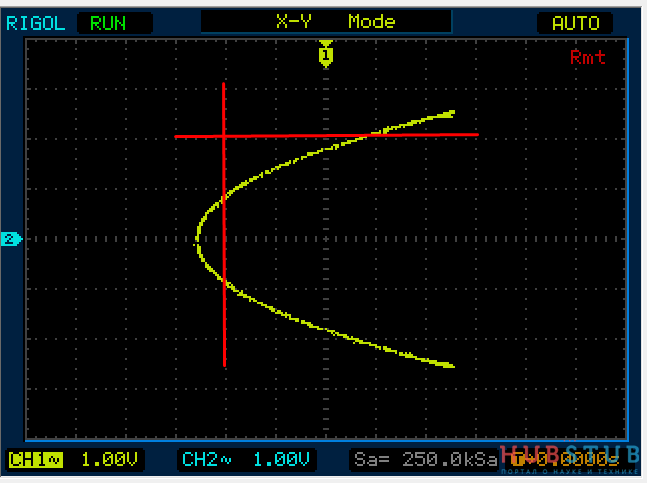
Теперь проделаем тоже самое но для частот 1KHz и 2KHz.
Разность фаз равна 0 °.
На осциллограммах видно, что количество пересечений с вертикальной прямой в два раза больше чем с горизонтальной.
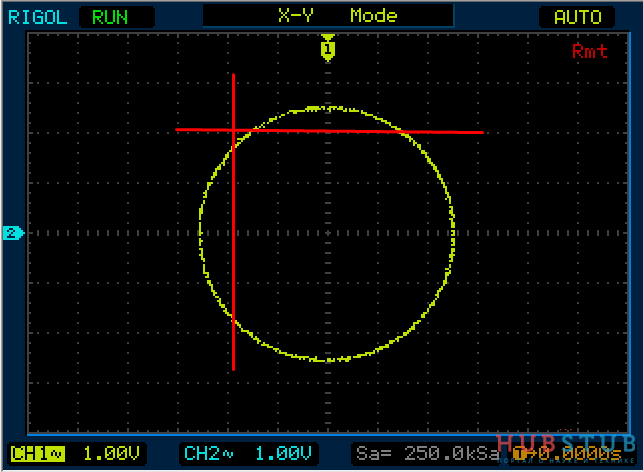
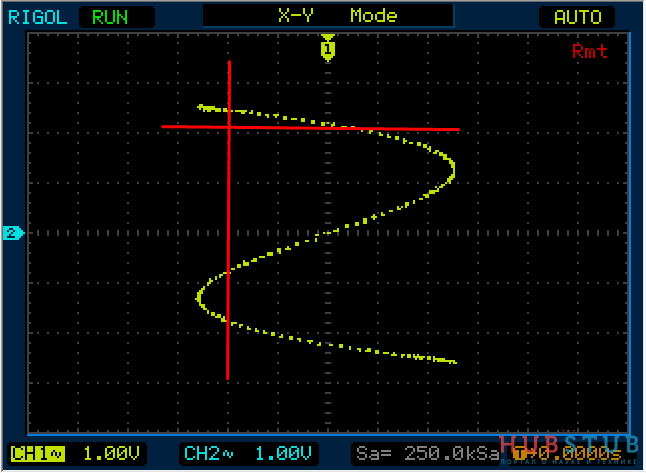
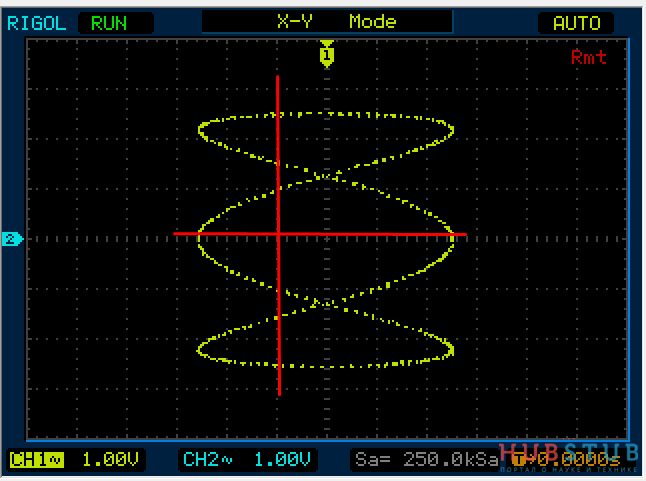
Теперь на один вход подадим 1Khz, а на второй 3Khz и проделаем тоже самое.
Разность фаз равна 0 °.
На осциллограммах видно, что количество пересечений с вертикальной прямой в три раза больше чем с горизонтальной.
Оказывается определить частоту неизвестного сигнала очень просто, если знать это замечательно свойство фигур Лиссажу.
Источник
Фигуры Лиссажу
Что такое фигуры Лиссажу?
Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.
Чтобы было более понятно, давайте представим девочку на качели из покрышки:
И вот представьте, что сзади ее раскачивает папа, а сбоку — мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится — это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.
Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:
1 — это горизонтальные пластины
2 — вертикальные пластины
ну и остальные детали — это составляющие электронной пушки.
Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные — другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.
Как получить фигуры Лиссажу
Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.
и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON
Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.
Режим XY-осциллографа
Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y — напряжение. Поэтому, по умолчанию, мы на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.
А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади — папа? Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.
Строим фигуры Лиссажу на осциллографе
Цепляем на один канал один генератор частоты, а на другой канал — другой генератор частоты:
На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:
Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display
Ну а потом с помощью дисплейных клавиш выбираем режим XY
И получается примерно вот такая хаотическая картинка:
Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.
А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:
Если взять 100 Герц на первом генераторе и на втором генераторе, то получим что-то типа этого:
В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой — через фазовращатель.
Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:
Эта фигура тоже все время крутится на осциллографе.
Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 😉
Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:
Вот такие фигуры вы будете видеть на экране своего осциллографа:
А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов


А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:

В основном фигуры Лиссажу в электронике можно использовать тогда, когда надо узнать частоту неизвестного генератора через образцовый генератор, частоту которого мы знаем, а также узнать сдвиг фаз между двумя одинаковыми сигналами. Ну и второе применение — это чисто визуальный кайф при вращении этих фигур на экранчике вашего осциллографа 😉
Источник
LabsMech&MolPhys / 121
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Техническая физика»
Лаборатория механики и молекулярной физики
Лабораторная работа №121
СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Составители: Гуща Е.Л., Шеденков С.И., Степанов М.А.
1. Изучить теоретический материал по сложению гармонических колебаний.
2. Экспериментально получить фигуры Лиссажу при сложении электромагнитных колебаний.
3. Определить отношение частот колебаний двойного физического маятника.
1. Т.И.Трофимова. Курс физики.– М.: Высшая школа, 1985. с.209-212.
2. И.В.Савельев. Курс физики. – М.: Высшая школа, 1989. с.238-296, 256-269.
Порядок теоретической подготовки к выполнению работы
Разобрать и законспектировать в рабочую тетрадь ответы на контрольные вопросы.
1. Что называется колебанием? Дайте определение свободных и вынужденных колебаний, автоколебаний.
2. Какие колебания называют гармоническими?
3. Дайте определение следующих величин: амплитуда, период, частота, круговая (циклическая) частота, фаза, начальная фаза колебаний.
4. Как изображаются гармонические колебания методом векторных диаграмм?
5. Сформулируйте условия, при которых при сложении двух колебаний одного направления и одинаковой частоты амплитуда результирующего колебания имеет максимальное и минимальное значения.
6. Какие колебания называются биениями?
7. Что называется периодом биений и от чего он зависит?
8. Что называется фигурой Лиссажу?
9. Способы определения отношения частот складываемых колебаний по фигурам Лиссажу.
Приборы и принадлежности
Стенд с двойным физическим маятником и блоком питания на 5 кВ Генератор высокочастотных сигналов Осциллограф Понижающий трансформатор
Указания по технике безопасности
Приборы питаются от сети переменного тока напряжением 220 В. Не разрешается работать
при поврежденной изоляции соединительных проводов.
Напряжение в 220 В в блоке питания двойного физического маятника преобразуется в 5000
В. Категорически запрещается включать стенд с маятником при открытой дверце
Отчет по лабораторной работе должен содержать
2) перечень приборов и принадлежностей к работе;
3) схему лабораторной установки;
4) физическую модель;
6) таблицу с рисунками фигур Лиссажу;
7) лист-вкладыш с фигурой Лиссажу, прочерченной двойным физическим маятником;
Теоретическое введение
1.1. Гармонические колебания.
Колебаниями называются движения или процессы, повторяющиеся во времени. Колебания широко распространены в природе и технике. Повторяемостью обладают,
например, качания маятника часов, колебания струны, напряжение между обкладками конденсатора в колебательном контуре радиоприемника и т.п.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания.
Свободными или собственными называются такие колебания, которые совершаются без внешних воздействий за счет первоначально полученной системой энергии.
Вынужденными называются такие колебания, которые возникают в системе под действием внешней периодически изменяющейся силы.
Автоколебания , как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешней периодической силы, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой.
Колебания, при которых величины, характеризующие колебательный процесс, изменяются со временем по закону синуса или косинуса, называются гармоническими . Все колебания в природе и технике или имеют характер очень близкий к гармоническим колебаниям, или их можно представить как наложение нескольких гармонических колебаний.
В случае гармонических колебаний изменение со временем колеблющейся величины x описывается формулой
x = A cos( ω t + ϕ 0 ) .
График гармонического колебания показан на рис.1. Величина x характеризует отклонение колеблющейся системы от положения равновесия ( x = 0) в любой момент времени t . Наибольшее значение колеблющейся величины x называется амплитудой колебаний A . Величина ( ω t + ϕ 0 ) , стоящая под знаком косинуса, называется фазой колебаний. Она
определяет состояние системы, т.е. положение и направление движения колеблющегося тела в данный момент времени.
Постоянная величина φ 0 представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебаний. Начальная фаза определяет значение x в начальный момент времени. Для колебания, изображенного на рис.1, начальная фаза равна φ 0 = 0.
Рис. 1. График гармонического колебания.
Периодом колебаний Т называется наименьший промежуток времени, по истечении которого состояние колеблющейся системы повторяется (совершается одно полное колебание) и фаза колебания получает приращение 2 π :
Источник