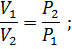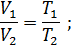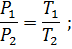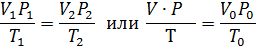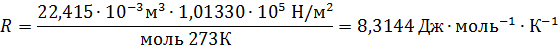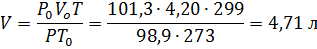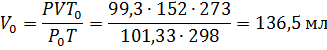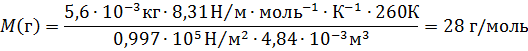Способы определения молярной массы газов
Существует ряд методов определения молекулярной массы газов при определенных внешних параметрах: давлении (Р), объеме (V) и температуре (Т).
1. По закону Авогадро и следствиям из него
Закон Авогадро: в равных объемах различных газов при одинаковых температуре и давлении содержится одинаковое число молекул.
Следствие 1: один моль любого вещества содержит количество структурных единиц данного вещества, равное постоянной Авогадро (Na = 6,02∙10 23 моль -1 ).
Следствие 2: при нормальных условиях (н.у.) (Р = 10 5 Па, Т = 273 К) один моль любого газа занимает объем 22,4 л. Эта величина получила название молярный объем (VM).
Зная массу m (г) какого-либо объема газа при н.у. и его объем V0 (л), можно рассчитать его молекулярную массу.
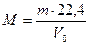 . . | (2.3.1) |
Следствие 3: массы равных объемов двух газов, взятых при одинаковых давлении и температуре, относятся друг к другу, как их молярные массы:
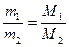 . . | (2.3.2) |
Отношение массы определенного объема первого газа к массе такого же объема второго газа (взятого при тех же условиях) называется относительной плотностью первого газа по второму (D). Тогда:
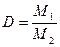 . . | (2.3.3) |
Обычно плотность газа определяют по отношению к водороду (DH2) или воздуху ( 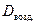
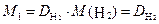 · 2, · 2, | (2.3.4) |
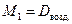 М возд.= М возд.= 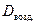 ·29. ·29. | (2.3.5) |
С учётом вышеуказанных условий для расчёта количества вещества используют следующие соотношения:
n 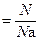 , , | (2.3.6) |
где N – количество структурных единиц в системе;
n 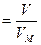 , , | (2.3.7) |
2. По уравнению Клапейрона – Менделеева
Если условия, в которых находится газ, отличны от нормальных, то параметры газа определяют по уравнению Клапейрона – Менделеева:
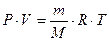 , , | (2.3.8) |
тогда молекулярную массу газа рассчитывают по формуле: 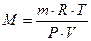 . . | (2.3.9) |
Единицы измерения величин в данном уравнении зависят от того, в каких единицах выражена масса (табл.1.2.1).
Источник
Законы газового состояния. Определение молярных масс газообразных веществ



Три параметра – объем V, давление P и температура T (T=273+t) – определяют физическое состояние газа. Давление 1,013∙10 5 Па (760 мм рт. ст.) и температура 273 К или 0 о С называют нормальными условиями состояния газа, что в буквенных обозначениях этих величин указывается индексом: Po, To, to. Объем газа при н.у. – Vo.
Закон Бойля – Мариотта. При постоянной температуре объем данной массы газа изменяется обратно пропорционально давлению:
Закон Гей-Люссака. При постоянном давлении объем данной массы газа меняется прямо пропорционально абсолютной температуре
При постоянном объеме:
Уравнение Менделеева – Клапейрона. Объединение законов Бойля, Мариотта и Гей-Люссака дает уравнение состояния газа
если одно из состояний является нормальным. Для любого газа количеством вещества 1 моль величина 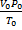
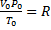
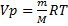
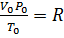
Если объем газа измерен в литрах, а давление газа в мегапаскалях (МПа=10 6 Па), то R=0,083л∙МПа∙моль -1 ∙К -1 . В расчетах обычно используют числа, имеющие три значащие цифры, что дает вполне достаточную точность: 22,4910 -3 м 3 , 22,4 л, 273 К, 8,31 Дж∙моль -1 ∙К -1 .
Согласно закону Авогадро, в равных объемах любых газов, взятых при одной и той же температуре и одинаковом давлении, содержится одинаковое число молекул.
Иными словами, одно и то же число молекул любого газа занимает при одинаковых условиях один и тот же объем. Вместе с тем 1 моль любого газа содержит одинаковое число молекул. Следовательно, при одинаковых условиях 1 моль любого газа занимает один и тот же объем. Этот объем называется мольным объемом газа и при нормальных условиях (0 0 С, давление 101,325 кПа) равен 22,4 л.
Пример 1.Определить объём, занимаемый 5,25 г азота при 26 0 С и давлении 98,9 кПа (742 мм рт.ст.).
Решение. Зная мольный объём и мольную массу (28,0 г/моль) азота, находим объём, который будут занимать 5,25 г азота при нормальных условиях:
28,0 г азота занимают объём 22,4л
5,25 г азота занимают объём VO ,
откуда VO = 5,25∙22,4/ 28,0 = 4,20 л
Затем приводим полученный объём к указанным в задаче условиям:
Пример 2.При25 0 С и давлении 99,3 кПа (745 мм рт.ст.) некоторое количество газа занимает объём 152 мл. Найти, какой объём займет это же количество газа при 0 0 С и давлении101,33 кПа.
Решение. Подставляя данные задачи в последнее уравнение, получаем:
Пример 3.Некоторый газ массой 5,6 г занимает объём 4,84 л притемпературе 17 0 С и давлении 0,997∙10 5 Па. Чему равна относительная молекулярная масса этого газа?
Решение. Из уравнения Менделеева-Клайперона 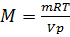
Так как числовое значение молярной массы, выраженной в г/моль, равно относительной молекулярной массе, т.е.
Источник
Способы определения молярной массы газообразных веществ
По закону Авогадро равные объемы газов, взятые при одинаковой температуре и одинаковом давлении, содержат равное число молекул. Отсюда следует, что массы двух газов, взятых в одинаковых объемах, должны относиться друг к другу, как их молекулярные массы или как численно равные их молярные массы:
Здесь 



Отношение массы данного газа к массе другого газа, взятого в том же объеме, при той же температуре и том же давлении, называется относительной плотностью первого газа по второму.
Например, при нормальных условиях масса диоксида углерода в объеме 1 л равна 1,98 грамм, а масса водорода в том же объеме и при тех же условиях — 0,09 грамм, откуда плотность диоксида углерода по водороду составит:
Обозначим относительную плотность газа 
Молярная масса газа равна его плотности по отношению к другому газу, умноженной на молярную массу второго газа.
Часто плотности различных газов определяют по отношению к водороду, как самому легкому из всех газов. Поскольку молярная масса водорода равна 2,0158 г/моль, то в этом случае уравнение для расчета молярных масс принимает вид
или, если округлить молярную массу водорода до 2:
Вычисляя, например, по этому уравнению молярную массу диоксида углерода, плотность которого по водороду, как указано выше, равна 22, находим:
Нередко также молярную массу газа вычисляют, исходя из его плотности по воздуху. Хотя воздух представляет собой смесь нескольких газов, все же можно говорить о средней молярной массе воздуха, определенной из плотности воздуха по водороду. Найденная таким путем молярная масса воздуха равна 29 г/моль.
Обозначив плотность исследуемого газа по воздуху через 
Молярную массу вещества (а следовательно, и его относительную молекулярную массу) можно определить и другим способом, используя понятие о молярном объеме вещества в газообразном состоянии. Для этого находят объем, занимаемый при нормальных условиях определенной массой данного вещества в газообразном состоянии, а затем вычисляют массу 
Пример. 0,7924 грамм хлора при 

Находим массу хлора, содержащегося в объеме 
Следовательно, молярная масса хлора равна 71 г/моль, а относительная молекулярная масса хлора равна 71.
Измерения объемов газов обычно проводят при условиях, отличных от нормальных. Для приведения объема газа к нормальным условиям можно пользоваться уравнением, объединяющим газовые законы Бойля — Мариотта и Гей-Люссака
Здесь V объем газа при давлении Р и температуре Т; 



Молярные массы газов можно вычислить также, пользуясь уравнением состояния идеального газа — уравнением Клапейрона — Менделеева
где Р — давление газа, 


Если объем газа выражен в литрах, то уравнение Клапейрона — Менделеева приобретает вид
Описанными способами можно определять молекулярные массы не только газов, но и всех веществ, переходящих при нагревании (без разложения) в газообразное состояние. Для этого навеску исследуемого вещества превращают в пар и измеряют его объем, температуру и давление. Последующие вычисления производят так же, как и при определении молекулярных масс газов.
Молекулярные массы, определенные этими способами, не вполне точны, потому что рассмотренные газовые законы и уравнение Клапейрона — Менделеева строго справедливы лишь при очень малых давлениях (см. § 11). Более точно молекулярные массы вычисляют на основании данных анализа вещества (см. § 14).
Источник