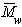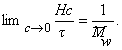Способы определения молекулярной массы полимеров

3.5. Молекулярные массы полимеров и методы их определения

Растворение полимеров является единственным способом их диспергирования до молекулярного уровня, благодаря чему становится возможным изучение характеристик индивидуальных макромолекул (размера, формы, молекулярной массы и т.д.).

Важнейшей особенностью полимеров являются большие значения их молекулярных масс (от нескольких тысяч до нескольких миллионов) и неидентичность их молекул, что обусловливает необычные и ценные свойства полимеров. В отличие от низкомолекулярных соединений полимеры представляют собой смесь макромолекул различной длины, т.е. они неоднородны по молекулярной массе. Существование в образце полимера макромолекул разной длины обусловлено многими причинами, и в первую очередь механизмом реакций их синтеза.

Разделение полимера на фракции более или менее однородные по молекулярной массе называется фракционированием. Ряд методов фракционирования основан на зависимости растворимости полимера от его молекулярной массы. Чем больше молекулярная масса, тем хуже растворимость полимера. Различают два типа фракционирования:препаративное, при котором выделяют фракции и изучают их свойства, и аналитическое, при котором получают кривую распределения без выделения отдельных фракций. Наиболее часто из препаративных методов используют методы фракционного осаждения и фракционного растворения.

Метод фракционного осаждения состоит в последовательном осаждении из раствора полимера ряда фракций, молекулярные массы которых монотонно убывают. Вызвать осаждение фракций можно различными способами;а) добавлением осадителя к раствору полимера; б) испарением растворителя, если полимер был предварительно растворён в смеси растворитель -осадитель; в) изменением температуры раствора, которое приводит к ухудшению качества растворителя.

Метод фракционного растворения состоит в последовательном экстрагировании полимера рядом жидкостей, растворяющая способность которых по отношению к данному полимеру последовательно возрастает. Получаемые фракции обладают последовательно возрастающими молекулярными массами. Путём раздельного изучения этих фракций, т.е. измерения их средних молекулярных масс, удаётся построить кривую распределения помолекулярной массе всего полимера в целом.

Значение молекулярной массы полимера является некоторой средней величиной по ансамблю макромолекул. Средняя молекулярная масса складывается из суммы произведений молекулярных масс каждого компонента |М₁, М₂, М₃ и т.д.) на его долю (а₁, а₂, а₃ ) в смеси полимергомологов:

Различают среднечисловую М_n и среднемассовую М_ω молекулярные массы. Физическое различие между ними сводится к характеруэксперимента, с помощью которого они измеряются, т.е. основан ли этот эксперимент на определении числа макромолекул (количества вещества) или на определении концентрации полимера г/дм 3 .

Среднечисловую молекулярную массу определяют делением массы образца полимера на число молекул:

где N₁ ,N₂ ,N_i – число макромолекул с молекулярными массами соответственно М₁ М₂ М_i.

Среднемассовую молекулярную массу определяют по формуле

где ω – массовая доля макромолекул с молекулярной массой М.

На значения среднечисловой молекулярной массы большее влияние оказывает содержание в полимере низкомолекулярных фракций, а на значение среднемассовой молекулярной массы — содержание высокомолекулярных фракций.

Среднечисловую молекулярную массу определяют по данным измерений, основанных на подсчёте числа молекул М, причём вклад каждоймолекулы одинаков и не зависит от её молекулярной массы.

Для определения молекулярной массы полимеров используют следующие методы.

1. химические методы основанные на определении функциональных групп (методконцевых групп).

2. термодинамические методы основанные на термодинамических свойвствах разбавленных растворов полимеров (измерение осмотического давления, криоскопия, эбуллиоскопия).

3. молекулярно-кинетические методы (измерение скорости диффузии), ультрацентрифугирование, измерение вязкости растворов полимеров.

4. оптические методы (основанные на измерении светорассеивания в растворах полимерах).

Наиболее часто используют метод концевых групп, осмометрический метод, метод ультрацентрифугирования, метод светорассеивания, вискозиметрический метод.

Метод концевых групп применяется для конденсационных линейных полимеров,которые содержат реакционно-способные функциональные концевые группы ОН, -СООН, NH₂ и др и позволяет определить молекулярную массуполимеров в пределах от 10 3 до 10 5 _. Среднечисловую молекулярную массу находят по уравнению

Где Z- число концевых групп на макромолекулу,E– молярная масса концевой группы,e– экспериментально найденное содержание концевых групп в %. Определить число концевых групп можно титриметрическими или колориметрическими методами.

Среднемассовая молекулярная масса определяется по данным измерений, основанных на определении массовой доли молекул с молекулярной массой М|. Для определения используют вискозиметрию, диффузионные методы, ультрацентрифугирование и метод светорассеяния.

Наиболее простым методом определения молекулярной массы является вискозиметрический метод.

Вискозиметрический метод основан на том, что линейные макромолекулы, находящиеся в растворителе, даже при относительно низких концентрациях значительно повышают его вязкость, причем повышение вязкости раствора пропорционально увеличению молекулярной массы. Этот метод применим только к линейным и мало разветвленным мапкромолекулам и не подходит для шарообразных или сильно разветвленных макромолекул.

Вязкость жидкостей определяют с помощью прибора, называемоговискозиметром. При исследовании разбавленных растворов полимеровопределяют обычно не абсолютную вязкость, а относительную, которая при условии, когда плотности разбавленного раствора и чистого растворителяпрактически совпадают, равна отношению, вязкости раствора полимера(η) квязкости чистого растворителя (η₀)

где t и t₀ — время истечения соответственно раствора и растворителя.

Определение времени истечения раствора и растворителя производятся при строго определённой температуре, так как вязкость зависит от температуры.

Исходя из относительной вязкости рассчитывают удельную (η _уд)и приведенную вязкость(η _пр).

где с – концентрация полимера г/100см 3 .

Удельная вязкостьпоказывает относительный прирост вязкостивследствие введения в растворитель полимера, а приведенная вязкость — это удельная вязкость, отнесённая к единице концентрации полимера (с). Приведенная вязкость линейно зависит отконцентрации раствора полимера. Экстраполяцией этой зависимости до нулевой концентрации определяют характеристическую вязкость [η] полимера:

[η] = lim η _уд /с при с→0.

Наиболее часто измерения характеристической вязкости используются для определения молекулярной массы вискозиметрическим способом.

Для большинства полимеров наблюдается зависимость характеристической вязкости от молекулярной массы полимера, выражаемая уравнением Марка-Хаувинка-Куна:

где К — постоянная константа, зависящая от температуры и природы полимера и растворителя;

α — показатель, характеризующий конформацию макромолекул в растворе, и зависит от всех факторов, влияющих на конформацию цепи.

Величина α в зависимости от природы растворителя может меняться от 0,5 для статистического молекулярного клубка до 2,0 для абсолютно жёсткой молекулы. Величина К изменяется в пределах от 10 -2 до 10 -5 и зависит от выбора системы полимер — растворитель. Значения К и α берутся из литературных данных.

Определив значение характеристической вязкости при известных величинах констант К α и вычисляют молекулярную массуполимера.

Для расчёта молекулярной массы подставляют значения [η], констант Ки α и логарифмируют уравнение Марка -Хаувинка — Куна

lg[ η] = lg К + α lg M

Характеристическая вязкость определяет поведение изолированныхмакромолекул. Она представляет собой меру потерь энергии на трениеизолированных макромолекул о растворитель при их поступательномдвижении с градиентом скорости отличным от нуля. Характеристическаявязкость зависит от размеров макромолекул в растворе, от природырастворителя и температуры. Поэтому характеристические вязкости имолекулярные массы для одного и того же полимера, измеренные в разныхрастворителях, отличаются, так как константы α различны (например, вхорошем и плохом растворителях).

Источник

Основные методы определения молекулярной массы

Осмометрический метод. Метод основан на измерении осмотического давления разбавлен­ных растворов полимеров.

Молекулярную массу определяют по величине измеренного давле­ния, пользуясь уравнением Вант-Гоффа в вириальной форме:

,

где p— осмотическое давление, атм;

С — массовая концентрация полимера, г/мл;

Т — абсолютная температура;

R— газовая постоянная;

Коэффициент A₂ характеризует взаимодействие между полимером и растворителем.

При бесконечном разбавлении уравнение принимает вид;

.

Предельное значение p/С при С 0 находят, измеряя осмоти­ческое давление ряда растворов полимера при малых концентрациях, путем графической экстраполяции зависимости p/С от С к нулевой концентрации.

Молекулярная масса, определяемый осмометрическим методом, является среднечисловым.

Метод светорассеяния.Измерение рассеяния света растворами полимеров — один из важнейших методов определения среднемассовой молекулярной массы полимеров в интервале . Широкое применение получил метод Дебая, при котором используют визуальный нефело­метр, предназначенный для измерения интенсивности рассеянного света раствором под углом 90° и асимметрии светорассеяния под углами 45 и 135° к падающему световому пучку *.

Для определения молекулярной массы необходимо измерить вели­чину , называемую приведенной интенсивностью рассеяния и про­порциональную отношению интенсивности света , рассеянногоединицей объема среды под углом , к интенсивности падающего светового пучка .

При и бесконечном разведении

Таким образом, для определения молекулярной маассы полимера необходимо измерить под углом 90° приведенные интенсивности рассеяния раствора при различных концентрациях и раство­рителя .

Построив график зависимости КС/ от С, экстраполяцией полученной прямой к нулевой концентрации находят обратную величину молекулярной массы полимера 1/М.

Вискозиметрический метод. Вискозиметрический метод — наиболее простой и доступный метод определения молекулярной массы полимеров в широкой области значений молекулярных масс. Этот метод является косвенным и требует определения констант в уравнении, выражающем зави­симость вязкости от молекулярных масс.

Для определения вязкости раствора полимера измеряют время истечения t₀ и t (в сек),равных объемов растворителя и раствора через капилляр вискозиметра при заданной постоянной температуре. Концентрацию раствора (С)обычно выражают в граммах на 100 мл растворителя; для измерения вязкости используют растворы с С

Контрольные вопросы

1.1.Что такое полидисперсность? Назовите монодисперсные и полидисперсные полимеры.

2.Какие методы усреднения молекулярных масс полимеров знаете?

3.3.Для чего необходимо знать молекулярно-массовые распределение полимеров (ММР)?

4.Принцип построения интегрального и дифференциального кривых ММР.

5.Какие методы фракционирования знаете?

6.В чем суть вискозиметрического метода определения молекулярной массы полимеров?

7.Для чего применяется гель-проникающая хроматография?

8.Принцип определения молекулярной массы полимеров методом светорассеяния.

9.Какими методами определяют среднечисловую молекулярную массу. Опишите осмометрический метод.

Источник

5.2.2. Методы определения молекулярной массы полимеров по свойствам растворов
Свойства растворов

Наиболее часто среднечисленную молекулярную массу 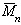полимеров находят методом осмотического давления, который основан на изучении явления осмоса — одностороннего проникновения молекул растворителя через полупроницаемую мембрану, не пропускающую молекулы полимера. Количественной характеристикой явления осмоса служит осмотическое давление, пропорциональное числу молекул в единице объёма раствора.

Молекулярная масса определяется как коэффициент, связывающий весовую и частичную концентрации

, (2.5.12)

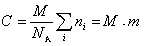
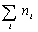
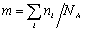
где С – весовая концентрация, г/см 3 ; — суммарная частичная концентрация, молекул/см 3 ; — мольная концентрация, моль/см 3 .

Таким образом, задача сводится к определению мольной концентрации раствора известной весовой концентрации.

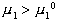
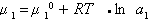
Стремление молекул растворителя к самопроизвольному проникновению через мембрану определяется разностью химических потенциалов растворителя в частях системы, разделенных перегородкой, причем , так как из химической термодинамики известно, что для растворов

,

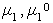
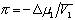
где — химический потенциал раствора при активности раствора aи стандартный химический потенциал.

, (2.5.13)

где 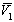– парциальный мольный объём растворителя, p — служит количественной мерой сродства между компонентами раствора.

Связь между осмотическим давлением и весовой концентрацией растворов описывается следующими уравнениями:

(уравнение Вант-Гоффа) для растворов низкомолекулярных веществ

, (2.5.14)

, (2.5.15)

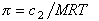
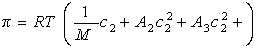
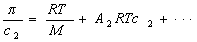
где А₂ – второй вириальный коэффициент, характеризующий взаимодействие полимера с растворителем и форму макромолекул в растворе, обычно А₃®0.

Величина p /c₂ носит название приведенного осмотического давления. На рис. 2.50 показан пример зависимости приведенного осмотического давления для растворов полимера в различных растворителях. Чем больше наклон прямых, тем сильнее проявляется взаимодействие между компонентами раствора и тем больше величина

, (2.5.16)

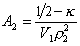
где k- параметр взаимодействия, r₂ – плотность полимера в растворе, V₁ – мольный объём растворителя.

При k = 0,5 А₂ =0 и раствор ведет себя как идеальный. Таким образом, определяя наклон зависимости p /c₂ = fc_{2 ,} можно охарактеризовать сродство компонентов раствора. Величина молекулярной массы определяется как

. (2.5.17)

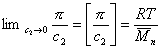
Найденная из измерений осмотического давления молекулярная масса характеризует .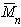

Метод светорассеяния. Среднемассовая молекулярная масса

Явление светорассеяния в растворах полимеров наблюдается в том случае, если размер макромолекул менее l/2 — половины длины волны проходящего света. Существуют различные теории рассеяния света, положенные в основу расчетных уравнений экспериментальных методов определения молекулярной массы. При условии, что размер молекул полимера меньше l/2, для растворов полимеров справедлива теория рассеяния света Эйнштейна.

Если рассеяние света происходит на сферических частицах, то интенсивность рассеяния будет одинаковой во всех направлениях. Обозначим угол, под которым по отношению к падающему лучу определяется интенсивность рассеянного света, Q. Рассеивающая способность характеризуется коэффициентом рассеяния R:

(2.5.18)

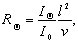
где I_Q, I₀— интенсивность рассеянного и падающего света; l– расстояние, на котором наблюдается рассеянный свет от рассеивающего объёма; v – рассеивающий объём.

В практике определения интенсивности рассеянного света наиболее часто определяется R₉₀, т.е. рассеяние света под углом 90 o , хотя с помощью современных приборов, особенно использующих в качестве источника света лазер, можно определять интенсивность рассеянного света от Q = 4 o .

Для расчета молекулярной массы полимеров используется уравнение Дебая:

, (2.5.19)

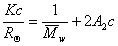
где с – весовая концентрация, г/см 3 ; K – оптическая постоянная, зависящая от коэффициента преломления среды (n₀), концентрационного инкремента коэффициента преломления раствора (dn/dc) и длины волны света l,

. (2.5.20)

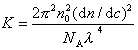
Таким образом для определения молекулярной массы следует измерять угловое рассеяние света, коэффициент преломления среды. Особенно тщательно следует определять (dn/dc), так как эта величина обычно чрезвычайно мала. Следует привлекать приборы, позволяющие определить коэффициент преломления с точностью до 6-го знака.

По аналогии с поглощением света можем записать для интенсивности рассеяния

(2.5.21)

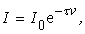
гдеt – мутность 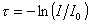при v =1; I – интенсивность света, прошедшего через раствор после рассеяния.

Мутность связана с коэффициентом рассеяния соотношением

(2.5.22)

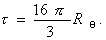
Поэтому, с учетом уравнения (2.5.19), можно проводить расчет молекулярной массы по уравнению

, (2.5.23)

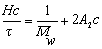
где Н – оптическая постоянная, Н = 16p K/3.

Для расчета молекулярной массы определяется величина

По углу наклона можно определить значение А₂ и охарактеризовать взаимодействие компонентов раствора. Изменение температуры, замена растворителя могут вызвать изменение межмолекулярного взаимодействия компонентов раствора и формы макромолекул в растворе.

Молекулы могут приобретать и асимметрическую форму. В этом случае рассеяние света под разными углами к падающему лучу будет неравномерным и найденное значение молекулярной массы содержит погрешность. Поэтому необходимо вводить поправку на внутреннюю интерференцию света, появляющуюся в результате рассеяния света с некоторой разностью фаз от различных участков молекул. Для введения поправок существуют два основных метода: метод Дебая и метод Зимма.

Метод Дебая основан на измерении интенсивности рассеянного света при значении углов рассеяния, равных 135 и 45 o , соответственно R₄₅ и R₁₃₅. Отношение интенсивности равно отношению поправок Р и называется коэффициентом асимметрии

Величина z зависит от концентрации раствора, так как форма макромолекул в растворе может изменяться с увеличением концентрации. Для определения истинного значения z строят зависимость 1/(z-1)=fс и определяют 1/([z]-1) = lim_с®0 1/(z-1).

Зная z,по существующим таблицам находят величину Р, которую вводят в расчетное уравнение

. (2.5.25)

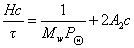
Метод Зимма основан на построении специальной диаграммы, на которой по оси абсцисс откладывается и концентрация, и угол рассеяния света. Линии на диаграмме образуют два семейства параллельных (практически прямых) линий. Более крутые линии представляют собой зависимость рассеяния света от концентрации растворов. Более пологие – зависимость рассеяния света от угла определения. Нижняя линия соответствует рассеянию света при с = 0, крайняя левая — дает совокупность точек при sin Q/2 =0. Обе прямые пересекаются с осью ординат в точке, характеризующей 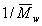. Этот метод более точный, чем метод Дебая и позволяет рассчитать молекулярную массу полимера, не определяя и не постулируя форму макромолекул в растворе.

Для определения молекулярной массы полимеров можно измерять коэффициент диффузии растворенного вещества. Если представить, что макромолекулы имеют узкое распределение по молекулярной массе и каждая молекула не взаимодействует с другими молекулами полимера, то для молекулы, перемещающейся вдали от стенки сосуда, сила трения со средой может быть описана выражением

, (2.5.26)

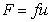
где F- сила трения; u – скорость перемещения молекулы; f =6ph₀r- коэффициент трения сферических частиц; h₀ – вязкость растворителя; r – радиус макромолекулы в растворе.

Уравнение (2.5.26) справедливо при скорости перемещения макромолекул 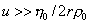, гдеr₀ – плотность растворителя.

Предполагая применимость уравнения Эйнштейна для диффузии полимерных молекул в растворе, запишем

. (2.5.27)

. (2.5.28)

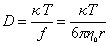
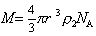
Сочетание (2.5.27) и (2.5.28) дает

. (2.5.29)

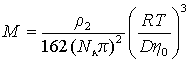
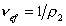
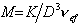
Cущественную ошибку может внести в расчет использование в качестве r₂ значения плотности полимера, так как в растворе плотность макромолекул может значительно отличаться от плотности “сухого” полимера. Поэтому следует использовать значение , которое можно определить из измерений вязкости.

, (2.5.30)

где v_ef— это тот удельный объём, который занимают макромолекулы в растворе, см 3 /г, учитывающий взаимодействие макромолекул в растворителе.

Вискозиметрический метод определенияv_ef и .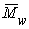

Существуют несколько уравнений, связывающих вязкость растворов полимеров с их концентрацией. Уравнение Симха для сферических частиц связывает удельную вязкость с объёмной концентрацией полимера:

, (2.5.31)

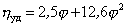
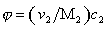
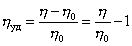
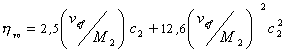
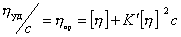
где j – объёмная доля, занимаемая полимером, ; c₂— массовая концентрация (г/см 3 ); v_ef— эффективный объём одного моля полимера.

,

. (2.5.32)

, (2.5.33)

где – характеристическая вязкость, a- коэффициент Эйнштейна формы макромолекул в растворе.

Уравнение (2.5.33) носит название уравнения Хаггинса, K’ – постоянная Хаггинса, характеризующая форму макромолекул в растворе. Для сферических макромолекул K’ = 2, для эллипсоид-

ных K’ = 2¸10; для игольчатых форм K’ 2 x – ускорение центробежного поля, w – угловая скорость вращения; x – расстояние от молекулы до центра вращения; m_h – масса одной сольватированной молекулы; v_h – объем одной молекулы, r₀ — плотность растворителя, v_hr₀ – поправка на выталкивающую силу.

Масса одной сольватированной молекулы, в соответствии с концепцией сольватированной частицы Онслея, определяется как

, (2.5.36)

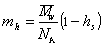
Объем одной сольватированной макромолекулы

, (2.5.37)

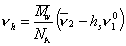
где v₂— парциальный удельный объем макромолекул, см 3 /г; h_sv₁ 0 — поправка на объем связанного растворителя; v₁ 0 = 1/r₀ – — удельный объем растворителя, см 3 /г.

С учетом (2.5.36) и (2.5.37) запишем уравнение (2.5.35) в виде

. (2.5.38)

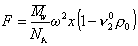
Можно видеть, что величина сольватации h_s исключается из расчетного уравнения. Сила трения, уравновешивающая центробежную силу в стационарном режиме,

. (2.5.39)

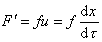
Из условия стационарности F= F’, следовательно,

. (2.5.40)

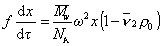
Для перехода от дифференциальной формы уравнения к интегральной Сведберг предложил использовать понятие постоянной седиментации

, (2.5.41)

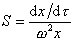
характеризующей скорость осаждения макромолекул под действием единицы центробежного поля. Эта постоянная зависит только от свойств макромолекул.

Коэффициент трения может быть определен из измерения коэффициента диффузии по уравнению Эйнштейна

,

. (2.5.42)

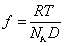
Уравнение (2.5.42) носит название уравнения Сведберга. Коэффициент диффузии D и коэффициент седиментации s определяются независимо. Для исключения эффекта взаимодействия макромолекул значение s экстраполируют к бесконечно малой концентрации и в расчетах используют значение s₀.

Метод седиментации позволяет наиболее точно определить значение молекулярной массы полимера, так как здесь не надо определять или предполагать форму макромолекул, а величина сольватации исключается из расчетного уравнения. Экспериментально установлено, что

. (2.5.43)

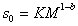
гдеK и b – постоянные, для многих полимеров приведенные в таблицах. Поэтому после калибровки постоянных уравнение (2.5.43) можно использовать для определения молекулярной массы без привлечения диффузионных измерений.

Определение средней молекулярной массы методом

По этому методу не проводят осаждения полимера, а ведут процесс только до установления равновесия между седиментацией и диффузией.

Для седиментационного потока

. (2.5.44)

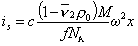
Для диффузионного потока

. (2.5.45)

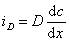
При седиментационно-диффузионном равновесии i_D= i_s, следовательно,

. (2.5.46)

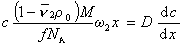
После преобразования с учетом D = kT/f и kN_А=R получаем

. (2.5.47)

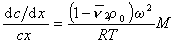
Откуда после интегрирования

. (2.5.48)

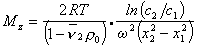
Таким образом достаточно определить значения концентрации раствора в двух точках кюветы чтобы рассчитать значение M_z . Этот метод носит название метода Арчибальда. Можно проводить расчет и по неустановившемуся равновесию, что значительно сокращает время эксперимента, но усложняет расчет.

Кроме определения молекулярной массы метод седиментационного ультрацентрифугирования в сочетании с вискозиметрией позволяет охарактеризовать форму макромолекул в растворе, определяя фактор Шераги — Манделькерна b, который для сферических частиц равен b = 2,12×10 6 .

Расчет проводится по формуле

, (2.5.49)

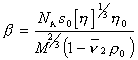
где s₀ – коэффициент седиментации, экстраполированный к бесконечному разбавлению; [h] – характеристическая вязкость;h₀ – вязкость растворителя.

Источник