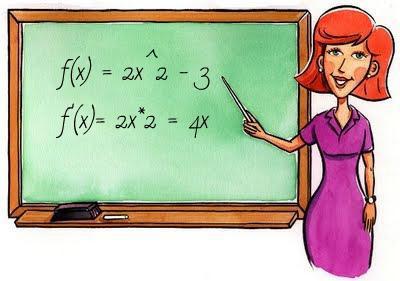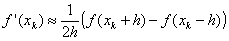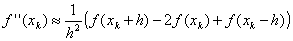Способы определения минимума функции

Как найти точки минимума и максимума функции: особенности, способы и примеры

Функция и исследование ее особенностей занимает одно из ключевых глав в современной математике. Главная составляющая любой функции — это графики, изображающие не только ее свойства, но также и параметры производной данной функции. Давайте разберемся в этой непростой теме. Итак, как лучше искать точки максимума и минимума функции?

Функция: определение

Любая переменная, которая каким-то образом зависит от значений другой величины, может называться функцией. Например, функция f(x 2 ) является квадратичной и определяет значения для всего множества х. Допустим, что х = 9, тогда значение нашей функции будет равно 9 2 = 81.

Функции бывают самых разных видов: логические, векторные, логарифмические, тригонометрические, числовые и другие. Их изучением занимались такие выдающиеся умы, как Лакруа, Лагранж, Лейбниц и Бернулли. Их труды служат оплотом в современных способах изучения функций. Перед тем как найти точки минимума, очень важно понять сам смысл функции и ее производной.

Производная и ее роль

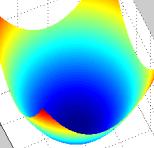
Все функции находятся в зависимости от их переменных величин, а это значит, что они могут в любой момент изменить свое значение. На графике это будет изображаться как кривая, которая то опускается, то поднимается по оси ординат (это все множество чисел «y» по вертикали графика). Так вот определение точки максимума и минимума функции как раз связано с этими «колебаниями». Объясним, в чем эта взаимосвязь.

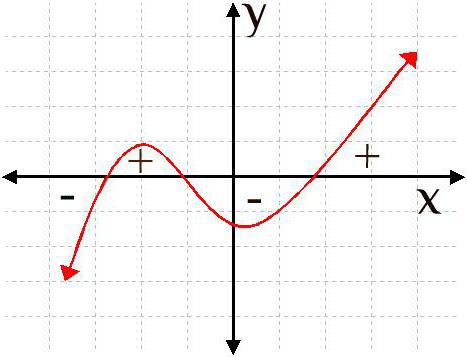
Производная любой функции изображается на графике с целью изучить ее основные характеристики и вычислить, как быстро изменяется функция (т.е. меняет свое значение в зависимости от переменной «x»). В тот момент, когда функция увеличивается, график ее производной будет также возрастать, но в любую секунду функция может начать уменьшаться, и тогда график производной будет убывать. Те точки, в которых производная переходит со знака минуса на плюс, называются точками минимума. Для того чтобы знать, как найти точки минимума, следует лучше разобраться с понятием производной.

Как вычислять производную?

Определение и вычисление производной функции подразумевает под собой несколько понятий из дифференциального исчисления. Вообще, само определение производной можно выразить следующим образом: это та величина, которая показывает скорость изменения функции.

Математический способ ее определения для многих учеников кажется сложным, однако на самом деле все гораздо проще. Необходимо лишь следовать стандартному плану нахождения производной любой функции. Ниже описано, как можно найти точку минимума функции, не применяя правила дифференцирования и не заучивая таблицу производных.

1. Вычислить производную функции можно с помощью графика. Для этого необходимо изобразить саму функцию, затем взять на ней одну точку (точка А на рис.) Вертикально вниз провести линию к оси абсцисс (точка х₀), а в точке А провести касательную к графику функции. Ось абсцисс и касательная образуют некий угол а. Для вычисления значения того, насколько быстро возрастает функция, необходимо вычислить тангенс этого угла а.
2. Получается, что тангенс угла между касательной и направлением оси х является производной функции на маленьком участке с точкой А. Данный метод считается геометрическим способом определения производной.

Способы исследования функции

В школьной программе математики возможно нахождение точки минимума функции двумя способами. Первый метод с помощью графика мы уже разобрали, а как же определить численное значение производной? Для этого потребуется выучить несколько формул, которые описывают свойства производной и помогают преобразовать переменные величины типа «х» в числа. Следующий метод является универсальным, поэтому его можно применять практически ко всем видам функций (как к геометрическим, так и логарифмическим).

1. Необходимо приравнять функцию к функции производной, а затем упростить выражение, используя правила дифференцирования.
2. В некоторых случаях, когда дана функция, в которой переменная «х» стоит в делителе, необходимо определить область допустимых значений, исключив из нее точку «0» (по простой причине того, что в математике ни в коем случае нельзя делить на ноль).
3. После этого следует преобразовать изначальный вид функции в простое уравнение, приравняв все выражение к нулю. Например, если функция выглядела так: f(x) = 2x 3 +38x, то по правилам дифференцирования ее производная равна f'(x) = 3x 2 +1. Тогда преобразуем это выражение в уравнение следующего вида: 3x 2 +1 = 0.
4. После решения уравнения и нахождения точек «х», следует изобразить их на оси абсцисс и определить, является ли производная в этих участках между отмеченными точками положительной или отрицательной. После обозначения станет ясно, в какой точке функция начинает убывать, то есть меняет знак с минуса на противоположный. Именно таким способом можно найти как точки минимума, так и максимума.

Правила дифференцирования

Самая основная составляющая в изучении функции и ее производной — это знание правил дифференцирования. Только с их помощью можно преобразовывать громоздкие выражения и большие сложные функции. Давайте ознакомимся с ними, их достаточно много, но все они весьма просты благодаря закономерным свойствам как степенных, так и логарифмических функций.

1. Производная любой константы равна нулю (f(х) = 0). То есть производная f(х) = x 5 + х — 160 примет такой вид: f’ (х) = 5x 4 +1.
2. Производная суммы двух слагаемых: (f+w)’ = f’w + fw’.
3. Производная логарифмической функции: (log_ad)’ = d/ln a*d. Эта формула применима ко всем видам логарифмов.
4. Производная степени: (x n )’= n*x n-1 . Например,(9x 2 )’ = 9*2x = 18x.
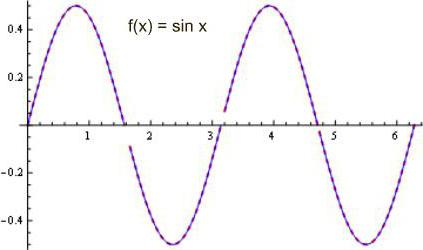
5. Производная синусоидальной функции: (sin a)’ = cos a. Если sin угла а равен 0,5, то ее производная равна √3/2.

Точки экстремума

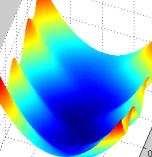
Мы уже разобрали, как найти точки минимума, однако существует понятие и точек максимума функции. Если минимум обозначает те точки, в которых функция переходит со знака минуса на плюс, то точками максимума являются те точки на оси абсцисс, на которых производная функции меняется с плюса на противоположный — минус.

Находить точки максимума можно по вышеописанному способу, только следует учесть, что они обозначают те участки, на которых функция начинает убывать, то есть производная будет меньше нуля.

В математике принято обобщать оба понятия, заменяя их словосочетанием «точки экстремумов». Когда в задании просят определить эти точки, это значит, что необходимо вычислить производную данной функции и найти точки минимума и максимума.

Источник

Способы определения минимума функции

Задачи поиска максимума эквивалентны задачам поиска минимума, так как требуется лишь поменять знак перед функцией. Для поиска минимума необходимо определить интервал, на котором функция могла бы иметь минимум. Для этого можно использовать (1) графическое представление функции, (2) аналитический анализ аппроксимирующей функции и (3) сведения о математической модели исследуемого процесса (т.е. законы поведения данной функции).

Численные методы поиска минимума функции одной переменной.

Определения.
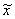
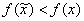
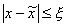
Функция f(x) имеет локальный минимум при некотором , если существует некоторая конечная ξ-окрестность этого элемента, в которой , . Требуется, чтобы на множестве X функция f(x) была по крайней мере кусочно-непрерывной.

Точка, в которой функция достигает наименьшего на множестве X значения, называется абсолютным минимумом функции. Для нахождения абсолютного минимума требуется найти все локальные минимумы и выбрать наименьшее значение.

Задачу называют детерминированной, если погрешностью вычисления (или экспериментального определения) функции f(x) можно пренебречь. В противном случае задачу называют стохастической. Все изложенные далее методы применимы только к детерминированным задачам.

Методы поиска минимума по нахождению корней уравнений.

Если функция f(x) аналитически дифференцируема, то решаем f / >(x) = 0 методами, изложенными в предыдущих главах. При этом условие f // (x) > 0 в найденной точке указывает нам на минимум. Для использования этих методов необходимо знать либо аналитический вид первой и второй производных, либо рассчитать их численно, если это не приведет к потере точности.

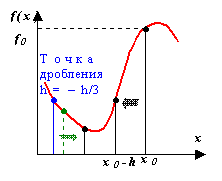
Наиболее простой метод поиска минимума. Пусть дана начальная точка x₀, а также величина и знак шага h, определяющие движение из этой точки в сторону предполагаемого минимума f(x). Метод заключается в последовательном дроблении исходного шага h с изменением его знака при выполнении условия f(x_k+1) > f(x_k), где k – порядковый номер вычисляемой точки. Например, как только очередное значение функции стало больше предыдущего, выполняется h = – h/3 и процесс продолжается до тех пор, пока

Данный метод является одним из самых медленных для поиска минимума. Основное достоинство данного алгоритма – возможность использования в программах управления экспериментальными исследованиями, когда значения функции f(x) последовательно измеряются с шагом h ≥ h_min.

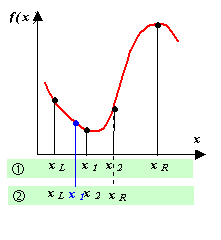
Метод золотого сечения.

Пусть f(x) задана и кусочно-непрерывна на [x_L, x_R], и имеет на этом отрезке только один локальный минимум. Золотое сечение, о котором упоминал ещё Евклид, состоит в разбиении интервала [ _L, x_R] точкой x₁ на две части таким образом, что отношение длины всего отрезка к его большей части равно отношению большей части к меньшей:

. (2)

Таким образом, возьмем на отрезке две точки x₁ и x₂, симметрично относительно границ делящие исходный отрезок в отношении золотого сечения:

,

,

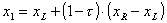
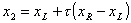
где коэффициент .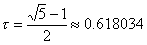

Если f(x)_{1 R} = x₂, в противном случае x_L = x₁. Оставшаяся внутри нового отрезка точка является первым приближением к минимуму и делит этот отрезок в отношении золотого сечения. Таким образом, на каждой итерации приближения к минимуму (см. рисунок) нам нужно ставить только одну точку (x₁ или x₂), в которой считать значение функции и сравнивать его с предыдущим. Условием выхода из итерационного процесса будет, подобно предыдущему случаю, условие |x₂ – x₁| ≤ ξ.

Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале.

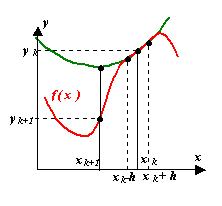
Пусть f(x) имеет первую и вторую производную. Разложим f(x) в ряд Тейлора в некоторой точке x_k, ограничиваясь при этом тремя членами разложения:

. (3)

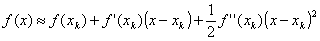
Иными словами, аппроксимируем нашу функцию в точке x_k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3): 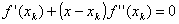. Пусть минимум аппроксимирующей параболы находится в точке x_k+1. Тогда вычислив значение функции f(x_k+1), мы получаем новую точку приближения к минимуму.

Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных f(x). Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагом h:

Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки x_k+h, x_k, x_k–h. Окончательное выражение, по которому можно строить итерационный процесс, таково:

. (4)

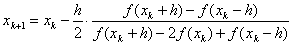
Данный метод отличается от вышеизложенных высокой скоростью сходимости. Вблизи экстремума, вплоть до расстояний

h 2 , сходимость практически не отличается от квадратичной. Однако алгоритм требует постоянного контроля сходимости. Например, итерационный процесс будет сходиться к минимуму, если

знаменатель формулы (4) должен быть >0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагают 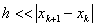. Иногда ради упрощения расчетов полагают 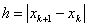, однако это существенно уменьшает скорость сходимости.

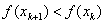. Если это не так, то от x_k следует сделать шаг 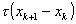с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.

Численные методы поиска минимума функции нескольких переменных.

Будем рассматривать методы поиска минимума 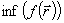в многомерных задачах на примере функции двух переменных f(x, y), так как эти методы легко аппроксимировать на случай трех и более измерений. Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает. Разные методы отличаются способами построения таких траекторий, так как метод, приспособленный к одному типу рельефа, может оказаться плохим для рельефа другого типа. Различают следующие типы рельефа:

1) Котловинный
(гладкая функция)

2) Истинный овраг

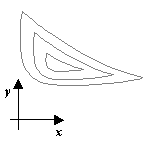
3) Разрешимый овраг

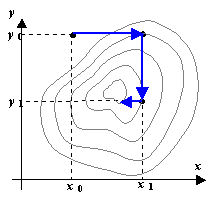
Метод координатного спуска.

Пусть требуется найти минимум f(x, y). Выберем нулевое приближение (x₀ , y₀). Рассмотрим функцию одной переменной f(x, y₀) и найдем ее минимум, используя любой из рассмотренных выше способов. Пусть этот минимум оказался в точке (x₁ , y₀). Теперь точно так же будем искать минимум функции одной переменной f(x₁ , y). Этот минимум окажется в точке (x₁ , y₁). Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполнится условие

Сходимость метода зависит от вида функции и выбора нулевого приближения. Вблизи невырожденного минимума гладкой функции спуск по координатам линейно сходится к минимуму. Если линии уровня образуют истинный овраг, возможен случай, когда спуск по одной координате приводит на дно оврага, а любое движение по следующей координате ведет на подъем. Процесс координатного спуска в данном случае не сходится к минимуму.
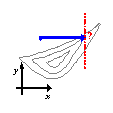
При попадании траектории спуска в разрешимый овраг сходимость становится чрезвычайно медленной. В физических задачах овражный рельеф указывает на то, что не учтена какая-то закономерность, определяющая связь между переменными. Явный учет этой закономерности облегчает использование численных методов.

Метод градиентного (наискорейшего) спуска.

В этом методе функция минимизируется по направлению, в котором она быстрее всего убывает, т.е. в направлении, обратном . Вдоль этого направления функция зависит от одной параметрической переменной t, для нахождения минимума которой можно воспользоваться любым известным методом поиска минимума функции одной переменной. Спуск из точки начального приближения против градиента до минимума t определяет новую точку , в которой вновь определяется градиент и делается следующий спуск. Условием окончания процесса, как и в случае координатного спуска, будет .

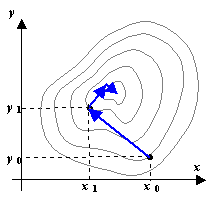
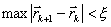
С помощью метода градиентного спуска минимум гладких функций в общем случае находится быстрее, чем при использовании координатного спуска, однако нахождение градиента численными методами может свести на нет полученный выигрыш. Сходимость плохая для функций с овражным рельефом, т.е. с точки зрения сходимости градиентный спуск не лучше спуска по координатам.

Каждый спуск заканчивается в точке, где линия градиента касательна к линии (поверхности) уровня. Это означает, что каждый следующий спуск должен быть перпендикулярен предыдущему. Таким образом, вместо поиска градиента в каждой новой точке можно сосчитать градиент в начальной точке, и развернуть оси координат так, чтобы одна их осей была параллельна градиенту, а затем осуществлять спуск координатным методом.

Ставится задача найти минимум для овражной функции. Для этого выбираются две близкие точки и , и осуществляется спуск из этих точек (любым методом), причем высокой точности сходимости не требуется. Конечные точки спуска и будут лежать вблизи дна оврага. Затем осуществляется движение вдоль прямой, соединяющей и в сторону уменьшения (как бы вблизи дна оврага). Движение может быть осуществлено только на один шаг

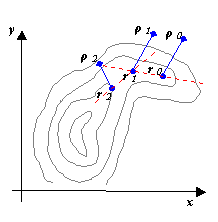
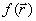
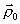
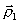
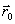
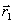
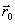
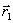
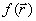
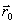
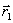
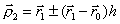
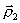
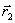
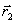
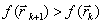
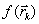
h, направление выбирается из сравнения значения функции в точках и . Таким образом, находится новая точка . Так как возможно, что точка уже лежит на склоне оврага, а не на дне, то из нее снова осуществляется спуск в новую точку . Затем намечается новый путь по дну оврага вдоль прямой, соединяющей и . Если – процесс прекращается, а в качестве минимума в данном овраге используется значение .

Метод оврагов рассчитан на то, чтобы пройти вдоль оврага и выйти в котловину около минимума. В этой котловине значения минимума лучше уточнять другими методами.

Проблемы поиска минимума в задачах с большим числом измерений.

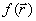
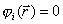
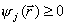
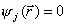
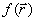
Пусть в n-мерном векторном пространстве задана скалярная функция . Наложим дополнительные условия , 1 ≤ i ≤ m; , 1 ≤ j ≤ p. Условия типа равенств выделяют в пространстве некоторую (n – m)-мерную поверхность, а условия типа неравенств выделяют n-мерную область, ограниченную гиперповерхностями . Число таких условий может быть произвольным. Следовательно, задача inf есть поиск минимума функции n переменных в некоторой (n – m)-мерной области E. Функция может достигать минимального значения как внутри области, так и на ее границе. Однако перейти к (n – m)-мерной системе координат практически никогда не удается, поэтому спуск приходится вести во всем n-мерном пространстве.

Даже если нулевое приближение лежит в области E, естественная траектория спуска сразу выходит из этой области. Для принудительного возврата процесса в область E, например, используется метод штрафных функций: к 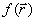прибавляются члены, равные нулю в E, и возрастающие при нарушении дополнительных условий (ограничений). Метод прост и универсален, однако считается недостаточно надежным. Более качественный результат дает использование симплекс-методов линейного программирования, однако данный вопрос в рамках настоящего курса не рассматривается.

Источник