Способы определения критической точки

Точка безубыточности (Критическая точка). Понятие. Способ определения. Вывод формулы. Графическая интерпретация

Точка безубыточности — минимальный объём производства и реализации продукции, при котором расходы будут компенсированы доходами, а при производстве и реализации каждой последующей единицы продукции предприятие начинает получать прибыль. Точку безубыточности можно определить в единицах продукции, в денежном выражении или с учётом ожидаемого размера прибыли.

Точка безубыточности в денежном выражении — такая минимальная величина дохода, при которой полностью окупаются все издержки (прибыль при этом равна нулю):

,

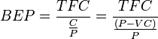
Где BEP (англ. break-even

point) — точка безубыточности,

TFC— величина постоянных издержек,

VC— величина переменных издержек на единицу продукции,

P— стоимость единицы продукции (реализация),

C— прибыль с единицы продукции без учёта доли постоянных издержек (разница между стоимостью продукции (P) и переменными издержками на единицу продукции (VC)).

Можно заметить, что выражение численно равно отношению валовой маржи к выручке.

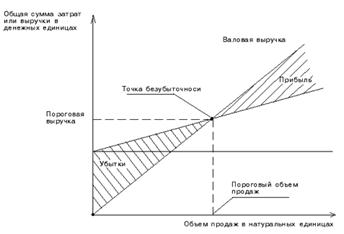
Расчет точки безубыточности основывается на взаимосвязи трех показателей: «затраты — объем продаж — прибыль». Определить взаимодействие этих показателей можно графически:

— по оси абсцисс графика указывается объем реализации;

— по оси ординат — себестоимость реализованной продукции плюс прибыль, которые составляют выручку от реализации.

Последовательность построения графика «затраты — объем — прибыль» (СУР-графика) такова:

— на графике проводится пря­мая постоянных затрат (прямая, параллельная оси абсцисс);

— выбирается точка на оси абсцисс (величина объема строи­тельства);

— проводится прямая переменных затрат, соответ­ствующая выбранному объему строительства;

— затем прово­дится прямая выручки от реализации выбранного объема производства.

Точка пересечения прямых переменных затрат и выручки от реализации является точкой безубыточности. (Рисунок 1)

Изображенная на рисунке точка безубыточности (порога рентабельности) – это точка (продаж). Если предприятие продает продукции меньше порогового объема продаж, то оно терпит убытки, если больше – получает прибыль.

По графику можно установить, при каком объеме реализации организация получит прибыль, при каком — нет, а также точку, в которой затраты будут равны выручке от реализации (точку безубыточности или порог рентабельности), ниже кото­рой производство будет убыточным. Это точка пересечения прямой общих затрат и прямой доходов.

Однородные (простые) и комплексные (сложные) статьи расходов. Понятие. Подразделение статей расходов на однородные и комплексные. Перечень и состав основных комплексных статей расходов.

Однородные (простые) статьи состоят из одного вида затрат: например, “сырье и материалы” или “Основная заработная плата рабочих, занятых в производственном процессе”. Простые статьи рассчитываются на основе норм и нормативов материальных и трудовых затрат, цен и тарифов на материально-энергетические затраты, расценок по заработной плате.

Комплексные (сложные) статьи представляют собой набор затрат. Показатель статьи калькуляции складывается как итоговый показатель соответствующей сметы. Например “Общепроизводственные расходы”.

Таким образом, деление затрат на простые и комплексные определяет выбор методики расчета статей калькуляции.

Основные группы комплексных расходов в составе себестоимости продукции:

— Общепроизводственные расходы (ОПР).

— Общехозяйственные расходы (ОХР).

— Потери от брака.

— Прочие производственные расходы.

— Коммерческие расходы (расходы на продажу) (КР).

Задачи анализа комплексных статей затрат:

· изучение их динамики и соблюдения сметных расходов;

· выявление причин отклонений в динамике от сметы соответствующих статей затрат;

· определение влияния изменений технического уровня и организации производства и труда на уровень рассматриваемых расходов;

· выявление резервов снижения себестоимости продукции в части комплексных затрат.

14 основных комплексных статей.

1. Транспортные расходы.

2. Расходы на оплату труда.

3. Отчисления на социальные нужды.

4. Расходы на аренду и содержание зданий, сооружений, помещений, оборудования и инвентаря.

5. Амортизация основных средств.

6. Расходы на ремонт основных средств.

7. Износ санитарной и специальной одежды, столового белья, посуды, приборов, других малоценных и быстроизнашивающихся предметов.

8. Расходы на топливо, газ, электроэнергию для производственных нужд.

9. Расходы на хранение, подработку, подсортировку и упаковку товаров.

10. Расходы на рекламу.

11. Затраты по оплате процентов за пользование займом.

12. Потери товаров и технологические отходы.

Источник

Критические точки, точки экстремумафункции

Содержимое разработки

Специализированная гимназия № 8 с обучением на трех языках имени М.Х. Дулати

Алгебра и начала анализа

Критические точки и

Л.С. Атанасян. Геометрия 10-11

Харченко Татьяна Викторовна

— знать определения критических точек и точек экстремума функции, условие существования экстремума функции.

Л.С. Атанасян. Геометрия 10-11

— Использует определение находит критические (стационарные) точки, используя определение;

— применяет необходимое и достаточное условие для определение точек экстремума функции.

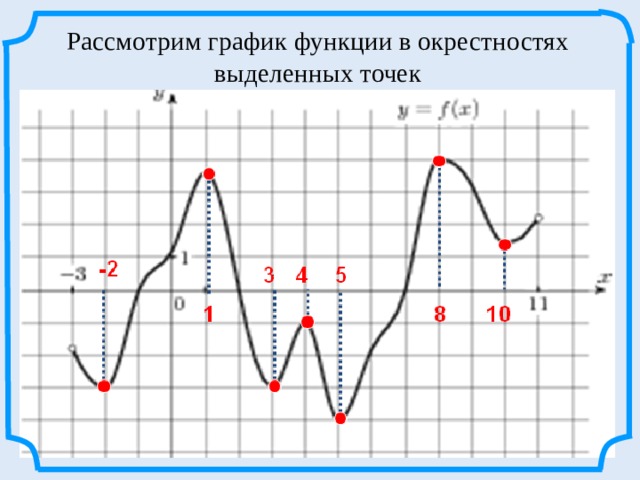
Рассмотрим график функции в окрестностях выделенных точек

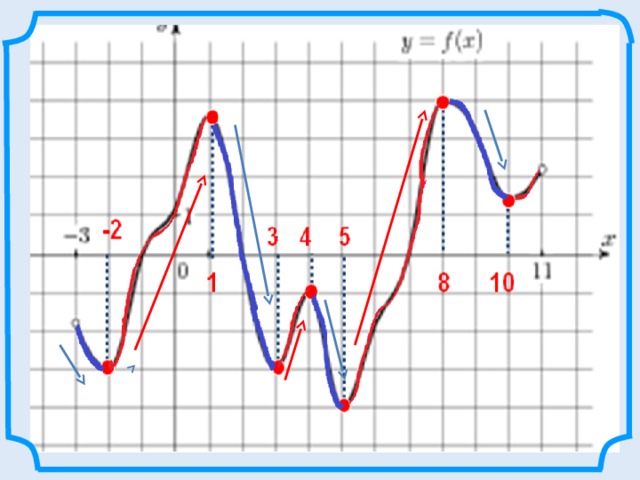
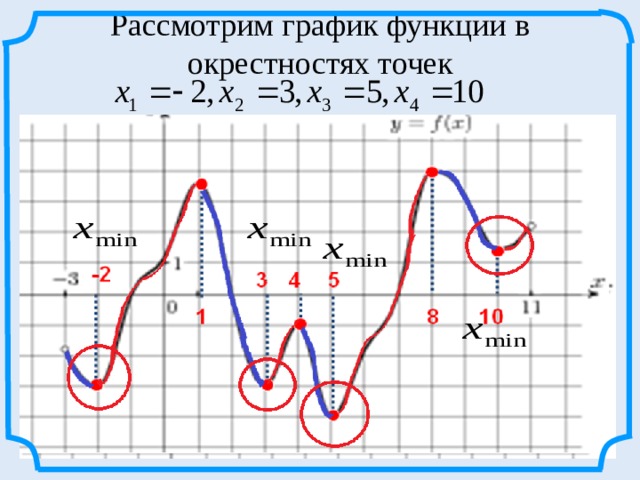
Рассмотрим график функции в окрестностях точек

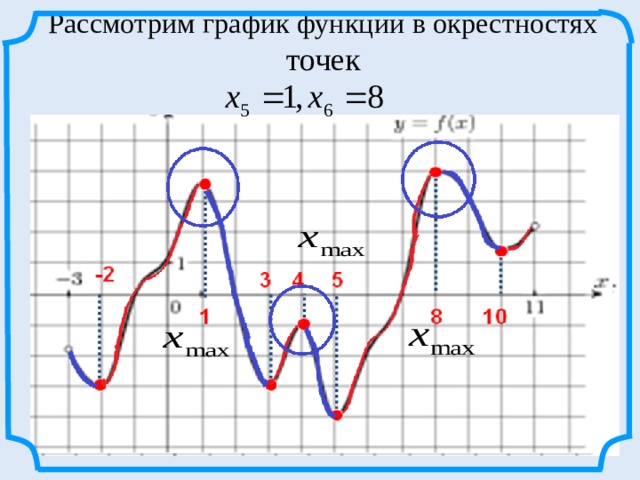
Рассмотрим график функции в окрестностях точек

f( х 0 ) » width=»640″

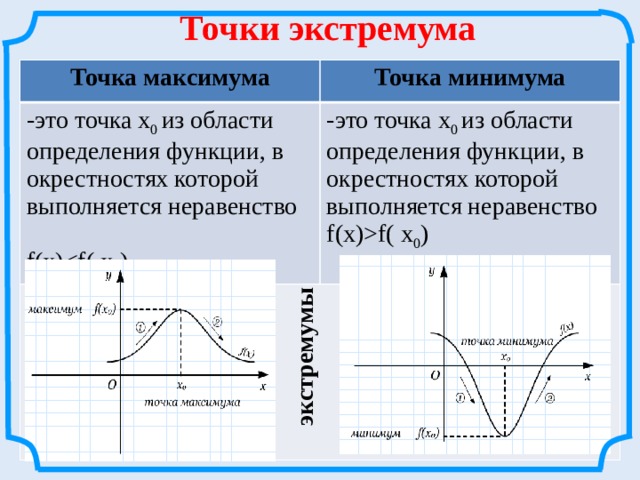
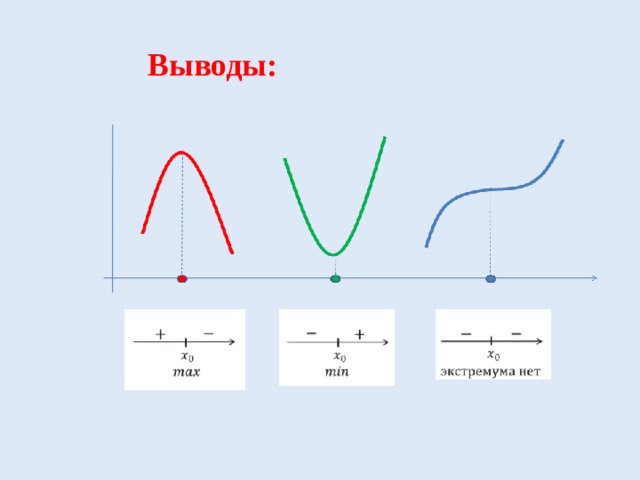
-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство

-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство f(x)f( х 0 )

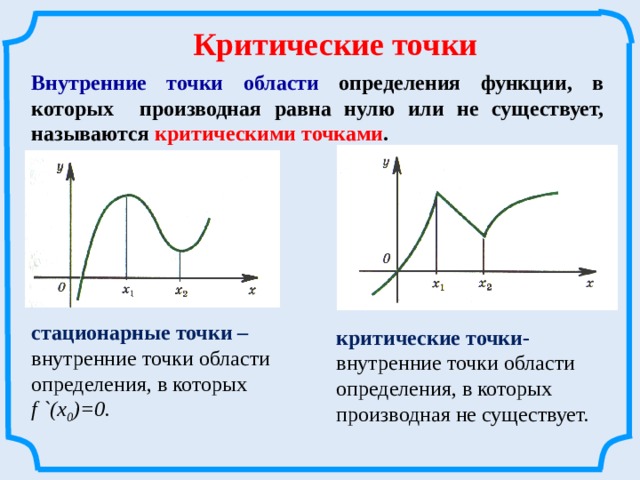
Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками .

внутренние точки области

определения, в которых f `(х 0 )=0.

критические точки- внутренние точки области

определения, в которых производная не существует.

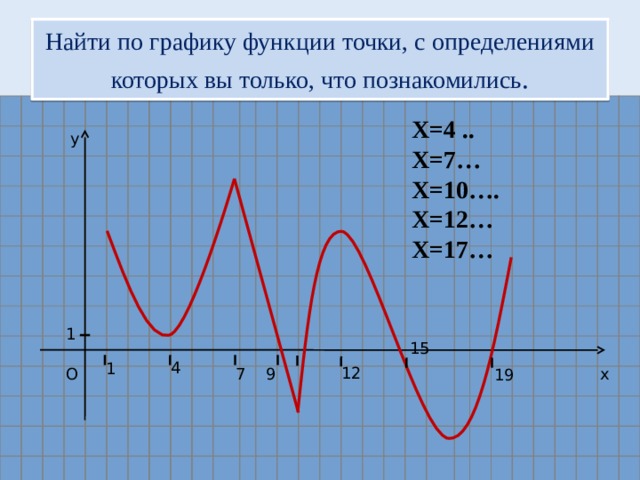
Найти по графику функции точки, с определениями которых вы только, что познакомились .

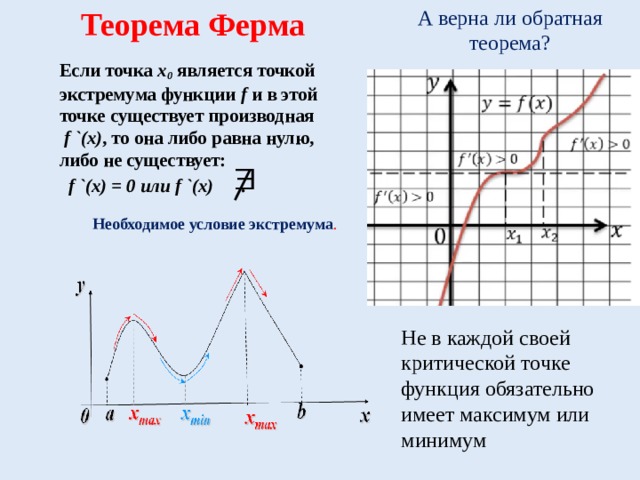
А верна ли обратная теорема?

Если точка х 0 является точкой экстремума функции f и в этой точке существует производная f `(x) , то она либо равна нулю, либо не существует:

Необходимое условие экстремума .

Не в каждой своей критической точке функция обязательно имеет максимум или минимум

0 на интервале (а; х 0 ), и f `(x) на интервале (х 0 ; b), то точка х 0 является точкой максимума функции f. Признак минимума функции. Если функция у= f((х) непрерывна в точке х 0 , f `(x) на интервале (а; х 0 ) и f `(x) 0 на интервале (х 0 ; b) , то точка х 0 является точкой минимума функции f » width=»640″

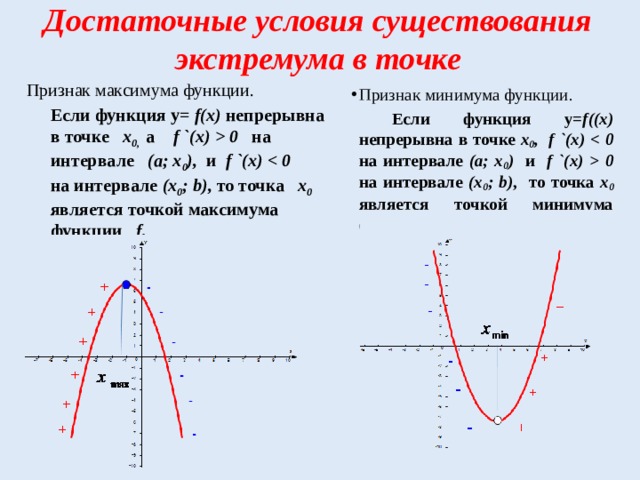
Достаточные условия существования экстремума в точке

Признак максимума функции.

• Признак минимума функции.

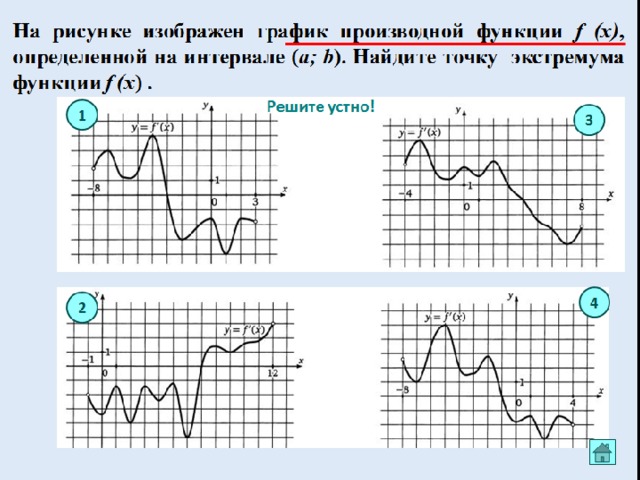
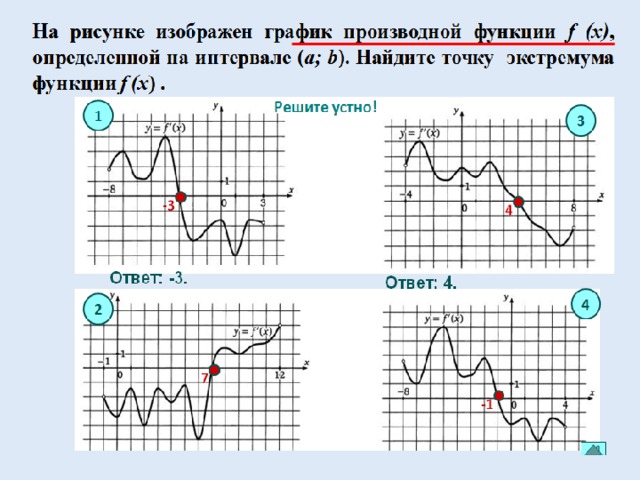
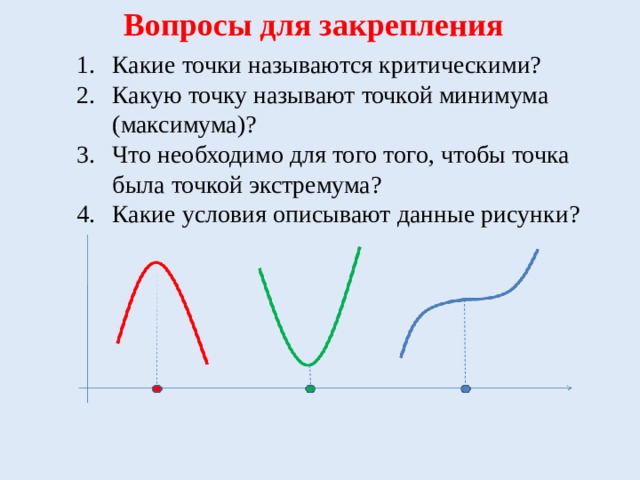
Вопросы для закрепления

• Какие точки называются критическими?
• Какую точку называют точкой минимума (максимума)?
• Что необходимо для того того, чтобы точка была точкой экстремума?
• Какие условия описывают данные рисунки?

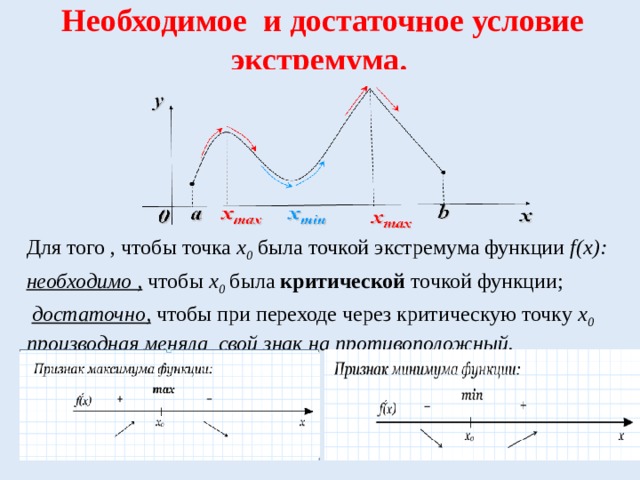
Необходимое и достаточное условие экстремума.

Для того , чтобы точка х 0 была точкой экстремума функции f(х):

необходимо , чтобы х 0 была критической точкой функции;

достаточно, чтобы при переходе через критическую точку х 0 производная меняла свой знак на противоположный.

Найдите точку минимума функции

Найдите точку максимума функции

Задания для самостоятельного решения

1А. (5б) Найдите критические точки функции. Выясните, какие из этих точек являются:

а) точками минимума; б) точками максимума.

Находит правильно производную

Находит критические точки

Расставляет верно знаки производной

Определяет точки минимума

Определяет точки максимума

Задания для самостоятельного решения

2Б. (6б) Найдите экстремумы функции:

Находит область определения

Находит правильно производную

Находит критические точки

Расставляет верно знаки производной

Определяет точки экстремума

Находит экстремумы функции

Задания для самостоятельного решения

3С.(7б)Найдите промежутки возрастания и убывания, точки экстремума функции:

Находит область определения

Находит критические точки

Расставляет знаки производной

Исследует поведение функции

Находит промежутки монотонности

Определяет точки экстремума

Дополнительные цифровые ресурсы

Ссылки на дополнительные ресурсы для самообразования

https:// bilimland.kz /ru/subject/algebra/10-klass/kriticheskie-tochki-dostatochnoe-uslovie-sushestvovaniya-ehkstremuma?mid=%info%

https:// www.yaklass.ru/ p/algebra/10-klass/proizvodnaia-9147/primenenie-proizvodnoi-dlia-issledovaniia-funktcii-na-monotonnost-i-ekstr_-11226

Рефлексия содержания учебного материала

Сегодня я узнал…

Дорогие дети! Вы получили самое основное содержание по новой теме, другие материалы вы получите от своего учителя! Если у вас есть вопросы, вы их можете задать учителю! Удачи в освоении нового материала, наши юные друзья!

Источник

Критическая точка (математика) — Critical point (mathematics)

Критическая точка — это широкий термин, используемый во многих областях математики .

При работе с функциями действительного переменного , критическая точка является точкой в области функции , где функция либо не дифференцируема или производная равна нулю. При работе с комплексными переменными , критической точкой является, так же, точкой в области функции, где она либо не голоморфна или производная равна нуль. Аналогично, для функции нескольких действительных переменных , А критической точкой является значением в своей области , где градиент не определен или равен нулю.

Значение функции в критической точке является критическим значением .

Такое определение распространяется на дифференцируемые отображения между R м и R п , в критической точке бытием, в данном случае, в точке , где ранг из матрицы Якоби не максимален. Он распространяется далее на дифференцируемые отображения между дифференцируемыми многообразиями как точки, в которых ранг матрицы Якоби уменьшается. В этом случае критические точки также называют точками бифуркации .

В частности, если C — плоская кривая , определяемая неявным уравнением f ( x , y ) = 0, критические точки проекции на ось x , параллельную оси y, являются точками, в которых касательная к C параллельны оси y , то есть точкам, где . Другими словами, критические точки — это те, в которых теорема о неявной функции неприменима. ∂ ж ∂ у ( Икс , у ) знак равно 0 <\ displaystyle <\ frac <\ partial f><\ partial y>> (x, y) = 0>

Понятие критической точки позволяет математически описать астрономическое явление, которое было необъяснимо до времени Коперника . Стационарная точка на орбите планеты является точка траектории планеты на небесной сфере , где движение планеты , кажется, остановить перед перезапуском в другом направлении. Это происходит из-за критической точки проекции орбиты в окружность эклиптики .

СОДЕРЖАНИЕ

Критическая точка функции одной переменной

Критическая точка функции из одной вещественной переменной , ф ( х ), это значение х ₀ в области от F , где она не дифференцируема или его производное , равно 0 ( е ‘( х ₀ ) = 0). Критическое значение является образом при F критической точки. Эти понятия могут быть визуализированы с помощью графика из F : в критической точке, график имеет горизонтальную касательную , если можно назначить один на всех.

Обратите внимание на то, как, для дифференцируемой функции , критическая точка такой же , как стационарная точка .

Хотя это легко визуализировать на графике (который представляет собой кривую), понятие критической точки функции не следует путать с понятием критической точки в некотором направлении кривой ( подробное определение см. Ниже ). Если g ( x , y ) — дифференцируемая функция двух переменных, то g ( x , y ) = 0 — неявное уравнение кривой. Критическая точка такой кривой, для проекции параллельно у оси х (отображение ( х , у ) → х ), является точкой кривой , где . Это означает, что касательная к кривой параллельна оси y , и что в этой точке g не определяет неявную функцию от x до y (см. Теорему о неявной функции ). Если ( x ₀ , y ₀ ) — такая критическая точка, то x ₀ — соответствующее критическое значение . Такая критическая точка также называется точкой бифуркации , поскольку, как правило, при изменении x появляются две ветви кривой на стороне x ₀ и ноль на другой стороне. ∂ грамм ∂ у ( Икс , у ) знак равно 0 <\ displaystyle <\ frac <\ partial g><\ partial y>> (x, y) = 0>

Из этих определений следует, что дифференцируемая функция f ( x ) имеет критическую точку x ₀ с критическим значением y ₀ тогда и только тогда, когда ( x ₀ , y ₀ ) является критической точкой ее графика для проекции, параллельной x -оси с тем же критическим значением y ₀ . Если f не дифференцируема в точке x ₀ из-за того, что касательная становится параллельной оси y, то x ₀ снова является критической точкой f , но теперь (x ₀ , y ₀ ) является критической точкой его графика для проекции параллельно оси y .

Например, критические точки единичной окружности уравнения x 2 + y 2 — 1 = 0 — это (0, 1) и (0, -1) для проекции, параллельной оси x , и (1, 0) и (-1, 0) для направления, параллельного оси y . Если рассматривать верхний полукруг как график функции , то x = 0 — критическая точка с критическим значением 1 из-за того, что производная равна 0, а x = -1 и x = 1 — критические точки с критическим значением 0 из-за того, что производная не определена. ж ( Икс ) знак равно 1 — Икс 2 <\ displaystyle f (x) = <\ sqrt <1-x ^ <2>>>>

Примеры

• Функция f ( x ) = x 2 + 2 x + 3 дифференцируема всюду с производной f ′ ( x ) = 2 x + 2. Эта функция имеет единственную критическую точку −1, поскольку это единственное число x_0. для которых 2 х₀ + 2 = 0. Эта точка является глобальным минимумом из F . Соответствующее критическое значение равно f (−1) = 2. График f представляет собой вогнутую вверх параболу , критическая точка — это абсцисса вершины, где касательная линия горизонтальна, а критическое значение — ордината вершины. и может быть представлен пересечением этой касательной линии и оси y .
• Функция f ( x ) = x 2/3 определена для всех x и дифференцируема при x ≠ 0 с производной f ′ ( x ) = 2 x −1/3 / 3. Поскольку f не дифференцируема при x = 0 и f ‘(x) ≠ 0 в противном случае, это единственная критическая точка. График функции F имеет излом в этой точке с вертикальной касательной. Соответствующее критическое значение f (0) = 0.
• Функция абсолютного значения f (x) = | x | дифференцируема всюду, кроме критической точки x = 0, где она имеет точку глобального минимума с критическим значением 0.
• Функция f ( x ) = 1 / x не имеет критических точек. Точка x = 0 не является критической, потому что она не входит в область определения функции.

Расположение критических точек

По теореме Гаусса-Лукас , все критических точек полиномиальной функции в в комплексной плоскости находятся внутри выпуклая оболочка из корней функции. Таким образом, для полиномиальной функции только с действительными корнями все критические точки действительны и находятся между наибольшим и наименьшим корнями.

Гипотеза Сендова утверждает, что если все корни функции лежат в единичном круге на комплексной плоскости, то существует по крайней мере одна критическая точка в пределах единичного расстояния от любого заданного корня.

Критические точки неявной кривой

Критические точки играют важную роль в изучении плоских кривых , определяемое неявными уравнениями , в частности , для черчения их и определить их топологию . Понятие критической точки, которое используется в этом разделе, может показаться отличным от того, что использовалось в предыдущем разделе. Фактически это конкретизация простого случая приведенного ниже общего понятия критической точки .

Таким образом, мы рассматриваем кривую C, определяемую неявным уравнением , где f — дифференцируемая функция двух переменных, обычно двумерный многочлен . Точки кривой — это точки евклидовой плоскости , декартовы координаты которых удовлетворяют уравнению. Есть две стандартные проекции и , определяемые и, которые отображают кривую на оси координат . Их называют проекцией, параллельной оси y, и проекцией, параллельной оси x , соответственно. ж ( Икс , у ) знак равно 0 <\ displaystyle f (x, y) = 0> π у <\ displaystyle \ pi _ > π Икс <\ displaystyle \ pi _ > π у ( ( Икс , у ) ) знак равно Икс <\ Displaystyle \ пи _ <у>((х, у)) = х> π Икс ( ( Икс , у ) ) знак равно у , <\ Displaystyle \ пи _ <х>((х, у)) = у,>

Точка C является критической для , если касательная к C существует и параллельна оси y . В этом случае изображения по критической точки и касательной те же точки х Оу, называется критическим значением . Таким образом, точка является критической для, если ее координаты являются решением системы уравнений : π у <\ displaystyle \ pi _ > π у <\ displaystyle \ pi _ > π у <\ displaystyle \ pi _ >

ж ( Икс , у ) знак равно ∂ ж ∂ у ( Икс , у ) знак равно 0 <\ displaystyle f (x, y) = <\ frac <\ partial f><\ partial y>> (x, y) = 0>

Отсюда следует, что данное определение является частным случаем общего определения критической точки, которое дается ниже .

Определение критической точки аналогично. Если C — график функции , то ( x , y ) является критическим тогда и только тогда, когда x является критической точкой g , и что критические значения совпадают. π Икс <\ displaystyle \ pi _ > у знак равно грамм ( Икс ) <\ Displaystyle у = г (х)> π Икс <\ displaystyle \ pi _ >

Некоторые авторы определяют критические точки из С как точками , которые имеют решающее значение для любого или , хотя они зависят не только от С , но и от выбора осей координат. Также от авторов зависит, будут ли особые точки рассматриваться как критические. Фактически особые точки — это точки, удовлетворяющие π Икс <\ displaystyle \ pi _ > π у <\ displaystyle \ pi _ >

ж ( Икс , у ) знак равно ∂ ж ∂ Икс ( Икс , у ) знак равно ∂ ж ∂ у ( Икс , у ) знак равно 0 <\ displaystyle f (x, y) = <\ frac <\ partial f><\ partial x>> (x, y) = <\ frac <\ partial f><\ partial y>> (x, y) = 0> ,

и, таким образом, являются решениями любой системы уравнений, характеризующих критические точки. В этом более общем определении критические точки для — это именно те точки, где теорема о неявной функции не применяется. π у <\ displaystyle \ pi _ >

Использование дискриминанта

Когда кривая C является алгебраической, то есть когда она определяется двумерным многочленом f , дискриминант является полезным инструментом для вычисления критических точек.

Здесь мы рассматриваем только проекцию ; Аналогичные результаты применимы к замене x и y . π у <\ displaystyle \ pi _ > π Икс <\ displaystyle \ pi _ >

Пусть будет дискриминант из F рассматривается как многочлен у с коэффициентами , которые являются многочленами от х . Таким образом, этот дискриминант является многочленом от x, который имеет критические значения среди своих корней. Диск у ⁡ ( ж ) <\ displaystyle \ operatorname _ (f)> π у <\ displaystyle \ pi _ >

Точнее, простой корень либо критическое значение такой соответствующей критической точки является точка , которая не является особой , ни точки перегиба, или х координаты на асимптоте , которая параллельна у оси х и касается » на бесконечности »до точки перегиба (асимптота перегиба). Диск у ⁡ ( ж ) <\ displaystyle \ operatorname _ (f)> π у <\ displaystyle \ pi _ >

Множественный корень дискриминанта соответствует либо нескольким критическим точкам, либо асимптотам перегиба, имеющим одно и то же критическое значение, либо критической точке, которая также является точкой перегиба, либо особой точке.

Несколько переменных

Для функции нескольких вещественных переменных точка P (то есть набор значений для входных переменных, который рассматривается как точка в R n ) является критической, если это точка, в которой градиент не определен или градиент равен нулю. . Критические значения — это значения функции в критических точках.

Критическая точка (где функция дифференцируема) может быть либо локальным максимумом , либо локальным минимумом, либо седловой точкой . Если функция по меньшей мере , дважды непрерывно дифференцируемые различные случаи могут быть выделены путем рассмотрения собственных значений на гессенском матрицы вторых производных.

Критическая точка, в которой матрица Гессе невырождена , называется невырожденной , а знаки собственных значений гессиана определяют локальное поведение функции. В случае функции одной переменной гессиан — это просто вторая производная , рассматриваемая как матрица 1 × 1, которая неособа тогда и только тогда, когда она не равна нулю. В этом случае невырожденная критическая точка является локальным максимумом или локальным минимумом, в зависимости от знака второй производной, которая положительна для локального минимума и отрицательна для локального максимума. Если вторая производная равна нулю, критическая точка обычно является точкой перегиба , но также может быть точкой волнистости , которая может быть локальным минимумом или локальным максимумом.

Для функции n переменных количество отрицательных собственных значений матрицы Гессе в критической точке называется индексом критической точки. Невырожденная критическая точка является локальным максимумом тогда и только тогда, когда индекс равен n , или, что то же самое, если матрица Гессе отрицательно определена ; это локальный минимум, если индекс равен нулю или, что то же самое, если матрица Гессе положительно определена . Для других значений индекса невырожденная критическая точка — это седловая точка , то есть точка, которая является максимумом в одних направлениях и минимумом в других.

Приложение к оптимизации

По теореме Ферма все локальные максимумы и минимумы непрерывной функции находятся в критических точках. Следовательно, чтобы найти локальные максимумы и минимумы дифференцируемой функции, теоретически достаточно вычислить нули градиента и собственные значения матрицы Гессе в этих нулях. Это не очень хорошо работает на практике , поскольку она требует решений в нелинейную систему из системы уравнений , которая является сложной задачей. Обычные численные алгоритмы гораздо более эффективны для поиска локальных экстремумов, но не могут подтвердить, что были найдены все экстремумы. В частности, при глобальной оптимизации эти методы не могут подтвердить, что результат действительно является глобальным оптимумом.

Когда минимизируемая функция является многомерным полиномом , критические точки и критические значения являются решениями системы полиномиальных уравнений , и современные алгоритмы решения таких систем обеспечивают конкурентоспособные сертифицированные методы поиска глобального минимума.

Критическая точка дифференцируемой карты

Учитывая дифференцируемое отображение F из R т в R п , то критические точки из F являются точками R м , где ранг матрицы Якоби из F не является максимальным. Изображение критической точки при f называется критическим значением . Точка в дополнении набора критических значений называется регулярным значением . Теорема Сарда утверждает, что множество критических значений гладкого отображения имеет нулевую меру .

Некоторые авторы дают несколько иное определение: критическая точка из F является точкой R м , где ранг матрицы Якоби из F меньше , чем п . Согласно этому соглашению, все точки являются критическими, когда m V и W соответствующих размерностей m и n . В окрестностях точки р из V и в е ( р ) , графики являются диффеоморфизмами и точка р является критическим для F , если имеет решающее значение для этого определения не зависит от выбора диаграмм , так как переходы карты , являющихся диффеоморфизмов, их Якобиевы матрицы обратимы, и умножение на них не меняет ранг якобиевой матрицы. Если M — гильбертово многообразие (не обязательно конечномерное) и f — вещественнозначная функция, то мы говорим, что p — критическая точка f, если е это не погружение в воду на р . ж : V → W <\ displaystyle f: V \ rightarrow W> φ : V → р м <\ displaystyle \ varphi: V \ rightarrow \ mathbf ^ > ψ : W → р п . <\ displaystyle \ psi: W \ rightarrow \ mathbf ^ .> φ ( п ) <\ displaystyle \ varphi (p)> ψ ∘ ж ∘ φ — 1 . <\ displaystyle \ psi \ circ f \ circ \ varphi ^ <- 1>.> ψ ∘ ж ∘ φ — 1 . <\ displaystyle \ psi \ circ f \ circ \ varphi ^ <- 1>.>

Приложение к топологии

Критические точки имеют основополагающее значение для изучения топологии из многообразия и вещественных алгебраических многообразий . В частности, они являются основным инструментом для теории Морса и теории катастроф .

Связь между критическими точками и топологией появляется уже на более низком уровне абстракции. Пусть , например, быть суб-многообразие и Р будет точкой вне квадрата расстояния до P из точки является дифференциальной картой таким образом, что каждая компонента связности содержит , по меньшей мере , критическую точку, где расстояние является минимальным. Отсюда следует, что число связных компонент матрицы ограничено сверху числом критических точек. V <\ displaystyle V> р п , <\ displaystyle \ mathbb ^ ,> V . <\ displaystyle V.> V <\ displaystyle V> V <\ displaystyle V> V <\ displaystyle V>

В случае вещественных алгебраических многообразий это наблюдение, связанное с теоремой Безу, позволяет нам ограничить количество компонент связности функцией степеней многочленов, определяющих многообразие.

Источник