Пособие для студента (для строительных специальностей)
Загрузить всю книгу 
Титульный лист
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Тольяттинский государственный университет
Кафедра «Материаловедение и механика материалов»
ПОСОБИЕ ДЛЯ СТУДЕНТА
в рамках технологии 30/70
Авторы-составители: к.т.н., доцент Т.Ф.Гаврилова, к.ф.-м.н., доцент Е.П.Гордиенко, преп. С.А.Тимофеев.
Под общей редакцией д.ф.-м.н. Мерсона Д.Л.
Пособие для студента по дисциплине «Сопротивление материалов» в рамках технологии 30/70. Часть I: Методическое пособие / Составители: Т.Ф.Гаврилова, Е.П.Гордиенко, С.А.Тимофеев / под ред. д.ф.-м.н. Мерсона Д.Л. Тольятти: ТГУ, 2005. — 80 с.
Методическое пособие предназначено для оказания помощи студентам в организации самостоятельной работы при изучении дисциплины «Сопротивление материалов» в рамках технологии 30/70 (часть I – 1-й семестр).
Дано описание модульной конструкции дисциплины, представлены: технологическая карта дисциплины, алгоритмы работы в каждом модуле, рейтинговая система оценки знаний, методическое обеспечение модулей (по содержанию 1-го семестра обучения).
Пособие дает студенту полные сведения о содержании и последовательности изучения курса «Сопротивление материалов», формах аудиторной и самостоятельной работы, требованиях к знаниям и умениям, формах отчетности. Позволяет планировать и прогнозировать результаты процесса обучения.
Методическое пособие предназначено для студентов строительных специальностей.
Утверждено научно-методическим советом Тольяттинского государственного университета.
Подписано в печать 27.07.2005 Формат 240
170
Печать оперативная. Уч.п.л. 5. Уч.-изд.л. 4,65.
ã Тольяттинский государственный университет, 2005
Источник
Определение центра тяжести сложной плоской фигуры.
Положение центра тяжести сложной плоской фигуры определяется координатным способом по следующему правилу:
- Сложная фигура разбивается на составные части, представляющие собой простые геометрические фигуры. При этом желательно, чтобы количество составных частей было минимальным.
- Определяются площади составных частей. При этом необходимо помнить, что площадь вырезанной фигуры считается отрицательной.
- Выбирается система координат, связанная с заданной фигурой, обозначаются на чертеже центры тяжести составных частей и определяются их координаты в выбранной системе координат.
- Определяются координаты центра тяжести всей фигуры по формулам:
, где
— координаты центров тяжести составных частей;
— площади составных частей.
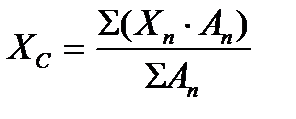
Удобно результаты занести в таблицу
5. По полученным координатам обозначается на чертеже фигуры её центр тяжести.
Примеры решения задачи.
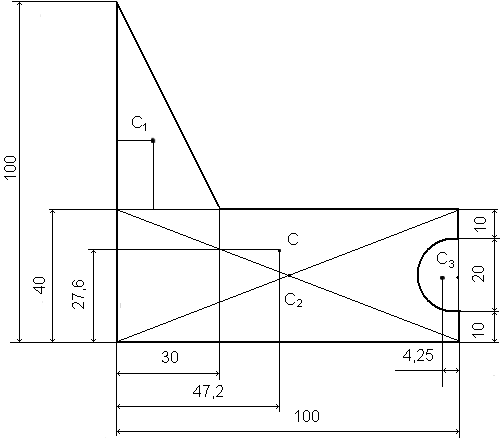
ПРИМЕР 1. Сложная фигура состоит из простых геометрических фигур (рисунок 23).
Рисунок 23. Сложная плоская фигура.
1. Разбиваем заданную плоскую фигуру на простые составные части:
1- прямоугольный треугольник, 2- прямоугольник, 3- круговой сектор (вырезан).
2. Определяем площади каждой составной части:
Площадь прямоугольного треугольника равна половине произведения его катетов.
мм 2 .
Площадь прямоугольника равна произведению его сторон:
мм 2 .
Площадь кругового сектора, представляющего половину круга, равна:
мм 2 .
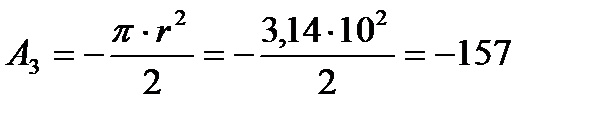
3. Выбираем систему координат так, чтобы вся фигура расположилась в первой координатной четверти. Обозначим на чертеже фигуры центры тяжести составных частей (рисунок 19) и определим их координаты:
мм, 
мм — координаты центра тяжести треугольника.
мм, 
мм — координаты центра тяжести прямоугольника.
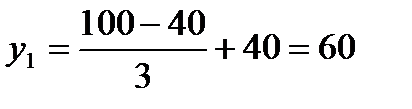
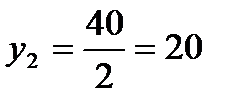
| Фигура | Xn мм. | Yn мм. | An мм 2 |
| Треугольник | 10 | 60 | 900 |
| Прямоугольник | 50 | 20 | 4000 |
| Сектор(вырез) | 95,75 | 20 | -157 |
мм., 
мм. — координаты центра тяжести кругового сектора.
4. Определяем координаты центра тяжести всей фигуры:
мм.
мм.
5. По полученным координатам обозначаем центр тяжести всей фигуры на её чертеже (рисунок 20).
Задача для самостоятельного решения. Определить координаты центра тяжести плоской фигуры, указанной на рисунке 24. Первые 10 вариантов решают задачу для 1 фигуры, следующие (с 11 по 20) – для 2 фигуры, следующие (с 21 по 30) – для 3 фигуры.
Х
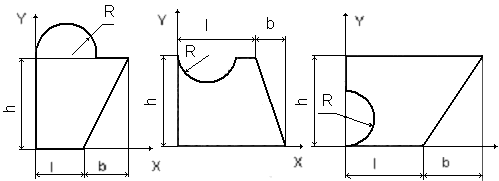
Рисунок 24. Сложные фигуры для задания 1.6 (пример1)
Таблица 6. Размеры элементов сложной фигуры для задания 1.6 (пример 1).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| R, мм | 10 | 20 | 15 | 25 | 30 | 28 | 24 | 22 | 18 | 16 |
| h, мм | 50 | 60 | 40 | 80 | 80 | 70 | 90 | 60 | 50 | 40 |
| l, мм | 60 | 50 | 50 | 60 | 60 | 80 | 70 | 80 | 80 | 60 |
| b, мм | 20 | 10 | 10 | 20 | 20 | 30 | 40 | 30 | 30 | 40 |
ПРИМЕР 2. Сложная фигура состоит из фасонных прокатных профилей (рисунок 25).
Рисунок 25. Сложная фигура, состоящая из прокатных профилей.
При решении этой задачи следует использовать сортамент на прокатные профили двутавры, швеллеры, уголки (таблицы 23, 24, 25). Решение задачи аналогичное решению предыдущей.
1. Разбивать заданную сложную фигуру на простые составные части не надо, так как она уже разбита на двутавр №24, швеллер №18, равнобокий уголок №9.
2. Определим по сортаментам на фасонные прокатные профили площади составных частей: площадь двутавра №24 
см 2 (таблица 23), площадь швеллера №18 
см 2 (таблица 24), площадь равнобокого уголка №9 
см 2 (таблица 25).
3. Выбираем систему координат, обозначаем положения центров тяжести составных частей и определяем их координаты в выбранной системе координат в сантиметрах:
см -координаты центра тяжести двутавра №24.
см., 
см- координаты центра тяжести швеллера №18.
см., 
см. — координаты центра тяжести равнобокого уголка №9.
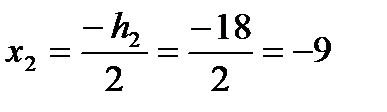
4. Определяем координаты центра тяжести всей фигуры по формулам:
см.
см.
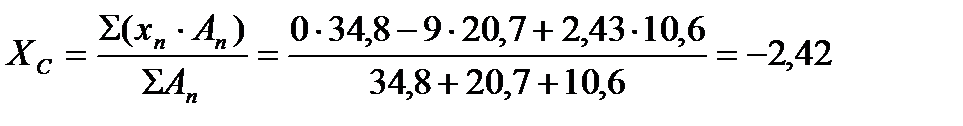
6. По полученным координатам обозначаем центр тяжести сложной фигуры на её чертеже (рисунок 25).
Задача для самостоятельного решения. Определить координаты центра тяжести фигуры, указанной на рисунке 26. Первые 10 вариантов выполняют решение для 1 фигуры, следующие (с 11 по 20) – для 2 фигуры, следующие (с 21 по 30) – для 3 фигуры.
.Рисунок 26. Сложные фигуры для задания 1.6 (пример 2)
Таблица 7. Номера профилей для задания 1.6. (пример 2)
Источник
Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
Источник
