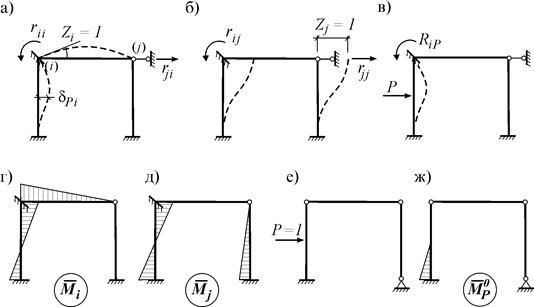
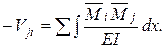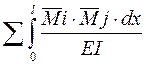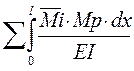Определение коэффициентов канонических уравнений. Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Статический способ основан на определении реакций во введенных связях основной системы из уравнений статики. Для этого необходимо вырезать отдельные узлы или части основной системы и составлять уравнения равновесия (статики). Если искомая реакция является реактивным моментом, то она определяется из условия равенства нулю момента в узле SM=0, если же она является реактивной силой, то определяется из уравнения проекции на ось (например, на ось x) в направлении этой реакции SX=0. Статический способ достаточно прост для использования, поэтому является основным способом определения коэффициентов системы канонических уравнений.
Докажем одну полезную теорему.
Теорема Релея. Реакция, возникающая в j-ой связи от перемещения i-ой связи на единицу, равна реакции i-ой связи от перемещения j-ой связи на единицу, т.е.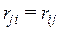 
.
Доказательство. Рассмотрим i-ое и j-ое единичные состояния основной системы некоторой рамы (рис. 11.3 а, б) и соответствующие эпюры моментов в этих состояниях (рис. 11.3 г, д).
Возможная работа сил j-ого единичного состояния (рис. 11.3 б) на перемещениях i-го состояния (рис. 11.3 а) равна
.
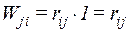
Работа сил i-го состояния на перемещениях j-го состояния будет
.
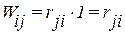
По теореме Бетти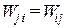 
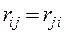
. Значит, равны и правые части, т.е. 
.
Эту теорему иногда называют теоремой о взаимности реакций. Она позволяет сократить объем вычислений побочных коэффициентов канонических уравнений.
Кинематический способ основан на определении коэффициентов канонических уравнений перемножением эпюр. Этот способ применяется при сложности определения коэффициентов статическим способом или для проверки результатов статического способа.
Для вывода формулы кинематического способа определим две возможные работы. Работа внешних сил j-го единичного состояния на перемещениях i-го состояния нам известна: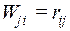 
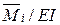
. А возможная работа внутренних сил j-го единичного состояния на деформации i-го состояния 
равна:
По принципу возможных перемещений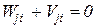 
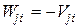
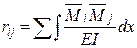
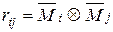
или 
. Отсюда получаем искомую формулу:
или 
.
Формула вычисления грузовых коэффициентов отличается от аналогичной формулы метода сил (дается без вывода):
или 
,
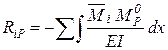
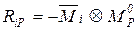
где 
– грузовая эпюра изгибающих моментов в любой статически определимой системе, полученной из заданной системы удалением лишних связей.
Дата добавления: 2015-06-17 ; просмотров: 1180 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Канонические уравнения метода сил.
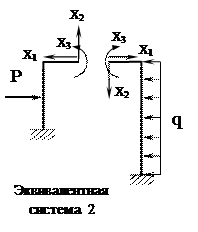
Основной системой называется статически определимая и геометрически неизменяемая система, полученная из заданной системы путем отбрасывания всех лишних связей ( за исключением абсолютно необходимых). Построение основной системы может быть произведено различными способами. Выбор основной системы является важным этапом расчета, т.к. от него зависит простота и точность расчета рамы.
Устранение каких-либо связей не изменяет внутренних усилий, возникающих в системе, и ее деформаций, если к ней прикладываются дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Поэтому, если к основной системе, кроме заданной нагрузки, приложить реакции устраненных связей, то полученная система и заданная система будут эквивалентны. Полученная таким образом система называется эквивалентной системой.
 |
 |
 |
 |
 |
В заданной системе в направлении имеющихся жестких связей ( в том числе и тех связей, которые отброшены при переходе к основной системе) перемещений быть не может. Поэтому в эквивалентной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно, реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям равнялись бы нулю. Таким образом, условие равенства эквивалентной и заданной систем математически сводится к удовлетворению системы n линейных уравнений:
 |
Эти уравнения являются теми дополнительными уравнениями деформаций (перемещений), которые позволяют раскрыть статическую неопределимость заданной системы. Данные уравнения называются каноническими уравнениями метода сил. Первое из этих уравнений выражает мысль о равенстве нулю перемещения в эквивалентной системе по направлению первой отброшенной связи (по направлению силы или момента Χ1), второе – по направлению второй отброшенной связи и т.д.
Число уравнений равно числу отброшенных связей, т.е. степени статической неопределимости заданной системы.
В системе канонических уравнений в качестве коэффициентов при неизвестных стоят перемещения основной системы, вызываемые единичными силами или моментами, действующими по направлениям отброшенных связей. Коэффициент δij представляет перемещение по направлению связи i , вызванное силой (моментом), равной единице, действующей по направлению связи j . Коэффициенты δij носят название единичных коэффициентов канонических уравнений. Коэффициент Δiр представляет перемещение по направлению связи i, вызванное действием заданной внешней нагрузки. Коэффициенты Δiр называются грузовыми коэффициентами или свободными членами канонических уравнений.
Коэффициенты δii называются главными коэффициентами, а коэффициенты δij – побочными. На основании теоремы о взаимности перемещений δij = δji .
Определяются коэффициенты канонических уравнений с помощью интегралов Мора по формулам :
δij = 
Δiр = 
т.к. рамы это конструкции, работающие преимущественно на изгиб, то в выражении интегралов Мора с соблюдением достаточной точности остаются только слагаемые, зависящие от изгибающих моментов.
Для подсчета коэффициентов вычерчиваются единичные эпюры Мi изгибающих моментов в основной системе, т.е. эпюры от действия Хi = 1. Отдельно строится грузовая эпюра Мр. Единичное перемещение δij вычисляется «перемножением» единичной эпюры Мi на единичную эпюру Мj , а грузовое перемещение – «перемножением» единичной эпюры Мi на грузовую эпюру М р по правилу Верещагина.
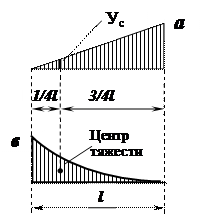
Правило Верещагина:Результат «перемножения» двух эпюр равен произведению площади Ω одной из них на ординату ус другой (обязательно прямолинейной) эпюры, взятую под центром тяжести площади первой эпюры. При перемножении ставится знак плюс, когда эпюра и ордината под центром ее тяжести, взятая из другой эпюры, имеют одинаковые знаки, и минус, — когда разные знаки. (Значения площадей и координаты центров тяжести приведены в приложении 1.)
Результат выполненного по правилу Верещагина перемножения эпюр для определения искомого перемещения следует разделить на величину EI.
ПРИМЕР
Ус = ⅔ ·в
Правилом Верещагина можно пользоваться в том случае, если одна из подынтегральных функций линейна, т.е. одна из «перемножаемых» эпюр прямолинейна, а другая может быть прямолинейной, ломаной или криволинейной.
ПРИМЕР
| |
Если эпюра моментов на одном участке меняется, т.е. не является непрерывной и образует две различных подынтегральных функции, то такой участок разбивается на два участка и «перемножение» эпюр производится уже по двум соответствующим участкам.
Если обе подынтегральные функции криволинейны на одном участке
длиной l , то для приближенного вычисленияинтеграла Мора можно пользоваться формулой Симпсона.( С помощью формулы Симпсона можно « перемножать» любые эпюры.)
 |
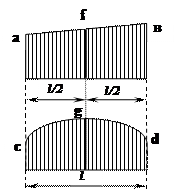l/6 · (a · c + 4 ·f·g + в · d)
Источник
Определение коэффициентов канонических уравнений
Коэффициенты при неизвестных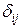 
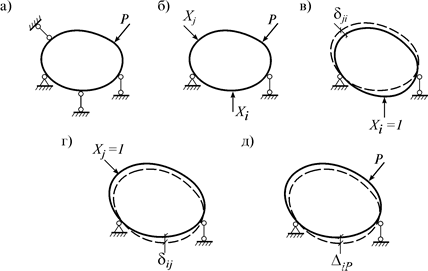
и грузовые коэффициенты DiP системы канонических уравнений – возможные перемещения от единичных сил и нагрузки. У них есть два индекса. Первый индекс i указывает на направление, а второй индекс j (или P) – на причину перемещения.
Методику вычисления этих коэффициентов рассмотрим на примере условной статически неопределимой системы (рис. 7.4 а) и ее основной системы (рис. 7.4 б).
Для определения коэффициентов 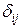рассмотрим два состояния ОС:
1) i-ое единичное состояние – воздействие силы Xi=1 (рис. 7.4 в);
2) j-ое единичное состояние – воздействие силы Xj=1 (рис. 7.4 г).
Если в этих состояниях возникают внутренние усилия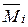 
, 
, 
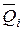
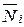
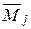
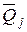
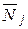
и 
, 
, 
, то возможная работа внутренних сил i-го состояния на деформациях j-го состояния будет:
–Vij=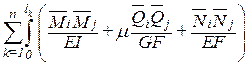 
dx.
С другой стороны, возможная работа внешних сил i-го состояния на перемещениях j-го состояния равна
По принципу возможных перемещений Wij=–Vij. Приравнивая их получаем формулу для вычисления коэффициентов при неизвестных:
dij=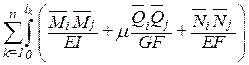 
dx .
Теорема Максвелла. Перемещение в i-ом направлении от единичной силы в j-ом направлении равна перемещению в j-ом направлении от единичной силы в i-ом направлении, т.е. dij=dji .
Доказательство. Возможную работу сил i-го единичного состояния (рис. 7.4 в) на перемещениях j-го состояния (рис. 7.4 г) мы уже знаем: Wij=dij. А возможная работа сил j-го состояния на перемещениях i-го состояния равна Wji=1×dji=dji. По теореме Бетти Wij=Wji. Следовательно, dij=dji .
Эта теорема позволяет уменьшать объем вычислений при нахождении боковых коэффициентов системы канонических уравнений.
Теперь выведем формулу вычисления грузовых коэффициентов.
Вначале определим возможную работу сил i-го единичного состояния (рис. 7.4 в) на перемещениях грузового состояния (рис. 7.4 д):
С другой стороны, возможная работа внутренних сил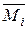 
, 
, 
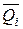
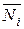
i-го единичного состояния на деформациях грузового состояния равна
–ViP=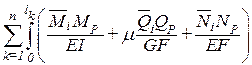 
dx.
По принципу возможных перемещений WiP= –ViP. Приравнивая их получим формулу вычисления грузовых коэффициентов: DiP=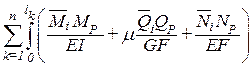 
dx.
Так как в рамах и балках перемещения определяются в основном изгибными деформациями, то коэффициенты канонических уравнений можно вычислять по сокращенным формулам:
= 
dx= 
,
= 
dx= 
,
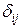
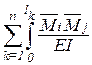
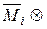
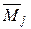
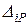
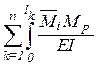
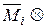
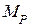
где знак 
используется для сокращения записи формулы вычисления интеграла Мора и означает условное «произведение» двух эпюр.
В о п р о с ы
1. В чем состоит отличие статически неопределимых систем от статически определимых систем?
2. Как определяется число лишних связей статически неопределимой системы?
3. Каким требованиям должна удовлетворять основная система?
4. В чем заключается физический смысл канонических уравнений метода сил?
5. Чем отличается вычисление коэффициентов при неизвестных от вычисления грузовых коэффициентов?
6. Какое преимущество дает использование теоремы Максвелла?
Источник
