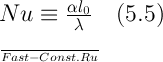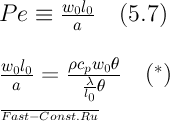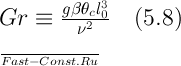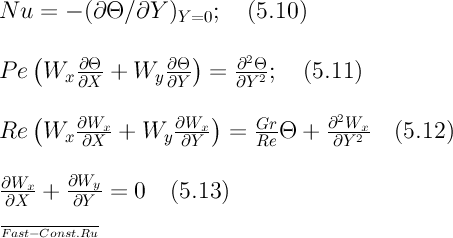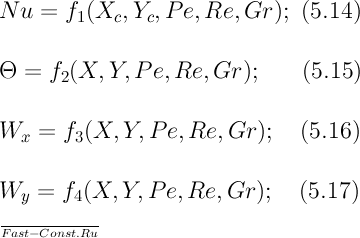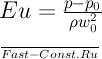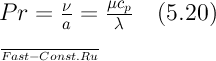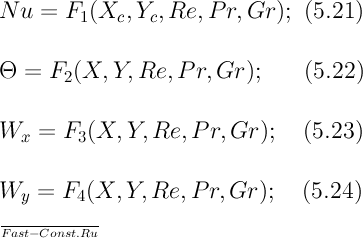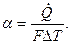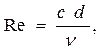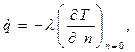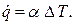Способы определения коэффициента теплоотдачи. Применение тории подобия к изучению конвективного теплообмена. Вывод определяемого критерия подобия Нуссельта.
Помимо безразмерных величин Θ, Wx, Wy и безразмерных координат, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин:
Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие гидродинамики или теплопередачи. Первый из этих безразмерных комплексов обозначают
и называют числом Нуссельта или безразмерным коэффициентом теплоотдачи. Число Нуссельта характеризует теплообмен на границе стенка — жидкость; это следует из уравнений (4.3) и (5.1). В задачах конвективного теплообмена число Nu обычно является искомой величиной, поскольку в него входит определяемая величина . Несмотря на внешнее сходство с числом Био, рассмотренным при изучении теплопроводности, число Нуссельта существенно отличается от него. В число Bi входит коэффициент теплопроводности твердого_тела; в число Nu — коэффициент теплопроводности жидкости. Кроме того, в число Био коэффициент теплоотдачи вводится как величина, заданная в условиях однозначности, мы же рассматриваем коэффициент теплоотдачи, входящий в Nu, как величину искомую. Безразмерный комплекс
называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости. Действительно, число Рейнольдса будет получено, если член уравнения движения, учитывающий инерционные силы, разделить на член, учитывающий в этом уравнении силы трения:
По существу такую же операцию мы проделали в § 5.2 при приведении уравнения движения к безразмерному виду. Число Рейнольдса является важной характеристикой как изотермического, так и неизотермического процессов течения жидкости. Третий безразмерный комплекс обозначают
и называют числом Пекле. Его можно преобразовать в выражение (*), здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель — теплоту, переносимую теплопроводностью. По существу мы получили ранее число Пекле путем деления конвективного члена уравнения на член, учитывающий перенос теплоты теплопроводностью. Безразмерный комплекс
называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей. Так как при выводе уравнения движения (4.18) было принято, что βθ=(ρ0–ρ)/ρ0, вместо Gr можно написать его более общую модификацию — число Архимеда:
В случае однородной среды при условии β=const число Архимеда идентично числу Gr. Используя введенные обозначения, систему безразмерных дифференциальных уравнений можно записать в следующем виде:
Система безразмерных дифференциальных уравнений и безразмерных условий однозначности представляет собой математическую формулировку задачи. Безразмерные величины Θ, Wx, Wy, X, Y, Nu, Re, Ре, Gr можно рассматривать как новые переменные. Их можно разделить на три группы:
независимые переменные — это безразмерные координаты X, Y; зависимые переменные — это Nu, Θ, Wx; Wy; они однозначно определяются значениями независимых переменных при определенных значениях величин, входящих в условия однозначности;
постоянные величины — это Ре, Re, Gr; они заданы условиями однозначности и для конкретной задачи являются постоянными [действительно, как следует из (5.6) — (5.8), числа Ре, Re и Gr состоят только из величин, входящих в условия задачи].
В результате можно написать:
Уравнения вида (5.14) — (5.17) называют уравнениями подобия. Здесь Хс, Yc — уравнение (5.14)—соответствуют поверхности теплоотдачи (стенки). Нахождение (или Nu) для точек пространства, не лежащих на поверхности стенки, не имеет смысла. В рассматриваемой задаче Yс=0. Если в уравнении движения учесть член (1/ρ)(∂p/∂x) то в результате приведения к безразмерной записи появился бы и член
Безразмерный комплекс (5.18) называют числом Эйлера. Это число характеризует соотношение сил давления и сил инерции. В уравнения конвективного теплообмена зависимая переменная Еu входит только под знаком производной. Следовательно, для рассматриваемой нами несжимаемой жидкости с постоянными физическими параметрами существенно не абсолютное значение давления, а его изменение (в случае сжимаемых течений нужно учитывать зависимость плотности от давления; в этом случае представляет интерес абсолютная величина давления). Поэтому число Эйлера обычно представляют в виде
где p0 — какое-либо фиксированное значение давления, например давление на входе в канал. Это давление может быть неизвестной величиной. Для многих процессов течения и теплоотдачи существен не только размер 0, но и некоторые другие характерные размеры. Например, при движении жидкости в прямой гладкой трубе характерными размерами являются диаметр и длина трубы; если труба изогнута, то дополнительным характерным размером является радиус кривизны трубы. При течении жидкости в шероховатых трубах представляют интерес размеры, оценивающие высоту неровностей и их концентрацию на поверхности теплообмена. Все необходимые размеры 0, 1, 2 и т. д. должны быть заданы в условиях задачи. В этом случае под знаком функции в уравнениях (5.14) — (5.17) должны быть величины L1=l1\l0; L2=l2\l0 Очевидно, внесение в этом случае под знак функции величин L1, L2, . , Ln является необходимым. Во всех случаях список безразмерных величин должен соответствовать математической формулировке задачи. Произвольное же исключение или введение под знак функции новых переменных безусловно недопустимо. Любая подобного рода операция должна быть обоснована. Очевидно, при неизменной математической формулировке задачи новые безразмерные величины могут быть получены соответствующим комбинированием старых безразмерных величин, однако при этом число переменных под знаком функции не должно измениться. Число Ре, полученное при приведении к безразмерному виду уравнения энергии, можно представить как произведение двух безразмерных переменных
Безразмерная величина Pr=v\a представляет собой новую переменную, называемую числом Прандтля. Число Прандтля целиком составлено из физических параметров, и поэтому и само является физическим параметром. Его можно записать и в виде
Числу Прандтля можно придать определенный физический смысл. Уравнение энергии (4.30)
и уравнение движения (4.28)
по записи аналогичны.
При a=v расчетные поля температур и скоростей будут подобны, если только аналогичны и условия однозначности. Условию a=v соответствует равенство Рr=1. Таким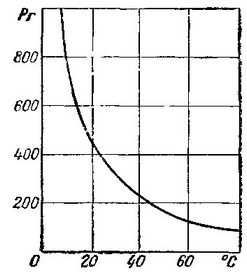 
образом, при определенных условиях числу Прандтля может быть придан смысл меры подобия полей температур и скоростей. Числа Рr капельных жидкостей сильно зависят от температуры, причем для большинства жидкостей эта зависимость в основном аналогична зависимости вязкости μ(t), так как теплоемкость ср и коэффициент теплопроводности λ зависят от температуры более слабо. Как правило, при увеличении температуры число Рr резко уменьшается(1).
Рис. 1. Изменение числа Прандтля трансформаторного масла в зависимости от температуры
Зависимость числа Рr воды от температуры на линии насыщения приведена на рис. 2. Значения числа Рr для воды при температурах от 0 до 180°С сильно уменьшаются с ростом температуры (от 13,7 до 1), что связано с резким уменьшением вязкости воды и ростом λ в этой области температур. Теплоемкость при этом очень мало зависит от температуры. При температурах от 130 до 310°С значения числа Рr для воды очень незначительно изменяются и близки к единице.
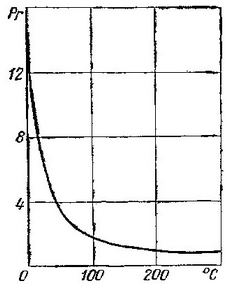
Рис. 2. Изменение числа Прандтля воды в зависимости от температуры в интервале температур от 0 до 300°С
Характер зависимости Рr от температуры резко изменяется только при давлениях и температурах, близких к критическим. Теплообмен в околокритической области будет рассмотрен особо. Число Рr газов практически не зависит ни от температуры, ни от давления и для данного газа является величиной постоянной, определяемой атомностью газа. В соответствии с кинетической теорией:
Для одноатомных газов 0,67;
Для двухатомных газов 0,72;
Для трёхатомных газов 0,8;
Для четырёх и более атомных газов 1.
Действительные значения числа Рr реальных газов несколько отличаются от указанных значений. Числа Рr тяжелых и щелочных жидких металлов, применяемых в качестве теплоносителей, изменяются в пределах Рr≈0,005÷0,05. Малые значения числа Рr жидких металлов объясняются высокой теплопроводностью последних. В зависимости от значения числа Рr жидкости делят на три группы: жидкости с числами Рr >1 (неметаллические капельные жидкости). Учитывая, что Pe=RePr, уравнения подобия (5.14)—(5.17) можно записать в виде
Исходя из уравнений (5.14) — (5.17) и (5.21) — (5.24), безразмерные переменные можно разделить на два вида:
определяемые—это числа, в которые входят искомые зависимые переменные; в рассматриваемом случае зависимыми являются , θ, ωх и wy, следовательно, определяемыми являются Nu, Θ, Wx и Wy;
определяющие — это числа, целиком составленные из независимых переменных и постоянных величин, входящих в условия однозначности; в рассматриваемом случае определяющими являются X, Y, Re, Рr (или Ре) и Gr.
Числа подобия, составленные из наперед заданных параметров (постоянных) математического описания процесса, называют также критериями подобия.
Дата добавления: 2018-05-02 ; просмотров: 954 ; Мы поможем в написании вашей работы!
Источник
Теплоотдача
7.1.1.Основной закон теплоотдачи
Понятие конвективного теплообмена охватывает процесс переноса теплоты конвекцией между твердыми поверхностями и омывающими их теплоносителями. Теплоносителем, как правило, является либо жидкость, либо газ. Однако в качестве теплоносителей могут использоваться двух- или трехфазные системы: газ – жидкость; газ – твердые частицы; газ – жидкость – твердые частицы.
В теплоносителе с неоднородным полем температур при вынужденном или естественном перемещении макроскопических элементов наряду с конвекцией происходит процесс переноса тепла теплопроводностью.
Совместный процесс конвекции и теплопроводности называют конвективным теплообменом.
Конвективный теплообмен протекает как внутри теплоносителя, так и на границах его соприкосновения с поверхностями обтекаемых тел.
Конвективный теплообмен между теплоносителем и поверхностью обтекаемого им тела называют теплоотдачей.
Обычно в инженерной практике исследуют теплоотдачу, конвективный же теплообмен внутри теплоносителя при этом не рассматривается.
Тепловой поток при теплоотдаче всегда направлен в сторону меньшей температуры. В процессе теплоотдачи плотность теплового потока, согласно закону Ньютона, прямо пропорциональна температурному напору между теплоносителем и поверхностью теплообмена, т.е.
(7.1)
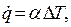
где α – коэффициент пропорциональности, называемый к о э ф ф и ц и е н-
т о м т е п л о о т д а ч и;
∆Т – температурный напор.
Здесь индексом m обозначена температура теплоносителя, индексом cm
– температура поверхности теплообмена (стенки).
Для произвольной поверхности при Tm > Tcm закон Ньютона запишется в виде:
. (7.2)
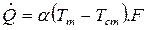
Значения F, Tm и Tcm в уравнении (6.2) не отражают условий теплообмена, влияющих на величину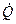 
. Здесь α не является физической постоянной, присущей данному теплоносителю, а зависит от множества факторов, формирующих картину течения около стенки. По этой причине простота уравнения (7.1) представляется кажущейся, и особенности его использования заключаются в сложности определения коэффициента теплоотдачи.
7.1.2. Факторы, влияющие на коэффициент теплоотдачи.
Величина коэффициента теплоотдачи характеризует интенсивность конвективного теплообмена на границе “теплоноситель-стенка”.
Численно коэффициент теплоотдачи равен тепловому потоку, приходящемуся на единицу поверхности при температурном напоре, равный единице, т.е.
Отсюда же следует и единица α – Вт/(м 2 × К).
Коэффициент теплоотдачи имеет весьма широкий диапазон численных значений, табл. 7.1.
| Особенности теплоотдачи |  . |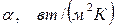
| Естественная конвекция газов | 6…40 |
| Вынужденное движение газов | 12…120 |
| Вынужденное движение пара в трубах | 110…2200 |
| Естественная конвекция воды | 110…1100 |
| Вынужденное движение воды | 500…11000 |
| Пузырьковое кипение воды | 8500…18000 |
| Конденсация водяного пара | 4500…22000 |
На величину коэффициента теплоотдачи влияют, прежде всего, теплофизические свойства теплоносителя, его фазовое состояние, вид движения (естественное или вынужденное) и режим течения теплоносителя. Различают ламинарный, переходный и турбулентный режимы течения.
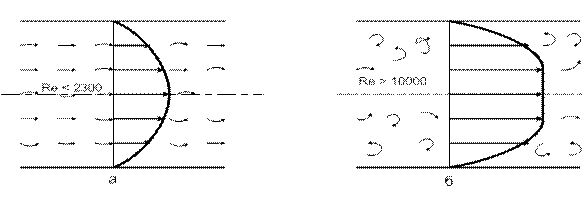
При ламинарном (слоистом) режиме макрочастицы жидкости движутся, не перемешиваясь, параллельно омываемым стенкам и траекториям других частиц. В силу внутреннего трения скорость теплоносителя переменна по сечению нормальному к поверхности. Так, для канала круглого сечения эпюра скорости имеет параболическую форму, рис.7.1, а Перенос тепла при ламинарном режиме движения происходит в осноном за счет теплопроводности теплоносителя и естественной конвекции.
При турбулентном режиме макрочастицы перемещаются по сложным траекториям, не совпадающим с общим направлением потока. Их движение неупорядоченное, хаотичное. Эпюра скорости имеет вид усеченной параболы, (см. рис. 7.1, б). Теплоотдача при турбулентном режиме течения теплоносителя отличается несравненно большей интенсивностью, чем при ламинарном режиме
Как при ламинарном, так и при турбулентном режимах движения скорость теплоносителя непосредственно на стенке равна нулю, а с увели -чением расстояния по нормали от стенки она возрастает.
Слой теплоносителя около поверхности тела, где скорость изменяется от нуля до величины, примерно равной 0,9 скорости невозмущенного потока, называют г и д р о д и н а м и ч е с к и м пограничным слоем и обозначают буквой δд , рис.7.2.
Кроме того, необходимо отметить, что в турбулентном пограничном слое непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или л а м и н а р н ы м п о д с л о е м и обозначают δл (см. рис. 7.2, б).
Если температуры стенки и теплоносителя не одинаковы, то вблизи стенки образуется тепловой пограничный слой δт (см. рис.7.2, в). В нем температура изменяется от Tcm до ≈ Tm , т.е. все изменение температуры происходит в сравнительно тонком слое, непосредственно прилегающем к поверхности теплоотдачи. Значения толщин δд и δт в общем случае не равны, соотношение между ними зависит от рода жидкости. Однако изменения в δд приводят к изменениям δт. С увеличением скорости теплоносителя значения толщин δд , δт и δл уменьшаются.
При вынужденной конвекции режим течения оценивают по безразмерному комплексу, называемому критерием Рейнольдса. Для цилиндрического канала критерий Рейнольдса имеет вид:
где c — скорость течения теплоносителя,;
d — диаметр канала,;
ν — коэффициент кинематической вязкости,.
Течение теплоносителя в трубах принято считать ламинарным до
Re Re 10000 течение турбулентное.
Для того, чтобы качественно оценить влияние режима течения теплоносителя на коэффициент теплоотдачи, запишем уравнение теплоотдачи в дифференциальной форме.
Для слоя теплоносителя непосредственно на поверхности теплообмена по закону Фурье следует:
где n – нормаль к поверхности тела,.
С другой стороны, согласно закону Ньютона,
Приравнивая правые части этих уравнений, получим:
(7.3)
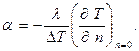
Уравнение (7.3) выражает условия теплоотдачи на границе “твердая стенка – теплоноситель”.
Чем больше скорость движения теплоносителя, тем меньше толщина пограничного слоя, тем больше градиент температуры и, следовательно, больше коэффициент теплоотдачи. Через толщину пограничного слоя на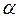 
влияют форма и размер поверхности теплообмена.
Величина коэффициента теплоотдачи зависит от физических свойств теплоносителя.С увеличением плотностиρ, теплопроводности λ, теплоем-кости cpи уменьшением вязкости ν коэффициент теплоотдачи возрастает.
Влияние температур Tm и Tcm на 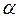сказывается через их воздействие на физические свойства теплоносителя.
Таким образом, в самом общем виде коэффициент теплоотдачи является функцией многих факторов:
где X – характер движения теплоносителя;
Ф – форма поверхности теплообмена;
l – характерный геометрический размер;
c – скорость движения теплоносителя.
Для определения коэффициента теплоотдачи в зависимости от поста-
новки задачи могут использоваться следующие методы: экспериментальный,
аналитический и метод теплового подобия.
Чисто экспериментальный метод определения коэффициента теплоотдачи весьма прост и достоверен, так как требует опытного измерения
только трех величин: 
, Tm и Tcm. Отсюда
.
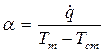
Этот метод широко используется при исследовании влияния различных факторов на интенсивность теплоотдачи в функционирующих теплообменных установках. Однако экспериментальный метод имеет существенный недостаток, состоящий в том, что полученное значение α не может быть рекомендовано для использования при расчетах устройства, характеристики которого хотя бы незначительно отличаются от характеристик опытной установки.
Аналитические методы основаны на теории пограничного слоя. Сущность этих методов состоит в составлении замкнутой системы дифференциальных уравнений, описывающих процесс конвективного теплообмена в движущемся теплоносителе и последующем решении этой системы. Дифференциальные уравнения, описывающие конвективный теплообмен, устанавливают самую общую связь между величинами, характерными для этого процесса. Следовательно, эти дифференциальные уравнения являются математической моделью целого класса процессов теплообмена. Для получения частного решения эти уравнения дополняются условиями однозначности.
В большинстве случаев, из-за сложности математического описания профиля скорости в пограничном слое, решения, удовлетворяющие дифференциальным уравнениям и условиям однозначности, весьма трудоемки.
Следовательно, если недостатком экспериментального метода определения α является невозможность распространения результатов опытов на другие условия теплообмена, отличающиеся от изученного, то недостатком аналитического метода является невозможность перейти от класса явлений конвективного теплообмена, характеризующегося дифференциальными уравнениями, к единичному, конкретному явлению. Каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.
В настоящее время для определения коэффициента теплоотдачи в основном используется метод теплового подобия, который объединяет в себе положительные стороны экспериментального и аналитического методов.
Источник
