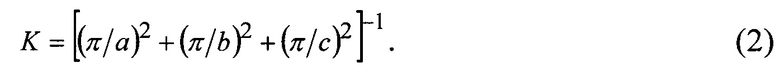Способы определения коэффициента диффузии

СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ ЖИДКОСТИ В КАПИЛЛЯРНО-ПОРИСТОМ ТЕЛЕ ПРИ ВОЗДЕЙСТВИИ УЛЬТРАЗВУКОМ Российский патент 2018 года по МПК G01N15/08

Описание патента на изобретение RU2649082C1

Изобретение относится к теоретической теплотехнике и может быть использовано для определения коэффициента диффузии D жидкости в материалах, имеющих капиллярно-пористую структуру, при воздействии ультразвуком.

В капиллярно-пористых телах процесс тепломассообмена в ульятразвуковом поле, в значительной степени усложняется в условиях изменения влагосодержания в поровом пространстве. При моделировании тепловлажностного состояния капиллярно-пористого тела учет особенностей материала, таких как размер пор, их форма, расположение выполняют интегрально через определение эффективных свойств.

Известен способ (см. патент РФ №2212027 — Опубл. 10.09.2003.), включающий нанесение пленки диффундирующего элемента на поверхность металла, стимулирующее диффузию воздействия, определение изменения концентрации элемента в металле и расчет коэффициента диффузии элемента по концентрационной зависимости.

Недостатком данного способа является невозможность определения коэффициента диффузии у капиллярно-пористых тел, так же не учитывается возможность воздействия ультразвуком.

Известен способ (см. патент РФ №2398214 — Опубл. 27.08.2010.), основанный на анализе цифрового изображения плоскопараллельной вертикальной ячейки с неоднородным распределением концентрации, позволяющий определить коэффициент диффузии окрашенных растворов различных веществ.

Недостатком данного способа является неточность определения коэффициента диффузии, так как не учитывается пористое внутреннее строение тел, невозможность определения коэффициента диффузии при воздействии ультразвуком.

Наиболее близким по техническому решению является способ регулярного теплового режима [1]. Этот способ служит основой для достаточно простого определения теплофизических свойств материалов и коэффициентов теплоотдачи. Основная закономерность регулярного режима состоит в том, что при теплообмене в регулярном режиме натуральный логарифм избыточной температуры связан со временем линейной зависимостью. Угол наклона прямой характеризуется коэффициентом m — темпом регулярного режима.

Недостатком данного способа является определение темпа регулярного режима лишь при теплопроводности, так же невозможность определения коэффициента диффузии при воздействии ультразвуком.

Общим признаком прототипа и предлагаемого решения является нахождение коэффициента m — темпа регулярного режима путем построения зависимости натурального логарифма избыточных измеряемых величин от времени, а также нахождения K — коэффициента формы тела.

Техническим результатом предлагаемого способа является определение коэффициента диффузии капиллярно-пористого тела при воздействии ультразвуком.

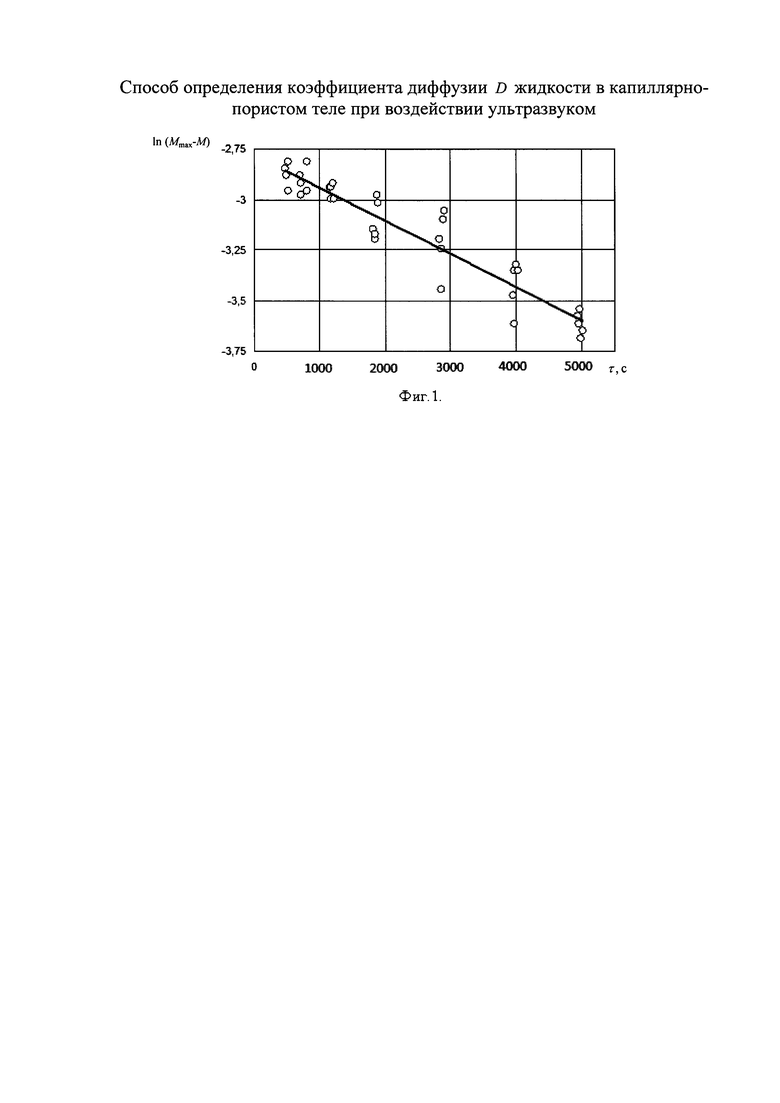
Сущность способа поясняется фиг. 1, где приведены результаты определения темпа регулярного режима влагопереноса, где ο — экспериментальные данные; сплошная линия — линейная аппроксимирующая зависимость.

Предлагаемый способ заключается в том, что коэффициент диффузии D жидкости в капиллярно-пористом теле при воздействии ультразвуком в рассматриваемых условиях является параметром-аналогом коэффициента температуропроводности. Коэффициент диффузии D жидкости в капиллярно-пористом теле при воздействии ультразвуком определяется экспериментально на основе аналогии с методом регулярного теплового режима по выражению:

где K — коэффициент формы тела; m — темп регулярного режима влагопереноса.

Коэффициент формы тела K определяется аналогично методу регулярного теплового режима. Так, например, для тела в виде прямоугольного параллелепипеда размерами axbxc имеем [1]:

Для отыскания темпа регулярного режима влагопереноса m осушенное капиллярно-пористое тело погружают в воду, воздействуют на тело ультразвуком и определяют изменение с течением времени его массы, которая однозначно связана со средним влагосодержанием. По результатам эксперимента строят зависимость натурального логарифма избыточной массы (разности максимальной массы тела после его длительного пребывания в воде и массы в текущий момент времени, отсчитываемый от начала погружения) от времени. На полученной зависимости выделяют стадию регулярного режима влагопереноса, характеризуемую тем, что опытные точки на графике группируются около прямой линии. Тангенс угла наклона этой прямой к оси абсцисс на графике численно равен значению темпа регулярного режима влагопереноса m. Далее по формуле (1) рассчитывают коэффициент диффузии D при воздействии ультразвуком.

По изложенной методике определен коэффициент диффузии D при воздействии ультразвуком жидкости для красного строительного кирпича. Результаты эксперимента с пятью экземплярами кирпича для стадии регулярного режима влагопереноса приведены на фиг. 1. При обработке полученных результатов были определены значения K=3,191⋅10 -4 м 2 ; m=1,2⋅10 -4 с -1 ; D=3,84⋅10 -8 м 2 /с. Относительная погрешность определения коэффициента диффузии, приведенная к доверительной вероятности 0,95, составляет ±5%.

Информационный материал, используемый при составлении описания:

1. Теплопередача — Исаченко В.П., Осипова В.А., Сукомел А.С. Учебник для вузов, изд. 3-е, перераб. и доп. — М., «Энергия», 1975 г. — 488 с.

Похожие патенты RU2649082C1

название	год	авторы	номер документа
СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ ЖИДКОСТИ В КАПИЛЛЯРНО-ПОРИСТОМ ТЕЛЕ	2011	Ковальногов Владислав Николаевич Ковальногов Николай Николаевич Павловичева Тамара Владимировна	RU2469292C1
Способ определения запасов природного газа глубокозалегающей газоконденсатной залежи, разрабатываемой в режиме истощения	1987	Алиев Акиф Исмайлович Караш Оскар Эдуардович Салаев Эльдар Субхи Оглы Эйдельман Лев Романович Али-Заде Нина Васильевна	SU1553656A1
СПОСОБ ОПРЕДЕЛЕНИЯ ЛЕТУЧЕСТИ И ТЕПЛОТЫ ИСПАРЕНИЯ СМЕСИ ЖИДКИХ ВЕЩЕСТВ	2012	Дроздова Валентина Владимировна Полякова Галина Юрьевна Дымнич Сергей Анатольевич Лоскутов Анатолий Юрьевич Кухоткин Сергей Владимирович Бойко Андрей Юрьевич Повалихин Анатолий Павлович Фоменко Павел Викторович	RU2488811C1
СПОСОБ ОПРЕДЕЛЕНИЯ ЗАПАСОВ ПРИРОДНОГО ГАЗА ГАЗОКОНДЕНСАТНОЙ ЗАЛЕЖИ	1992	Зильберман Владимир Иосифович[Ua] Волохов Владимир Яковлевич[Ua] Воронин Вячеслав Иванович[Ua] Винник Василий Матвеевич[Ua]	RU2067162C1
СПОСОБ ОПРЕДЕЛЕНИЯ СРЕДНЕЙ ПЛОТНОСТИ СВЯЗАННОЙ ЖИДКОСТИ КОЛЛОИДНЫХ И КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛ	2008	Афанасьев Алексей Егорович Ефремов Алексей Сергеевич	RU2380683C1
СПОСОБ ОБРАБОТКИ ИЗДЕЛИЙ ИЗ ТВЕРДОГО СПЛАВА	1993	Коршунов Анатолий Борисович Шемаев Борис Владимирович Шорин Анатолий Михайлович Пикунов Дмитрий Валентинович Щуркова Валентина Викторовна Миркин Лев Иосифович	RU2057619C1
СПОСОБ ОПРЕДЕЛЕНИЯ ЭНЕРГИИ АКТИВАЦИИ ПРОЦЕССА ДЕСОРБЦИИ	2011	Ферапонтов Юрий Анатольевич Гладышев Николай Федорович Гладышева Тамара Викторовна Ферапонтова Людмила Леонидовна Козадаев Леонид Эдуардович Путин Борис Викторович Путин Сергей Борисович	RU2469299C1
СПОСОБ ОПРЕДЕЛЕНИЯ ЭНЕРГИИ АКТИВАЦИИ ФАЗОВЫХ ПРЕВРАЩЕНИЙ ПРИ РАСПАДЕ МАРТЕНСИТА В СТАЛИ	2014	Ким Владимир Алексеевич Белова Инна Валерьевна	RU2574950C1
СПОСОБ И УСТРОЙСТВО ДЛЯ РАЗДЕЛЕНИЯ СМЕСИ ГАЗОВ ПО МОЛЕКУЛЯРНОЙ МАССЕ	2018	Якунчиков Артём Николаевич Редьков Алексей Викторович Косьянчук Василий Викторович	RU2708046C1
СПОСОБ ИДЕНТИФИКАЦИИ ПРОМЕЖУТОЧНЫХ ФАЗ В МОНОКРИСТАЛЛАХ СИЛИКАТОВ	2011	Петров Владимир Семенович Смирнов Игорь Сергеевич Яковлев Олег Иванович Слюта Евгений Николаевич Васильевский Владимир Викторович Монахов Иван Сергеевич Прокофьева Таисия Валерьевна Агафонов Антон Васильевич	RU2470288C1

Иллюстрации к изобретению RU 2 649 082 C1

Реферат патента 2018 года СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ ЖИДКОСТИ В КАПИЛЛЯРНО-ПОРИСТОМ ТЕЛЕ ПРИ ВОЗДЕЙСТВИИ УЛЬТРАЗВУКОМ

Изобретение относится к теоретической теплотехнике. Способ определения коэффициента диффузии жидкости в капиллярно-пористом теле, включающий погружение в воду капиллярно-пористого тела и определение изменения с течением времени его массы, отличающийся тем, что на тело воздействуют ультразвуком, по результатам эксперимента строят зависимость натурального логарифма избыточной массы от времени, на полученной зависимости выделяют стадию регулярного режима влагопереноса, характеризуемую тем, что опытные точки на графике сгруппированы около прямой линии, а тангенс угла наклона этой прямой к оси абсцисс на графике численно равен значению темпа регулярного режима влагопереноса, затем коэффициент диффузии жидкости в капиллярно-пористом теле определяют по формуле: D=Km, где K — коэффициент формы тела; m — темп регулярного режима влагопереноса. Технический результат заключается в обеспечении возможности определения коэффициента диффузии при воздействии ультразвуком. 1 ил.

Формула изобретения RU 2 649 082 C1

Способ определения коэффициента диффузии жидкости в капиллярно-пористом теле, включающий погружение в воду капиллярно-пористого тела и определение изменения с течением времени его массы, отличающийся тем, что на тело воздействуют ультразвуком, по результатам эксперимента строят зависимость натурального логарифма избыточной массы от времени, на полученной зависимости выделяют стадию регулярного режима влагопереноса, характеризуемую тем, что опытные точки на графике сгруппированы около прямой линии, а тангенс угла наклона этой прямой к оси абсцисс на графике численно равен значению темпа регулярного режима влагопереноса, затем коэффициент диффузии жидкости в капиллярно-пористом теле определяют по формуле:

Источник

Способы определения коэффициента диффузии

Экспериментальные исследования диффузии начались еще в прошлом столетии [147], к настоящему времени разработано достаточно надежных методов для определения коэффициентов молекулярной диффузии растворенных газов в жидкостях. Ряд из них основан на стационарной диффузии, и при выводе расчетного уравнения используется первый закон Фика. Другие протекают в нестационарных условиях с использованием второго закона Фика. Наиболее представительными являются методы, основанные на абсорбции газа при ламинарном режиме движения жидкости.

Метод ламинарной цилиндрической струи

Метод ламинарной цилиндрической струи широко применялся исследователями [6, 12, 22, 52, 53, 62, 72, 75, 79, 84, 85, 88, 87, 146, 147, 151, 167, 204, 205, 232, 233, 255, 257, 261, 265, 268, 284] для определения коэффициентов молекулярной диффузии газов в различных жидкостях. Метод основан на поглощении газа ламинарно-движущейся вертикальной цилиндрической струей жидкости. Схема установки показана на рис. 1.2.1.

Исследуемый газ из баллона 1 проходит через сатуратор 2, где насыщается парами растворителя. Далее насыщенный газ подогревается или охлаждается в теплообменнике 3 до заданной температуры и через расходомер 4 подается в диффузионную ячейку 5. Исследуемая жидкость (растворитель), предварительно дегазированная, поступает в диффузионную ячейку 5 к соплу 12 из напорного резервуара 8 через теплообменник 9. Из сопла 12 струя выходит строго цилиндрической формы, что достигается конструкцией выходного отверстия сопла и длиной струи, и поступает в приемную трубку 13. Сопла, которые представляют собой либо калиброванные капилляры, либо тонкие пластинки с отверстием, могут иметь различный диаметр, что связано с физическими свойствами растворителя, и подбираются опытным путем. Приемная трубка имеет внутренний диаметр несколько больший, чем диаметр струи. Обычно диаметр струи составляет около 1 10 –3 –1,5 10 –3 м, а ее длина – от 20 10 –3 до 30 10 –3 м. Уровень жидкости в приемной трубке, препятствующий прорыву газа из ячейки, регулируется подвижным гидрозатвором 7, который перемещается с помощью винта 11. Расход жидкости определяется объемным методом с помощью мерного стакана 6 либо калиброванным ротаметром. Количество поглощенного газа определяют мыльно-пленочным расходомером 4. С конструкцией такого расходомера можно ознакомиться в [11].

Перед началом эксперимента диффузионную ячейку 5 термостатируют и продувают исследуемым газом. После продувки в ячейку подается жидкость и производятся измерения расходов газа и жидкости. Длина струи тщательно измеряется катетометром. Температура жидкости и газа в ячейке 5 поддерживается постоянной в течение времени опыта при помощи ультратермостата 10 и теплообменников 3, 9.

Согласно [11, 147], большинство авторов обрабатывали данные своих измерений, допуская, что сопротивление на поверхности контакта фаз отсутствует и на поверхности струи мгновенно устанавливается равновесие.

Коэффициент молекулярной диффузии определяется по уравнению

см 2 /с, (1.2.1)

где Н – длина струи.

Значения равновесной концентрации берутся по справочникам в зависимости от температуры и давления либо рассчитываются по данным [119].

Метод ламинарной струи прост как в конструктивном исполнении, так и в проведении эксперимента. Время опыта относительно мало, что исключает адсорбцию поверхностно-активных веществ поверхностью жидкостной струи. Вышеперечисленные достоинства сделали этот метод широко распространенным и дающим достаточно точные значения D_АВ.

К недостаткам этого метода можно отнести то, что требуется относительно большое количество жидкости для проведения эксперимента, а также необходимость знать равновесную концентрацию. Если эти данные отсутствуют, то требуются дополнительные исследования по растворимости для данной газожидкостной системы.

Метод кольцевой ламинарной струи

Метод определения коэффициентов молекулярной диффузии газов в жидкостях при помощи кольцевой струи был разработан Бердом и Дэвидсоном [53] и отличается лишь формой поверхности струи жидкости, которая поглощает газ. Устройство для получения кольцевых струй, их динамика подробно описаны в [52].

Определение молекулярной диффузии данным методом производилось на установке, представленной на рис. 1.2.2 [53].

Подготовленная жидкость из резервуара 1 подается в устройство 2, предназначенное для образования кольцевой ламинарной струи, и, вытекая из него через кольцевое отверстие в нижней части (диаметр кольца по оси 12,41 10 –3 м, ширина 0,29 10 –3 м) устройства, образует сходящуюся кольцевую струю 3, вершина которой обтекает цилиндрическую трубку 4 по наружному диаметру. Далее жидкость стекает по трубке в бачок 5. Газ, предварительно насыщенный парами жидкости в сатураторе 10, подается через мыльно-пленочный расходомер 6 к устройству 2, в центральной части которого располагается вертикальная трубка для прохода газа внутрь кольцевой струи. Непрореагировавший газ через верхнюю часть трубки 4 проходит через бачок 5, не вступая в контакт с жидкостью, и поступает в мыльно-пленочный расходомер 7.

Таким образом, поверхность контакта газа с жидкостью ограничивается внутренней поверхностью кольцевой струи. Коэффициент молекулярной диффузии определяется из формулы:

, (1.2.2)

где – эффективная скорость (см. работу [52]); V – внутренний объем кольцевой струи.

Эффективная скорость определяется по формуле

, (1.2.3)

где U₀ – скорость истечения жидкости из отверстия; – расстояние от основания струи до отверстия.

Широкого распространения этот метод не получил ввиду сложности определения внутреннего объема струи по сравнению с цилиндрическими струями.

Рис. 1.2.1. Схема установки по методу ламинарной цилиндрической струи

Рис. 1.2.2. Схема установки по методу кольцевой ламинарной струи

Метод орошаемой стенки

Принципиальное отличие данного метода от предыдущих заключается лишь в конструкции диффузионной ячейки, представляющей собой колонну, в которой жидкость под действием силы тяжести стекает по поверхности трубки (в одних колоннах по внутренней [92], в других – по наружной [252]) или стержня.

На рис. 1.2.3 показана ячейка с орошаемой внутренней поверхностью трубки [92]. Исследуемая жидкость подается в колонну через патрубок, соединенный с наружным сосудом 1, и поднимается к верхней части орошаемой колонки 2. Внутри колонки 2 расположена трубка 3 для подачи газа, которая вместе с отводной частью 4 образует щель для подачи газа к орошаемой колонке. Верхняя часть колонки с отводной частью образует щель порядка 0,4 10 –3 м для создания пленки. Таким образом, жидкость стекает по внутренней стенке орошаемой колонки и поглощает подаваемый во внутреннюю трубку 3 снизу газ. Для предотвращения прорыва газа в орошаемой колонке поддерживается постоянный уровень жидкости. Высота орошаемой части колонки тщательно замеряется (размер h на рис. 1.2.3).

Рис. 1.2.3. Схема диффузионной ячейки с внутренней
орошаемой стенкой [70]

На рис. 1.2.4 показана диффузионная ячейка с орошаемой наружной стенкой, использованная Робертсом и Данквертсом [11].

Жидкость поднимается по внутренней части вертикальной трубки 1, а затем через кольцевую щель шириной 0,4 10 –3 м поступает на наружную поверхность трубки 1 диаметром 19 10 –3 м, по которой она стекает в виде пленки сверху вниз. Вывод жидкой пленки осуществляется через три вертикальных канала в полиэтиленовой втулке 3. Длину пленки можно изменять, перемещая вверх или вниз по трубе втулку и всю связанную с ней часть установки. Максимальная высота пленки в работе [11] составляла 0,25 м . Трубка поддерживалась в вертикальном положении с помощью специальных устройств. Расход жидкости изменялся от 2 до 8 см 3 /с. Коэффициент молекулярной диффузии определяли из уравнения

см 2 /c, (1.2.4)

где d – диаметр цилиндрической поверхности пленки; v – скорость движения пленки жидкости; h – высота пленки жидкости.

Рис. 1.2.4. Схема диффузионной ячейки с наружной
орошаемой стенкой [11]:
1 – вертикальная трубка; 2 – пленкообразующая насадка;
3 – полиэтиленовая втулка; 4 – теплообменник; 5 – опорная плита; 6 – крепление вертикальной трубки; 7 – регулировочный винт

Использование диффузионных ячеек с орошаемой стенкой, подобных вышеописанным, предполагает возможность возникновения концевых эффектов, волнообразования и застойных зон пленки. Концевые эффекты возникают в результате перераспределения скорости поверхности пленки между выходом пленки из распределительной щели и ее основной частью. Возникающую при этом ошибку уменьшают при конструировании ячеек. В работе Робертса и Данквертса ошибка от концевых эффектов составляла около 1 % [11].

Применение диффузионных ячеек с орошаемой стенкой ограничено и тем, что поверхность пленки не является гладкой, а покрыта рябью даже при низких скоростях потока, что приводит к искажению геометрических размеров пленки. Эммерт и Пигфорд [92] предложили использовать этот метод с помощью добавления поверхностно-активных веществ. Однако влияние этих веществ на молекулярную диффузию к настоящему времени не изучено.

Метод орошаемой сферы

В [84] был предложен метод орошаемой сферы, который является модификацией ячейки с орошаемой стенкой. Диффузионная ячейка с орошаемой сферой показана на рис. 1.2.5. Дегазированная жидкость из резервуара подается к распределителю 1, расположенному в верхней части ячейки. Из распределителя жидкость пленкой стекает по сфере 2, стержню 3 и покидает ячейку через приемную трубку 4. Прорыву газа из ячейки препятствует гидравлический затвор. Давление в ячейке измеряется дифманометром и не превышает 2 см вод. ст. (в СИ: 1 см вод. ст. = 98,07 Па) выше атмосферного. Сфера диаметром 3,78 10 –2 м крепится на вертикальном стержне из нержавеющей стали в 3 10 –3 м от выпускной щели. Пруток крепится верхним концом по центру распределителя, а нижним концом входит в приемную трубку 4. Расстояние 3 10 –3 м между щелью и верхней точкой сферы обеспечивает стекание жидкости по сфере без волнообразования на поверхности пленки. Уменьшение расстояния ведет к разбрызгиванию жидкости вокруг сферы уже при средних скоростях потока. Длина прутка составляет 1,5 10 –2 м. Экспериментально было установлено, что при длине прутка менее 2 10 –2 м скорость абсорбции постоянна. Когда же длина прутка больше 2 10 –2 м, вследствие волнообразования концевые явления становятся значительными, что приводит к повышению скорости абсорбции в этом месте.

Коэффициент молекулярной диффузии определяется из уравнения абсорбции:

см 2 /с, (1.2.5)

где S – радиус сферы, см.

Метод орошаемой сферы был применен для газов с умеренной растворимостью в жидкостях. По мнению авторов [84], он неприменим для газов, обладающих высокой растворимостью в жидкостях, из-за влияния на абсорбцию нагрева и концентрации растворенного газа. Метод орошаемой сферы является достаточно простым и сравнительно быстрым по проведению, что исключает влияние конвекции жидкости. Значения коэффициентов молекулярной диффузии, определенные методом орошаемой сферы, дают погрешность ± 5 %. При особой тщательности проведения эксперимента могут быть получены данные с точностью ± 1 % [84].

Рис. 1.2.5. Ячейка с орошаемой сферой [84]

Метод ячейки с диафрагмой

Рядом исследователей [107, 202, 213, 226, 251, 253, 268, 269] использовался метод определения коэффициента молекулярной диффузии газов и жидкостей в жидкостях в ячейке с диафрагмой.

Ячейка с диафрагмой (рис. 1.2.6) представляет собой сосуд 1, разделенный пополам горизонтальной диафрагмой 2, изготовленной из пористых стекла или металла. Размеры пор диска диафрагмы составляют 3–5 мкм. По обеим сторонам диска установлены магнитные мешалки 3. Диаметр диска составляет около 50 10 –3 м при толщине диафрагмы 5 10 –3 м. Газ диффундирует через поры из раствора с большей концентрацией в менее концентрированный. Диффузия через диафрагму протекает в стационарных условиях, т. к. раствор по обе стороны диафрагмы интенсивно перемешивается и можно считать концентрации в каждом из объемов постоянными в любой из точек данного объема.

Перемешивание при скорости вращения мешалки более 1 с –1 на диффузию не влияет [147]. Поскольку нельзя измерить величину поперечного сечения пор диафрагмы и их длину, необходимо каждую ячейку калибровать, чтобы определить постоянную ячейки b. Для этого используют раствор с известным коэффициентом диффузии. Так, например, для водных растворов наиболее часто применяют водный раствор KCl, т. к. для этого раствора известна зависимость коэффициента молекулярной диффузии от концентрации. Постоянная ячейки является функцией не только концентрации, но и вязкости раствора. Поэтому постоянную ячейки необходимо определять по жидкости, имеющей ту же вязкость, что и у исследуемая.

Рис. 1.2.6. Ячейка с диафрагмой:
1 – корпус; 2 – диафрагма; 3 – магнитные мешалки,
4 – вращающийся магнит; 5 – кран;
6 – газоподводящая трубка

Коэффициент молекулярной диффузии определяется по уравнению

, (1.2.6)

где С₁, С₃ – начальные концентрации растворов с высокой и низкой концентрацией соответственно; С₂, С₄ – конечные концентрации растворов с высокой и низкой концентрацией соответственно; t – время эксперимента.

Необходимость калибровки каждой ячейки, а также подбор жидкости для калибровки усложняют применение данного метода для определения коэффициентов молекулярной диффузии и вводят дополнительную погрешность в его значение. Также не изучено влияние поверхности пор на диффузию молекул газа и жидкости.

В [269] ошибка эксперимента по методу ячейки с диафрагмой для системы оксид углерода(IV)–вода составила ± 10 %.

Метод абсорбции в ячейке с капилляром

Впервые метод абсорбции с капилляром применял Стефан с целью продемонстрировать применимость закона Фика для диффузии газов в жидкостях. Метод предусматривает проведение диффузионного процесса в тонкой (порядка 1 10 –5 м) капиллярной трубке, что позволяет предотвратить конвективное перемешивание жидкости в течение эксперимента.

Эксперимент Стефана (рис. 1.2.7) сводится к следующему: капилляр 1 продувается исследуемым газом и помещается одним концом в жидкость 2. Часть жидкости поднимается в трубку за счет капиллярного эффекта и образовывает столбик жидкости 3 длиной l, через который и осуществляется диффузия. При растворении газа столбик жидкости перемещается в сторону газовой фазы. Зная точно объем капилляра и длину перемещения l, можно определить коэффициент молекулярной диффузии:

см 2 /с, (1.2.7)

где V – объем поглощенного газа; С * – растворимость газа при данных Р и Т; F – поверхность контакта фаз;
– время процесса диффузии.

В экспериментальной установке Стефана имеется ряд недостатков, которые принимались во внимание более поздними исследователями, применившими данный метод.

Рингбом [147] – один из первых, кто его усовершенствовал и использовал для измерения коэффициентов молекулярной диффузии СО₂ в воду. Капиллярная ячейка Рингбома представлена на рис. 1.2.8 и состоит из двух спаянных горизонтальных капилляров различных диаметров (0,726 10 –3 м и 0,343 10 –3 м), которые при помощи двух трехходовых кранов I и II соединялись с двумя колбами Е и F. Длина тонкого капилляра имела градуировку по периметру и равнялась 0,320 м , а длина большего капилляра – 0,13 м . Колба Е примерно наполовину заполнялась водой. Через патрубок G в колбу Е подавался СО₂ до полного насыщения воды. В колбу F подавали горячую воду и понижали давление с целью ее деаэрации. После этих операций в колбе F имели подготовленную к эксперименту деаэрированную воду, а в колбе Е – воду, насыщенную СО₂. Создав разрежение в капиллярах и используя трехходовые краны I и II, пространство соединительной трубки С заполняли насыщенной водой, а пространство трубки D – деаэрированной водой. После подготовки аппарата производили продувку и сушку капилляров путем пропускания сухого воздуха, а затем сухого исследуемого газа. По окончании продувки предварительно насыщенный парами воды газ подавался через кран I в капилляры, и создавалось давление меньше атмосферного на величину столба жидкости, достаточного для подачи жидкости из колбы Е к капилляру. Далее закрывали кран I и понижали давление на 130–170 мм рт. ст. (в СИ: 760 мм рт. ст. 0,1 МПа) ниже атмосферного и через кран II пускали в капилляр некоторое количество деаэрированной воды. Затем через кран I в капилляр впускали насыщенную воду таким образом, чтобы столбик жидкости оказался ближе к левой части градуированного тонкого капилляра [147].

Рис. 1.2.7. Принципиальная схема ячейки Стефана:
1 – капиллярная трубка; 2 – бачок с исследуемой жидкостью;
3 – перемещающийся столбик жидкости

Рис. 1.2.8. Схема капиллярной ячейки Рингбома

Во время диффузии столбик жидкости перемещается вправо, и, наблюдая за его перемещением, можно рассчитать D_АВ. Весь аппарат находился в термостате с прозрачными стенками для визуального наблюдения. Давление в колбе Е за время эксперимента практически не изменялось. Расчет велся по формуле (1.2.7).

Установка Рингбома имеет определенные недостатки, связанные с оценкой начального времени диффузии и начального объема газа. Чтобы исключить этот недостаток, Тамман и Джессен [147] предложили использовать следующую формулу для расчета:

, (1.2.8)

где DV – количество газа, поглощенного за время Dt.

Малик и Хайдук [193] применили вертикальный вариант ячейки с капилляром для диффузии ряда газообразных углеводородов в различные жидкости (рис. 1.2.9). Ячейка представляет собой вертикальный капилляр 1, внутренний диаметр которого был около 0,33 10 –3 м. Капилляр 1 спаян с другим капилляром 2, имеющим больший диаметр порядка 1 10 –3 м. Нижний конец этого капилляра вставлялся в ячейку 3. Ячейка 3 имеет два вакуумных крана 4 и 5, предназначенных для продувки и заполнения ячейки жидкостью. Диаметры капилляров тщательно измеряются. Конец капилляра 2, вставленный в ячейку, отшлифован на конус для того, чтобы обеспечить быстрый отвод продиффундировавшего газа и поддерживать около него практически нулевую концентрацию раствора.

Рис. 1.2.9. Капиллярная ячейка Малика и Хайдука:
1 – капиллярная трубка малого диаметра;
2 – капиллярная трубка бльшего диаметра;
3 – бачок с исследуемой жидкостью; 4, 5 – краны;
6 – капелька жидкости; 7 – насыщенная жидкость

Сама ячейка после тщательной продувки капилляра исследуемым газом заполняется деаэрированной исследуемой жидкостью 7. Предотвращение попадания жидкости в капилляр осуществляется закрытием крана 5. Для промывки и заполнения ячейки требуется не более 100 см 3 жидкости. По мнению авторов [193], это количество гарантирует наличие в ячейке жидкости без какой-либо примеси газа. После открывания крана 5, в капилляр поступает жидкость и образовывает столбик длиной l. Затем диффузионная ячейка помещается в термостатированную ванну и выдерживается определенное время, пока не устанавливается стационарный процесс диффузии через столбик жидкости в капилляре.

В процессе диффузии газа из объема, ограниченного этой каплей и столбиком жидкости в капилляре, капелька насыщенной жидкости перемещается вниз.

Перемещение положения капельки фиксируется катетометром 6 (рис. 1.2.10).

Рис. 1.2.10. Схема установки с капиллярной ячейкой
Малика и Хайдука:
1 – баллон с газом: 2 – сатураторы; 3 – диффузионная ячейка,
4 – шприц; 5 – краны; 6 – катетометр

Газ, перед подачей из баллона 1 в ячейку 3, насыщается парами исследуемой жидкости в сатураторах 2 путем барботажа его через данную жидкость.

Расчет ведется по формуле

, (1.2.9)

где п_А – массовый поток газа; l – длина столбика жидкости; c – общая массовая концентрация раствора;
– массовая концентрация газа на газожидкостной поверхности; С₀ – массовая концентрация газа в объеме жидкости.

Для определения времени начала стационарного процесса диффузии в капилляре авторы [193] применили уравнение

, (1.2.10)

при этом использовалось предполагаемое значение D_АВ для данной системы.

Результаты Малика и Хайдука для системы диоксид углерода(IV)–вода хорошо согласуются с результатами других исследователей, что говорит о надежной постановке эксперимента. Недостатками их установки является большая продолжительность эксперимента и необходимость создания равномерного спуска капли без залипаний.

Технические решения данного метода не ограничиваются конструкцией диффузионной ячейки с одним капилляром. Например, в [226] Росс и Гильдербранд применили набор таких капилляров для исследования диффузии газов в жидкостях. Их ячейка имела 254 отверстия диаметром 1 10 –3 м, которые были просверлены в стальной пластине диаметром 8 10 –2 м и толщиной 0,9131 10 –2 (рис. 1.2.11). Сверху в ячейку подается газ, снизу – деаэрированная жидкость, которая заполняет весь нижний объем ячейки и покрывает тонким слоем диафрагму с капиллярными отверстиями. Ошибка в точности полученных результатов составляет не более 5 %.

Рис. 1.2.11. Капиллярная диффузионная ячейка с большим количеством капилляров

Боэрбум и Клейн [60] применили горизонтальный вариант капиллярной ячейки, изучая диффузию инертных газов через столбик жидкости, окруженный с одной стороны диффундирующим газом, а с другой – газом-носителем. На рис. 1.2.12 представлена ячейка, примененная в [60], которая состоит из стеклянной колбы 1 объемом 2 см 3 и капилляра 2, площадь поперечного сечения которого составляет 1 мм 2 . Капилляр разделен двумя кранами 3 и 4 на части 5 и 6. Объем колбы 1 и диаметр капилляра тщательно промеряются. В начале эксперимента весь сосуд заполняется исследуемым газом. Затем краны 3 и 4 открываются, и тончайшим капилляром 8 вводится капелька исследуемой жидкости в положение 7 (как показано на рис. 1.2.12), которая образует столбик жидкости длиной около 3 10 –3 м. Авторы [60] считают, что если при заполнении ячейки жидкостью в колбу 1 и возможно попадание воздуха, то его количество крайне незначительно.

Рис. 1.2.12. Горизонтальная капиллярная ячейка:
1 – емкость с инертным газом; 2 – вход в капилляр;
3, 4 – краны; 5 – промежуточная емкость; 6 – газовая полость;
7 – капелька исследуемой жидкости; 8 – капилляр

После заполнения капилляра 8 жидкостью пространств 5 и 6 вводится несущий газ, и кран 4 закрывается. После определенного времени релаксации t_R, когда устанавливается стационарный процесс диффузии, приступают к измерению количества продиффундировавшего газа, анализируя отобранные из пространства 5 пробы с помощью масс-спектрометра. Длина столбика жидкости l определяется катетометром. Коэффициент молекулярной диффузии D_AB находят из уравнения

, (1.2.11)

где Q_A – количество продиффундировавшего газа, кмоль; F – площадь поперечного сечения капилляра, м 2 ; l – длина столбика жидкости в капилляре, м.

Время релаксации t_R авторы определяли приближенно по формуле, задаваясь возможным значением

. (1.2.12)

Стационарный процесс диффузии газа в жидкости, находящейся в капилляре, в техническом исполнении, как это видно из вышеизложенного, несложен и практически исключает конвекцию в жидкости. Однако искривленная межфазная поверхность, необходимость точных замеров диаметра капилляра по длине, допущение о неподвижности границ диффузионного потока и большая продолжительность эксперимента усложняют относительно простые расчеты и проведение эксперимента.

Метод насыщения из газовой фазы

Метод насыщения из газовой фазы предполагает диффузию газа через поверхность неподвижной жидкости. Данный метод применялся в [2, 3]. Для этого внутри термостатированного сосуда, соединенного с вакуумной установкой, располагают тонкостенные цилиндрические ампулы одинакового диаметра, но различной высоты, заполненные нелетучей жидкостью – в [2] октойлем, а также ампулу с летучей жидкостью – этанолом. При откачке воздуха из сосуда пары этанола приводятся в непосредственное соприкосновение с октойлем. После выдержки в течение определенного времени ампулы с раствором извлекаются из сосуда, закрываются крышками и взвешиваются. Было установлено [2], что график зависимости увеличения относительной массы раствора от обратной величины глубины слоя l раствора представляет собой: при малых – прямую, тангенс угла наклона которой определяется величиной , при больших – прямую, параллельную оси абсцисс, отсекающую на оси ординат величину , где m_B и m_A – соответственно массы растворителя и диффундирующего вещества. Отношение этих экспериментально определенных величин, равное , дает возможность вычисления коэффициента диффузии.

Метод насыщения жидкости из газовой фазы не требует сложных вычислений и сводится к задаче точного взвешивания.

Багров и др. [3] распространили метод насыщения из газовой фазы на системы с высокой растворимостью компонентов. При этом использовались два варианта определения коэффициента диффузии: по изменению давления газа и по изменению массы раствора при ограниченном количестве диффундирующего газа.

Схема установки для определения коэффициента диффузии по изменению давления диффундирующего газа представлена на рис. 1.2.13. Ампула с растворителем запаивается в отросток колбы 1, после чего воздух из колбы откачивается. Для того, чтобы точно фиксировать начало опыта, диффундирующее вещество испаряется в откачанный объем 2 из вспомогательной ампулы 3. Это позволяет за короткое время заполнить объем колбы 1 паром при помощи крана 4. Давление пара измеряется ртутным пьезометром с использованием катетометра. Начальное давление выбирается таким, чтобы изменение концентрации не превышало 2–4 %. Рабочий объем колбы ( 1 л ) и растворитель термостатируются при помощи теплообменника 5. Температура поддерживается с точностью 0,1 °С.

Рис. 1.2.13. Схема установки по методу насыщения из газовой фазы по изменению давления газа

С целью определения коэффициента диффузии снимаются кривые изменения давления пара от времени для различных начальных давлений диффундирующего пара и высот жидкости в ампуле.

Коэффициент диффузии рассчитывают из опытных данных с помощью формулы

, (1.2.13)

где – тангенс угла наклона к кривой зависимости изменения давления пара от корня квадратного от времени из точки при t = 0; Р₁ – начальное давление; l – глубина слоя жидкости в ампуле; А – параметр, определяемый из опыта.

Схема установки для определения коэффициента диффузии по изменению массы раствора показана на рис. 1.2.14.

Рис. 1.2.14. Схема установки по методу насыщения из газовой фазы по изменению массы:
1 – устройство для измерения перемещения чаши весов;
2 – ячейка с исследуемым раствором; 3 – герметичный теплоизоляционный корпус; 4 – ртутный дифманометр;
5 – колба с исследуемым газом; 6 – колба

Основной частью установки являются аналитические весы. На одном плече располагается ампула 2 с жидкостью. Изменение массы насыщаемой газом жидкости компенсируется при помощи соленоидов 1, через которые пропускается ток. Весы находятся под вакуумным колпаком. Давление диффундирующего пара, заполняющего колпак, определяется по ртутному дифманометру 4. Быстрое заполнение установки парами диффундирующего вещества достигается за счет того, что жидкость предварительно испаряется в баллон 5 большого объема. Установка термостатируется с точностью 0,05 °С. Изменение давления пара авторы связали с изменением массы раствора в процессе диффузии:

, (1.2.14)

где DQ – изменение массы в момент времени t; Р₁, Р₂ – начальное и конечное давление пара в течение эксперимента; V_п – объем пара при Р₁.

При проведении эксперимента при постоянном давлении пара используется та же установка, что и выше.

В результате была получена кривая прибавки массы жидкости от времени опыта. Начальный участок этой кривой описывается уравнением:

, (1.2.15)

где п_p – число частиц в единице объема раствора; S – площадь поверхности раствора; Не – константа Генри; DР = Р₁ – Р * ; Р₁ – начальное давление пара; Р * – равновесное давление пара.

Это уравнение в координатах – представляет прямую, наклон которой и конечное значение прибавки массы раствора позволяют определить D_АВ.

Методы определения коэффициентов
молекулярной диффузии из растворения
пузырька газа в жидкости

К настоящему времени разработано два метода, позволяющих определять коэффициент молекулярной диффузии при помощи растворяющихся пузырьков газа в жидкостях [58, 148, 279, 280]. Первый, так называемый DBS*-метод [58], заключается в измерении уменьшения диаметра пузырька в течение времени. Второй – СBS**-метод, согласно которому измеряется количество добавленного к пузырьку газа, чтобы поддерживать его размер постоянным [58].

Метод уменьшающегося пузырька

Впервые изучение скорости массопереноса при растворении маленьких (до 0,4 мм ) неподвижных пузырей газа в жидкости с целью определения коэффициентов диффузии было выполнено Мэйчем [148]. В работе были получены коэффициенты диффузии воздуха в воде, однако, согласно [148], значения D_AB оказались значительно заниженными. Брандштейер [148] повторил работу Мэйча и объяснил занижение результатов наличием на поверхности пузырька загрязнений. Либерман [176] и Мэнли [194], изучая скорость растворения неподвижных пузырей в частично насыщенной воде, обнаружили, что скорость диффузии у пузырьков малого диаметра ниже, чем предполагает теория. Это различие между теорией и экспериментом они также объяснили наличием мельчайших примесей, которые образуют пленку вокруг маленьких пузырей. Наиболее полное развитие DBS-метод получил в работах Хоугтона и др. [148], а также Вайса и Хоугтона [279, 280], которые определили коэффициенты диффузии более 15 различных газов в воде в широком ряде температур. Схема установки для определения D_AB, которая использовалась в [148], показана на рис. 1.2.15, а. Ячейка представляет собой вертикальный прямоугольный сосуд (длина – примерно 0,076 м , ширина – 0,045 м , толщина – 6 10 –3 м) и была выполнена из U-образной узкой стеклянной полосы 1 толщиной 3 10 –3 м, на которую наклеивались две 1,5 миллиметровые пластины 2. В верхней части имелась стеклянная пробка 3, которая закрывала доступ воздуха в ячейку при работе.

Воду специально подготавливают, удаляя растворенный в ней воздух путем кипячения в круглодонной колбе в течение 45 мин. Перед экспериментом диффузионную ячейку промывают этой водой и только потом окончательно заполняют до самого верха. Для получения мелких пузырей применяют следующая процедура. Микрометрический шприц частично заполняют из специальной системы исследуемым газом и затем вводят в ячейку с целью получения пузырька диаметром 1–2 мм, который закрепляется на стенке, заполненной водой ячейки около вершины. Затем этот пузырек засасывается обратно в шприц вместе с некоторым количеством воды, а потом содержимое быстро впрыскивается обратно в ячейку, наклоненную под углом 30° к горизонтали. При этом образуется несколько очень маленьких пузырьков, закрепленных на стенке ячейки и удерживающихся на ней за счет сил поверхностного натяжения. Ячейка быстро ориентируется относительно объектива микроскопа так, чтобы пузырек, оказавшийся посреди ячейки, был в фокусе объектива. Секундомер включают сразу же после образования пузырька, а его диаметр измеряется в зависимости от времени. Шкала объектива микроскопа калибруется на стандартной ( 0,1 мм ) шкале так, чтобы изменение диаметра пузырька до 0,003 мм можно было легко заметить. Увеличенная часть ячейки с объективом, ориентированным на пузырек, показана на рис. 1.2.15, б. Для получения коэффициента диффузии измеряются около 10 пузырьков данного газа, причем каждый раз используются свежие пробы воды и газа. Затем экспериментальные данные осредняются.

Для определения коэффициента диффузии строится зависимость изменения d 2 _П от t, где d_П – мгновенное значение диаметра пузыря, измеренного под микроскопом. Было установлено [148], что полученные данные нельзя описать одной прямой линией, однако они хорошо аппроксимируются двумя прямыми, имеющими различный наклон [148]. Эти две прямые линии определяют скорость абсорбции в начале и конце эксперимента. Мэйч, который впервые получил эти данные, принял средний наклон графика, однако, как указывалось выше, получил низкие значения D_AB. На основании работ Либермана [176] и Мэнли [194], которые высказали мнение, что изменение наклона вызвано накоплением поверхностно-активных веществ на поверхности пузырька, Хоугтон заключил, что именно первоначальный наклон должен использоваться в расчете коэффициентов диффузии. В [148] применялся именно первоначальный наклон графика, и коэффициент диффузии определяется по формуле

(1.2.16)

где т – первоначальный наклон графика зависимости от ; Т – температура; a – коэффициент абсорбции Бунзена.

Рис. 1.2.15. Вертикальная диффузионная ячейка
для определения D_AB пo DBS-методу [148]:
а) схема ячейки;
б) увеличенная часть ячейки с объективом

Другой вариант установки (рис. 1.2.16) для определения коэффициента диффузии по DBS-методу использовался в [279, 280]. Здесь ячейка, в которую вводился пузырек, располагается горизонтально и пузырек закрепляется также с помощью сил поверхностного натяжения на верхней поверхности. Прозрачная ячейка 1 изготовляется из прозрачного специального материала толщиной 1,5 10 –3 м и размерами 55 6 5 мм. Эта ячейка заключена в водяную рубашку 2 размерами 70 20 11 мм и имеет прозрачные стенки. Вода протекает по щелевому пространству со скоростью порядка 1 л/мин, осуществляя термостатирование ячейки 1. Температура жидкости в ячейке измеряется термопарой 3. Единственное отверстие, ведущее к ячейке 1, позволяет вводить с помощью шприца исследуемые жидкости и газ. Образование пузырьков аналогично предыдущей работе. Ввиду того, что проводимые исследования в [279, 280] были при повышенных температурах (до 60 °С), это привело к тому, что использование вертикального варианта оказалось сложным с точки зрения закрепления пузырька в середине ячейки с помощью сил поверхностного натяжения. Техника образования большого пузыря, а затем маленьких из газожидкостной смеси обеспечивала то, что внешнее давление водяного пара находилось первоначально в равновесии с жидкостью. Коэффициент диффузии определяется по формуле

, (1.2.17)

где Р_d – барометрическое давление (обычно около 750 мм . рт. ст.); Р – давление водяного пара, мм. рт. ст.

Рис. 1.2.16. Горизонтальная диффузионная ячейка
для определения D_АВ пo DBS-методу [280]:
а) схема ячейки; б) увеличение пузырька;
1 – кювета с исследуемой жидкостью и пузырьком газа;
2 – тепловая жидкостная рубашка; 3 – термопара;
4 – окуляр микроскопа

Числовой коэффициент 3,00 в формуле (1.2.17) был определен при калибровке ячейки на системе кислород–вода. Коэффициент диффузии кислорода был определен с точностью до 1 % методом полярографии и равен 2,6 10 –5 см 2 /с при 20 °С. Погрешность экспериментального метода, согласно [148, 280], составляла ± 10 %.

Метод постоянного диаметра пузырька

Допущение наличия массопереноса от сферы в жидкое безграничное пространство при экспериментальном исследовании по DBS-методу не выполняется, т. к. пузырек закрепляется на непроницаемой стенке и, следовательно, часть поверхности пузырька в процессе массопереноса не участвует. С другой стороны, при диффузии происходит уменьшение пузырька и его центр движется радиально по направлению к стенке, следовательно, массоперенос частично будет конвективным [58]. Чтобы избежать этих двух основных недостатков DBS-метода, был разработан CBS-метод [58, 59], согласно которому коэффициент молекулярной диффузии определяется из объема газа, который добавляется за единицу времени к газовому пузырьку для поддержания его диаметра постоянного размера. На рис. 1.2.17 показан газовый пузырек, закрепленный на конце иглы шприца 2, имеющей форму усеченного конуса. Центр газового пузырька совпадает с гипотетическим основанием этого конуса. Для нестационарной диффузии газа А через межфазную поверхность в неподвижный растворитель В уравнение непрерывности для сферических координат [58]:

; (1.2.18)

граничные и начальные условия:

(1.2.19)

где r – полярная координата; R – радиус пузырька; t – время; С_A – концентрация газа в растворе.

Рис. 1.2.17. Расчетная схема определения D_АВ
пo CBS-методу [58]:
1 – плунжер; 2 – игла

Для этих условий найдено следующее решение

, (1.2.20)

; (1.2.21)

С_R – концентрация газа у поверхности контакта фаз при r = R; С – концентрация газа в растворе при r = 0 и r = для t > 0.

Мольный поток газа на поверхности контакта фаз может быть записан [58] как

. (1.2.22)

, (1.2.23)

где Q – полярная координата, радиан.

Тогда часть поверхности пузырька, доступная массопереносу:

, (1.2.24)

и скорость абсорбции через поверхность пузырька, закрепленного на игле, будет

(1.2.25)

Общее число молей А, диффундировавших в жидкость за время t = t‘, находится интегрированием уравнения (1.2.25):

(1.2.26)

Концентрация газа в жидкости у поверхности контакта фаз определяется законом Генри:

, (1.2.27)

где Не – константа Генри; Р_R – парциальное давление газа при Т, Па.

Допуская, что газ идеальный, объем поглощенного газа A равен:

. (1.2.28)

Из уравнений (1.2.26) и (1.2.27) можно записать:

(1.2.29)

Уравнение (1.2.29) может быть представлено в виде уравнения прямой линии, проходящей через начало координат:

(1.2.30)

Коэффициент диффузии определяется по наклону т прямой линии:

. (1.2.31)

Данный метод расчета рассматривает только пузырьки определенного диаметра, т. е. те, у которых центр совпадает с гипотетической вершиной усеченного конуса (рис. 1.2.17). Экспериментальная установка по CBS-методу представлена на рис. 1.2.18.

Диффузионная ячейка состоит из двух маленьких стальных цилиндрических трубок остановленных концентрично одна в другой. Малый цилиндр 1 имеет внутренний диаметр 15 10 –3 м, а внешний – 20 10 –3 м. Его длина – 20 10 –3 м. Оба конца внутренней ячейки закрыты пограничными пластинами, которые запрессованы в О-образные фланцы для предотвращения утечки. Цилиндр 2 имеет внутренний диаметр 50 10 –3 м, а наружный – 70 10 –3 м. Его длина 47 10 –3 м, а оба конца закрываются круглыми прозрачными пластинами из стекла того же диаметра. В пространство между цилиндрами подается вода из термостата, и ее температура поддерживается с точностью до ± 0,5° С. Температура определяется термометром сопротивления, введенным внутрь цилиндра. Дегазированная жидкость подается и отводится через капилляры диаметром 1 10 –3 мм и 1,5 10 –3 мм соответственно. Вход ячейки соединяется с маленькой воронкой 4 для поддержания более высокого уровня. Вход соединяется с открытым манометром 5, чтобы выравнить давление газа в пузырьке с барометрическим и предотвратить утечку через плунжер шприца 7. Сосуд 8 перемещается в вертикальном направлении так, чтобы уровень жидкости в нем совпадал с высотой положения газового пузырька на игле шприца. На дне ячейки располагается небольшой цилиндр 9 с внутренним диаметром 3 10 –3 м и наружным 5 10 –3 м, закрытый с обеих сторон перегородками. Этот цилиндр большей частью окружен водой из термостата. Для измерения диаметра пузырька используется оптическая система (рис. 1.2.19). Пузырек газа и конец иглы проектировались со стократным увеличением на экран.

Рис. 1.2.18. Схема экспериментальной установки по CBS-методу [58]:
1 – диффузионная ячейка; 2 – наружный цилиндр;
3 – термопара; 4 – воронка; 5, 8 – устройство для подачи
и поддержания постоянного давления жидкости;
6 – пузырек; 7, 9 – термостатируемое устройство
для создания пузырька газа в ячейке; 10 – микрометр

Рис. 1.2.19. Схема оптической системы для CBS-метода [74]

В оптической системе (рис. 1.2.19) ячейка располагается между источником света 2 с диафрагмой 3 и несколькими линзами 4–6. С помощью диафрагмы 3 уменьшается интенсивность освещения, чтобы устранить местное нагревание жидкости во внутреннем сосуде и, как следствие, избежать свободной конвекции жидкости около пузырька. Изображение иглы с пузырьком отражается в зеркале 7, чтобы получить уже увеличенное изображение на экране 8, помещенном в стороне от ячейки.

Перед началом эксперимента внутренняя ячейка 1 промывается и заполняется дегазированной жидкостью примерно на 1/3 своего объема. Затем конец иглы проходил через нижнюю перегородку цилиндра 9 (рис 1.2.18) и цилиндр 9 опорожняется. После достижения вакуума цилиндр 9 заполняется газом, коэффициент диффузии которого должен быть определен.

Эта процедура повторяется 5 раз. При помощи втягивания плунжера в шприц 7 газ заполняет иглу. После того, как игла проходит через верхнюю перегородку цилиндра 9 в дегазированную жидкость, шприц фиксируется, а микрометр 10 завинчивается, чтобы передвинуть плунжер наверх и образовать пузырек требуемого диаметра. Размер пузыря проверяется на экране. Требуемый диаметр пузырька определяют из величины угла и диаметра усеченного конуса, измеряемых на экране:

. (1.2.32)

Истинный диаметр пузырька определяют из

, (1.2.33)

где – отношение между истинным диаметром конца иглы и ее увеличенным изображением на экране. Микрометр подкручивается вручную так, чтобы на экране получался пузырек требуемого диаметра. Показание микрометра записывается. В течение следующих 11 мин газ постоянно подается так, чтобы, несмотря на диффузию, диаметр пузырька оставался постоянным, а показания микрометра записывались каждые 60 с. Общий объем диффундировавшего газа V_A(t) за время t = t измеряют умножением перемещения микрометра за время t = t₀ на площадь поперечного сечения плунжера. Ошибка в расчете коэффициента диффузии, по мнению авторов [58], по данному методу составляет ± 2 %, и измерение величины D_AB не требует дальнейшей корреляции.

Полярографический метод определения коэффициентов молекулярной диффузии газов
в жидкости

Полярографический метод является одним из основных методов физико-химического анализа и был успешно применен в [156, 165] для определения D_AB газов в жидкостях.

Процесс поляризации на ртутно-капельном электроде был исследован Ильковичем и достаточно подробно описан в [21, 164]. При снятии вольт-амперных характеристик ртутно-капельного электрода было установлено, что существует зона, где величина тока зависит только от диффузии молекул газа. Эта величина тока i_D была названа предельным диффузионным током и определяется как горизонтальная область на вольт-амперной характеристике (рис. 1.2.20). В этой области i_D не зависит от прилагаемого потенциала, a D_АВ описывается следующее зависимостью:

(1.2.34)

где i_D – сила диффузионного тока; Z – валентность восстанавливаемого иона; C – концентрация растворенного газа; m – масса ртути, вытекающей из капилляра за 1 с; t – время образования капли.

Из величин, входящих в уравнение Ильковича, влиянию температуры подвержены m и t, которые в свою очередь влияют на i_D и, соответственно, на D_AB. Кроме того, температура оказывает и непосредственное влияние на величину коэффициента диффузии, и поэтому ее необходимо поддерживать как можно с большей точностью.

Рис. 1.2.20. Вольт-амперная характеристика
ртутно-капельного электрода

Конструкция ртутно-капельного электрода подробно описана в [21, 164, 165]. Для определения характеристик капилляра 50100 капель ртути отбирают при определенном потенциале (чаще 0,6 В, а иногда и без наложения потенциала), и определяют их массу взвешиванием. Время образования капель определяют по секундомеру. По этим данным находят константу капилляра m 2/3 t l/6 . Значение константы капилляра зависит не только от его свойств, но и от высоты столба ртути, поэтому она должна быть постоянной в эксперименте. Схема ячейки с ртутно-капельным электродом, согласно работе Кольтгоффа и Миллера [165], дана на рис. 1.2.21. Насыщенный каломельный электрод 6, 7, 8, 9 помещается во внутрь солевого раствора до начала эксперимента. Широкая трубка 6 запаивается внутри каломельной части ячейки и заполняется 3% гелем агара 4, насыщенным KCl (5). Величина поверхности ртути в насыщенной части ячейки около 8 см 2 . Время образования капли – 4 с.

Рис. 1.2.21. Ртутно-капельный электрод

Позднее Джордан, Аккерман и Бергер [156] использовали полярографический метод для определения D_AB кислорода в водные растворы сахарозы и глицерина. При этом для расчета D_AB они использовали модифицированное уравнение Ильковича

, (1.2.35)

Значение растворимости С определяется экспериментально по методу Винклера с точностью до ± 1 %. Авторы [156] показали, что значения D_AB, рассчитанные по уравнению (1.2.34), дают значения, заниженные на 10 % по сравнению с уравнением (1.2.35). Полярографический метод определения D_AB достаточно точен, однако сложен и требует дальнейшего экспериментального сравнения с другими методами.

Метод Тэйлоровской диффузии
в ламинарном потоке

Поиск новых методов экспериментального определения коэффициентов молекулярной диффузии растворенных газов в жидкости привел ряд исследователей [54, 70, 71, 76, 214, 243] к разработке нового метода – метода Тейлоровской диффузии растворенного газа в ламинарном потоке растворителя.

Принцип реализации этого метода заключается в следующем. Растворитель движется стационарным потоком по длинной трубке (L 2R) в ламинарном режиме. На входе в эту трубку производится внезапный (импульсный) ввод диффундирующего вещества, а на другом конце трубки фиксируется его дисперсия в осевом направлении. На рис. 1.2.22 представлена схема Тэйлоровской диффузии в ламинарном потоке растворителя. На начальном участке трубки при импульсном вводе диффундирующего вещества А по всему сечению образуется область шириной DХ с концентрацией С₀. В дальнейшем, ввиду параболического профиля скоростей, характерного для ламинарного режима движения потока, эта область стремится перейти от прямоугольного распределения концентрации также к параболическому. Если бы молекулярная диффузия не происходила, то такой характер распределения концентрации диспергированного вещества сохранялся бы до выхода потока из трубки. Однако в результате существования молекулярной диффузии происходит быстрое выравнивание концентрации диффундирующего вещества по сечению трубки. Далее, если диаметр трубки намного меньше ее длины (2R L), то молекулярной диффузией вдоль оси пренебрегают по сравнению с диффузией в радиальном направлении. В результате наличия радиальной диффузии (рис. 1.2.22) происходит осевое перераспределение концентрации диффундирующего вещества с образованием области шириной DХ₁. Было установлено [76, 214, 243], что осевое распределение средней (по сечению) концентрации является Гауссовым относительно плоскости, движущейся со скоростью U_cp, причем максимальная концентрация в любой точке сечения выражена довольно резко (т. е. имеется пик концентрации). Изменение концентрации в конце трубки фиксируется любым из применяемых к данной системе газ–жидкость чувствительных датчиков, рассмотренных ниже.

На основании Гауссова распределения концентрации средняя концентрация на расстоянии X₁ от точки ввода вещества может быть рассчитана как [54]

Рис. 1.2.22. Диффузия по Тейлору в ламинарном потоке растворителя

, (1.2.36)

где K – «виртуальный» или эффективный коэффициент переноса в направлении движения.

. (1.2.37)

В случае Тэйлоровской диффузии влиянием осевой диффузии на K можно пренебречь, тогда уравнение (1.2.37) сводится к виду

, (1.2.38)

. (1.2.39)

Использование уравнения (1.2.39) возможно, если определить значение K, которое, в свою очередь, связано с величиной дисперсии s 2 следующей зависимостью

, (1.2.40)

где – время, которое проходит между моментом ввода растворенного вещества в поток и моментом прохождения максимума пика концентрации.

Болдауф и Кнапп [54] показали, что величины s_t и t_l могут быть определены из следующих выражений:

(1.2.41)

. (1.2.42)

Оценка экспериментальных данных, связанных с нахождением s_t и , может вестись различными методами, наиболее простым из которых является графический [54]. Этот метод основан на измерении величины по графику изменения сигнала от чувствительного элемента, фиксирующего изменение концентрации диффундирующего вещества во времени. Пример такого графика представлен на рис. 1.2.23. Из графика могут быть определены: t_W – интервал времени между точками перегиба, или t₁₂ – интервал времени между точками 2 и 1, или t_В – интервал времени между пересечениями касательных в точках перегиба.

, (1.2.43)

то для нормального Гауссова распределения

. (1.2.44)

Другие численные методы оценки D_АВ обсуждаются в [54], однако они являются более сложными и требуют использования вычислительной техники.

Рис. 1.2.23. Графический метод оценки распределения концентраций по оси потока

Экспериментальная установка, реализующая метод Тэйлоровской диффузии в ламинарном потоке растворителя, достаточно проста и схематично представлена на рис. 1.2.24.

Рис. 1.2.24. Схема установки для определения D_AB по методу Тейлоровской диффузии в ламинарном потоке растворителя

Установка состоит из напорного бака 1 с растворителем, капиллярной трубки 2, в которой осуществляется процесс диффузии, шприца 3 для ввода диффундирующего вещества в трубку, анализатора распределения концентрации растворяемого вещества 4, термостатированного бака 5, в котором располагается капиллярная трубка 2, свернутая для удобства в змеевик, а также сатураторы для приготовления проб диффундирующего газа.

Измерение коэффициентов молекулярной диффузии растворенных газов в жидкости производится следующим образом. После термостатирования всей установки до температуры эксперимента растворитель из напорного бака 1 подается в капиллярную трубку 2 длиной 710 м, затем на входе в трубку вводится специально подготовленная проба диффундирующего газа. Для этого часть растворителя отдельно насыщается исследуемым газом и отбирается в шприц 3. После этого пробу импульсно вводят через резиновую перегородку в трубку 2. Далее проба диффундирует в ламинарном потоке, и в результате Тэйлоровской диффузии наблюдается дисперсия вещества в направлении движения. Распределение концентрации диффундирующего газа на выходе фиксируется одним из известных способов, позволяющих оценивать количество растворенного газа в жидкости. Следует отметить, что абсолютное значение концентрации растворенного газа может и не определяться, т. к. эта величина не требуется для расчета D_АВ, особенно в тех случаях, когда D_АВ не зависит от концентрации. В качестве датчика для определения концентрации растворимого газа на выходе из трубки 2 могут использоваться рефрактометр [214] или полярографический микроэлектрод [243]. Может использоваться и стандартное Лабораторное оборудование, применяемое для жидкостной хроматографии [54].

Для того, чтобы гарантировать ламинарный режим потока растворителя в трубке, рекомендуется [214] проводить исследования при числах Рейнольдса Re 40. Важным является правильный выбор длины трубки, что позволяет создать необходимые условия для развития осевой дисперсии. Пратт и Уэйкхэм [214] показали и экспериментально подтвердили, что время, необходимое для реализации Тэйлоровской диффузии в ламинарном потоке, можно оценить из зависимости

. (1.2.45)

Другим не менее важным условием является то, чтобы ввод инжектируемой пробы был импульсным. Это условие будет сохраняться, если объем пробы V_П будет намного меньше объема V_T трубки 2.

Пратт и Уэйкхэм [214] рекомендуют V_П

* DBS (decrease bubble size) – метод уменьшающегося размера пузырька.

** СBS (constant bubble size) – метод постоянного размера пузырька.

Источник