Способы определения формы связей между показателями.
Предмет эконометрики, её связь с другими науками
Термин «эконометрика» возник в 20 веке и изучает количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей.
Эконометрика- это наука, изучающая количественные закономерности экономических явлений и процессов, с помощью статистических методов и моделей.
Эконометрика дает инструментарий для экономических измерений, а также методологию оценки параметров моделей микро и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий.
Эконометрика входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрия, наукометрия, психометрия, хемометрия, квалиметрия. Особняком стоит социометрия — этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, то есть за небольшой частью такой дисциплины, как статистический анализ в социологии
Этапы эконометрического исследования.
1. Постановка проблемы.
2. Получение данных и анализ их качества.
Данные должны быть получены по однородной совокупности и не смешивать явления.
3. Спецификация модели. Спецификация – выбор показателей и конкретной модели (конкретных показателей которые будут исследованы, выбор определенной модели решения.) Она тесно связана с постановкой проблемы.
4. Оценка параметров модели. Некоторые параметры являются константами.
y = a+bx ; a и b — параметры, y и x –переменные.
Данные обладают свойствами как, ошибки наблюдения и ошибки выборочного наблюдения.
Все данные являются выборочными полученные на 2-ом этапе, поэтому параметры модели рассчитанные по этим данным являются не точными значениями этих (истинных) параметров, а их оценкой. Кроме самих параметров на этом этапе оцениваются их качество.
5. Интерпретация и использование результатов исследования (прогнозирование)
Виды эконометрических моделей.
Эконометрические модели можно классифицировать по:
Видам связей между показателями.
А)Стахастические – эти связи имеют элемент случайности. Частный случай стахастических связей — это корреляционные связи.
Корреляционная связь – это связь при котором конкретным значением фактора соответствует определенные средние значения результата, т.е. функциональные зависимости. Например: средняя стоимость проезда зависит от расстояния, значение результата , которое было рассчитано по модели отражающую корреляционную связь, путем подстановки в нее значения факторов, называется выровненным или теоретическим значением результата и обозначается ŷ
Отклонение фактического значения результата от выравненного, определяется случайными факторами. Не может быть точно рассчитано заранее до проведения наблюдения, называемое отклонение – есть случайный остаток или случайное отклонение (ошибка) и обозначается ε
Функция которая отражает зависимость выравненных значений результатов от значений фактора называется функцией регрессии, или эта функция отражает корреляционную связь между показателями.
Модель включает в себя регрессию и может включать тождество
Б) Функциональные – это связи где значение одних показателей однозначно определяет значение других показателей. Те показатели которые оказывают влияние называются независимыми переменными – факторы(х)
Показатели на которые оказывается влияние называются зависимые переменные – результатами(у)
Частный случай функции связи:
y = x + z , z – тоже фактор. y-доход, x- расход, z- накопление.
Такое выражение называется тождеством, в нем все параметры известны.
2. По количеству уравнений входящих в эконометрическую модель. Модель может состоять из одного уравнения – регрессии, или нескольких уравнений – система эконометрических уравнений.
3.По форме функции использованной в регрессии. Соответственно различают линейные и нелинейные регрессии.
4.По количеству факторов входящих в уравнение регрессии. С одним фактором – парная регрессия ( результат и фактор), если 2 и более – множественная.
По типу данных.
А) простейшая модель(классическая нормальная линейная модель)
Б) более сложная – модель с фиктивными переменными (хотя бы один из факторов является неколичественной переменной)
В) Логит и пробит модели – это модели в которых результат является неколичественной переменной и может принимать два значения либо количественное с переменной значением 0;1,
Г) Модели с цензурированными данными и тобит модели – это модели у которых на значение результата наложены ограничения не ниже, не выше.
Д) модели временного ряда
yt =a + bt + ε — модель Тренда
t- номер момента времени
y- показатель который меняется во времени, итд
По временной принадлежности данных.
А) пространственные данные – это данные взятые для разных единиц совокупности, в один и тот же момент времени.
Б) модели с временными данными. Это данные взятые для одной совокупности в разные моменты времени.
В) Модели с панельными данными. Модель для данных объединяющая предыдущие 2 типа.
Способы определения формы связей между показателями.
Определение формы — это выбор конкретной математической функции которая описывает определенную связь.
1-й способ Графический
Достоинство этого метода наглядность
Недостаток – неточность. Можно найти конкретный результат(частный график), но невозможно построить общий график
2-й способ Теоретический (аналитический).
Из предыдущих исследований известны сведения о форме функции.
3-й Экспериментальный.
Основной метод который предполагает расчет параметров разных функций(на основе наших исходных данных) и выборе из этих функций наилучшей по определенным критериям. Основной задачей экспериментального способа – это анаиз зависимости между переменными показателями. Значимость может быть функциональной или статистической.
Функциональная (детерминированная) зависимость – задается в виде формулы, которая каждому значению одной переменной ставит в соответствие строго определенное значение другой переменной(воздействием случайных факторов при этом принебрегают).
Статистическая зависимость – это связь переменных на которую накладывается воздействие случайных факторов. При этом изменение одной переменной приводит к изменению математического ожидания – наиболее вероятного ожидаемого значения другой переменной. Уравнение регрессии – это формула статистической связи между переменными. Если эта формула линейна, она представляет собой линейную регрессию, а если нелинейная, то представляет собой нелинейную регрессию.
Источник
Способы определения формы связи между показателями
Один из этапов эконометрического исследования — это спецификация моде- ли, в которую входит отбор фактора и выбор формы функции, о выборе формы функции и пойдет речь.
В эконометрике всегда отдается предпочтение простым функциям пе- ред сложными. Поэтому самая популярная – самая простая – это линейная функция.
Способы выявления формы функции:
1. Графический способ. Это поле корреляции (см. рис. 1, стр. 7).
Достоинство графического метода, во-первых, в его наглядности. Но этот метод подходит с трудом, если у нас много факторов, трехмерное пространство еще как-то можно изобразить, а четырехмерные модели не изобразить.
2. Теоретический (аналитический метод). Для исследователя это самый простой метод, потому что исследовать ничего не надо, а надо просто опереться на предыдущие знания, исследования, опыты, из них можно выявить форму функции.
3. Экспериментальный метод, который заключается в том, что находят параметры разных функций (линейной, нелинейной и проч.) и по опре- деленным критериям выбирают наилучшую функцию, функцию кото- рая наилучшим образом отражает закономерность. Чем ближе функ- ция подходит к нашим точкам, тем лучше.
Источник
Основные формы корреляционной связи между признаками
Выявлению формы связи между признаками предшествует определение причинной зависимости между ними. Это наиболее важный и ответственный момент для правильного использования корреляционного метода. По каждому изучаемому явлению предварительно необходимо установить, какие логические причины лежат в основе связи между признаками-факторами и признаками-результатами.
Выявление формы связи между признаками сводится к выбору математического уравнения, которое могло бы наиболее полно и точно отразить характер взаимосвязи между изучаемыми признаками. Любая форма корреляционной связи между признаками, выступая как внешнее проявление причинно-следственной зависимости в экономических явлениях, естественно, отражает и общий характер внутреннего содержания этой взаимосвязи. Поэтому установление формы связи между признаками –– важный этап изучения корреляционной зависимости.
Влияние одного или нескольких факторов на результативный признак приводит к формированию различных по содержанию и форме корреляционных зависимостей. В экономических явлениях могут иметь место самые разнообразные формы корреляционной связи, так как с возрастанием факторного признака возможно не только более-менее равномерное увеличение или убывание признака-результата, но и неравномерное, непропорциональное его изменение. В связи с этим различают близкую к прямолинейной и криволинейную формы простой (парной) корреляционной связи.
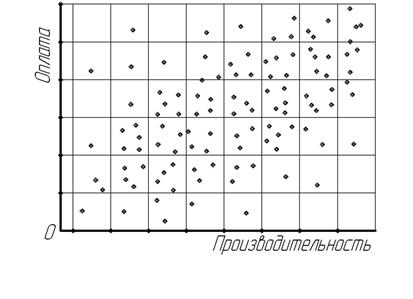
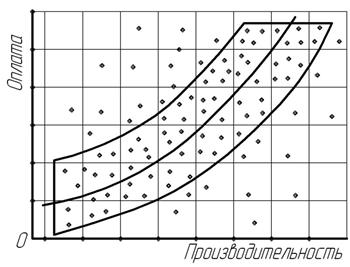
Для ориентировочного выявления эмпирической формы корреляционной зависимости могут применяться различные статистические приемы, среди которых наиболее распространенный, наглядный и доступный – графический способ. На координатной диаграмме, где по оси абсцисс откладывают значения признака-фактора, а по оси ординат – значения признака-результата, изображают поле корреляции (рис.11.1), которое представляет собой совокупность точек, размещенных на плоскости в системе координат.
Рис. 11.1. Поле корреляции, характеризующее взаимосвязь годовой производительности и оплаты труда в организациях АПК
Эмпирическую форму корреляционной связи обычно выявляют по направленности основной массы точек, сосредоточенных в поле корреляции. Наглядным естественным примером корреляционного поля может служить Млечный путь, где наблюдается повышенная концентрация звезд. Вытянутость этого пути с востока на запад указывает на форму, близкую к прямолинейной.
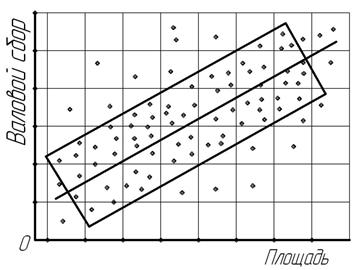
Прямолинейная простая (парная) корреляционная зависимость характеризуется возрастанием или убыванием на более-менее определенную величину результативных признаков при непрерывном возрастании факторных признаков. При прямой, близкой к прямолинейной, корреляционной связи увеличение фактора сопровождается повышением результата, при обратной – рост факторного признака вызывает снижение результативного. Графическое изображение прямой и обратной корреляционной связи показано на рис.11.2 и 11.3.
Рис. 11.2. Взаимосвязь валового сбора и посевной площади картофеля в крестьянских (фермерских) хозяйствах (корреляционная прямая зависимость)
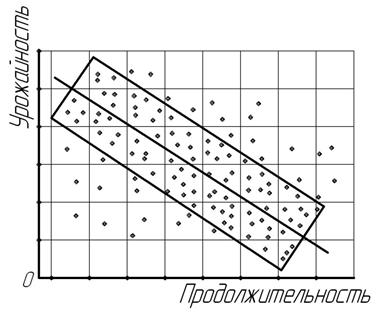
Рис. 11.3. Взаимосвязь урожайности и продолжительности уборки зерновых культур в сельскохозяйственных организациях (корреляционная обратная зависимость)
Основная масса точек на этих рисунках ограничена прямоугольниками и проведены эмпирические прямые линии регрессии, предназначенные для лучшего понимания не только формы, но и содержания прямолинейной (прямой и обратной) корреляционной зависимости. На рис.11.2 наглядно видно, что рост фактора вызывает почти прямолинейное повышение результата, а на рис.11.3 –– увеличение факторного признака сопровождается близким к прямолинейному снижением результативного признака.
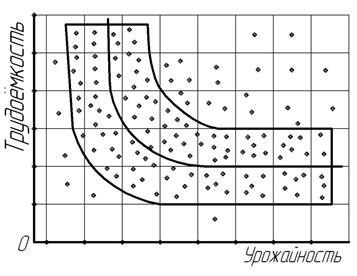
Криволинейные парные корреляционные связи в экономических явлениях могут выражаться в разнообразные формах: гиперболической, параболической, экспоненциальной, синусоидальной и т.д. Для наглядного представления о некоторых формах корреляционной зависимости приведено их графическое изображение (рис. 11.4 – 11.6).
Рис. 11.4. Взаимосвязь трудоёмкости и урожайности сахарной свеклы в сельскохозяйственных организациях (корреляционная гиперболическая зависимость)
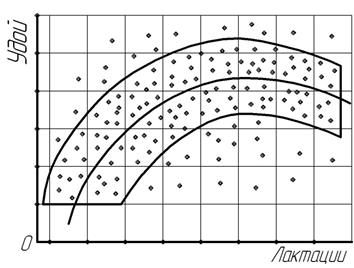
Рис. 11.5. Взаимосвязь годового удоя и числа лактаций коров в сельскохозяйственных организациях (корреляционная параболическая зависимость)
Рис. 11.6. Взаимосвязь коммерческих цен и темпов роста инфляции
(корреляционная экспоненциальная зависимость)
На рис. 11.4 видно, это рост признака-фактора на начальной стадии приводит к резкому падению, а в дальнейшем – замедленному снижению признака-результата. Это характерная особенность гиперболической формы корреляционной связи. В отличие от предыдущей формы зависимости, на рис. 11.5 показана более сложная, параболическая корреляционная связь, где изменение результативного признака можно условно разделить на три стадии: на начальной наблюдается довольно быстрое повышение, далее признак-результат достигает апогея и, наконец, этот же признак претерпевает существенный спад.
Выявление и установление формы корреляционной зависимости –– одна из важнейших задач корреляционно-регрессионного метода. Во-первых, значение конкретной формы связи способствует поиску наиболее точного способа измерения тесноты связи между факторным и результативным признаками; во-вторых, это облегчает выбор корреляционного уравнения регрессии, которое в наибольшей мере соответствует содержанию и характеру корреляционной зависимости.
Множественная корреляция, т.е. статистическая зависимость результативного признака от нескольких признаков-факторов, по форме не отличается от парной корреляционной связи. Вместе с тем выявление формы множественной связи в значительной мере затруднено. Поэтому решению множественного корреляционного комплекса обычно предшествует разработка соответствующих вопросов по однофакторным корреляционным моделям.
Источник
