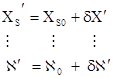Способы определения элементов внешнего ориентирования снимка

Определение элементов внешнего ориентирования снимка по опорным точкам (обратная фотограмметрическая засечка)

Опорной точкой будем называть точку, опознанную на местности и на снимке, геодезические координаты которой на местности известны.

Для определения элементов внешнего ориентирования снимка воспользуемся уравнениями коллинеарности (1.3.12), которые представим в виде

; (1.5.1)

;

. (1.5.2)

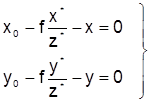
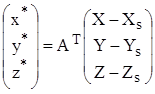
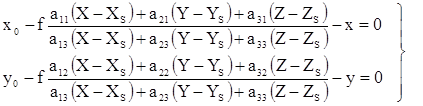
Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.5.2), в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, геодезические координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования снимка f,x₀,y₀.

Неизвестными величинами в уравнениях (1.5.2) являются 6 элементов внешнего ориентирования снимка Xs, Ys, Zs, w, a, À.

Следовательно, для определения 6 неизвестных элементов внешнего ориентирования снимка достаточно иметь не менее 3 опорных точек. При этом опорные точки на местности не должны располагаться на одной прямой. Если имеются 3 опорные точки, координаты изображений которых на снимке измерены, можно составить систему из 6 уравнений (1.5.2) с 6 неизвестными. В результате решения этой системы уравнений можно найти значения элементов внешнего ориентирования снимка.

В связи с тем, что уравнения (1.5.2) нелинейные, решение системы уравнений непосредственно достаточно сложно, поэтому систему уравнений (1.5.2) решают методом приближений.

Для этого уравнения (1.5.2) приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок.

. (1.5.3)

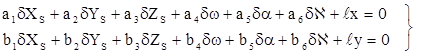
В уравнениях (1.5.3):

dXs, … ,dÀ — поправки к приближенным значениям неизвестных элементов внешнего ориентирования снимка Xs 0 ,…,À 0 ;

a_i, b_i – частные производные от уравнений (1.5.2) по соответствующим аргументам (например, коэффициент а₄ является частной производной от первого уравнения (1.5.2) по аргументу w,то есть );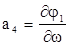

ℓх, ℓу – свободные члены.

Значения коэффициентов уравнений (1.5.3) a_i, b_i вычисляются по известным значениям координат точек снимка и местности х,у и X,Y,Z, известным значениям элементов внутреннего ориентирования снимка f,x₀,y₀ и приближенным значениям неизвестных Xs 0 ,…,À 0 .

Свободные члены ℓх, ℓу вычисляются по формулам (1.5.2) таким же образом.

В результате решения системы уравнений поправок (1.5.3) находят поправки к приближенным значениям неизвестных и вычисляют уточненные значения неизвестных.

По уточненным значениям неизвестных повторно составляют уравнения поправок (1.5.3) и решают полученную систему уравнений.

Решения повторяют до тех пор, пока величины поправок, найденные в результате решения, не станут пренебрежимо малыми.

В случае если на снимке измерено более трех изображений опорных точек, то для каждой точки составляют уравнения поправок вида:

; (1.5.4)

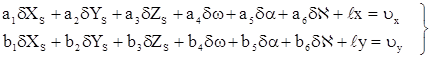
Решение полученной системы уравнений (1.5.4) производят методом приближений, по методу наименьших квадратов (под условием V T V = min).

Источник

47 Определение элементов ориентирования снимка

Решение прямой фотограмметрической засечки возможно при условии, что элементы ориентирования снимка известны.

Элементы внутреннего ориентирования, как правило, извест¬ны. Они определяются при калибровке АФА с точностью 0,001 мм и записываются в его паспорт.

Элементы внешнего ориентирования снимка можно опреде¬лить различными способами. Их делят на две группы.

В первую группу входят способы определения элементов внешнего ориентирования снимков в полете с помощью специальных приборов. Например, координаты центров проекций находят по показаниям GPS-приемников, установленных на борту летатель¬ного аппарата. Угловые элементы внешнего ориентирования (а, со) определяют с помощью инерциальных систем навигации.

Во вторую группу входят способы для определения элементов внешнего ориентирования снимков по опорным точкам.

Опорными точками называют точки с известными геодезичес¬кими координатами. Определение элементов внешнего ориенти¬рования снимков с использованием опорных точек называют об¬ратной фотограмметрической засечкой или задачей по ориентиро¬ванию снимка, которую решают аналитически с использованием уже известных из раздела 7.4 уравнений связи координат точек снимка и местности:….

В правых частях уравнений (7.2) содержатся все шесть искомых элементов внешнего ориентирования снимка. Для одной опорной точки с геодезическими координатами (ХТ, F, Z1″) и измеренными координатами (х, у) ее изображения на снимке можно составить два независимых уравнения вида (7.2) с шестью неизвестными ве¬личинами — XTS, Y§, ZJ, а, со, к. Чтобы однозначно определить все шесть элементов внешнего ориентирования, необходимо объединить в систему не менее шести независимых уравнений, со¬держащих искомые элементы. Для этого требуется не менее трех планово-высотных опорных точек.

Для решения обратной фотограмметрической засечки с конт¬ролем используют четыре опорные точки и более, расположенные по углам рабочей площади снимка. Увеличение числа опорных то¬чек позволяет также отбраковывать грубые измерения.

Билет № 48. Способы построения цифровых моделей рельефа и их применение. Цифровая модель рельефа представляет собой плавную поверхность, проходящую через точки с известными высотами, описываемую некоторой функцией F, определяющей зависимость отметки точки местности от ее плановых координат: Z= F(Х, У ). Отметки пикетов, используемых для построения ЦМР, могут быть получены в результате полевых геодезических измерений, по топографическим картам, путем стереофотограмметрической обработки снимков. В зависимости от расположения пикетов различают регулярные, полурегулярные и структурные ЦМР. Наиболее широкое применение получили регулярные ЦМР, в которых пикетные точки, которые располагаются в узлах сетки квадратов, прямоугольников и равносторонних треугольников. Однако построение регулярных ЦМР может повлечь потерю информации о рельефе местности. Это вызвано тем, что характерные точки рельефа – вершины холмов, дно котловин и др. могут оказаться между узлами сетки и не отобразиться на ЦМР. Структурные ЦМР наиболее точно описывают описывают рельеф, поскольку их пикетные точки выбирают в характерных местах рельефа. При проектировании линейных сооружений создают полурегулярные ЦМР. В этих моделях пикетные точки располагают на поперечниках к трассе в характерных местах рельефа или на определенном расстоянии друг от друга. Цифровая модель рельефа позволяет получить отметку любой точки местности с определенной точностью, что необходимо при цифровой фотограмметрической обработке одиночных снимков.

.Билет № 49. Тех. ср-ва, используемые для ФГМ обработки снимков. Программное обеспечение. Устройства ввода и вывода. Основой технических средств являются компьютеры, важнейшими характеристиками которых с точки зрения потребителя можно считать тактовую частоту процессора, емкость жесткого диска и его быстродействие Цифровые технологии фотограмметрической обработки снимков предусматривают использование специального комплекса технических средств — цифровых фотограмметрических рабочих станций (ЦФРС), включающих устройства ввода-вывода изображений и вычислительный комплекс, который производится на персональных компьютерах с последними поколениями прцессоров Intel Поскольку исходным материалом для цифровых технологий в большинстве случаев остаются аэрофотоснимки, их необходимо преобразовать в цифровой вид — цифровать. Цифрование можно проводить в двух вариантах: растровом и векторном. Получение растрового изображения — поэлементная запись исходного изображения в трехмерном коде: плановые координаты точки на изображении (х, у) и закодированная оптическая плотность или цвет этой точки. Техническими средствами, осуществляющими получение растрового изображения, являются сканеры, сам процесс называют сканированием. В зависимости от конструкции и принципа действия различают планшетные, барабанные и протяжные (роликовые) сканеры. Векторизацию можно производить вручную с помощью дигитайзеров( устройства для ручного ввода графической информации), а также на экране монитора в ручном, полуавтоматическом или автоматическом режимах. Основные технические характеристики сканеров: позиционная точность сканера во многом зависит от его конструкции и измеряется в процентах от длины отрезка, линейная разрешающая способность(показывает размер элементарной площадки сканирования число пикселей в дюйме изображения), энергетическая разрешающая способность сканера зависит от вида приемника излучения. У цветных сканеров еще и глубина цвета, ктотрая характеризует максимальное число цветов, различаемых сканером, и измеряется в битах на точку растрового изображения. Устройства, позволяющие вывести на печать цифровую информацию, называют плоттерами или принтерами. Плоттеры выводят изображение на широкоформатные материалы (бумагу, пленку, кальку). Для вывода малоформатных фотоизображений используют принтеры. Программное обеспечение.Внедрение способов цифровой фотограмметрии позволяет выполнить весь процесс фотограмметрической обработки снимков не только немногочисленными специализированными организациями, но и специалистам различных прикладных областей: землеустроителям, почвоведам, кадастровикам. Фотограмметрическое программное обеспечение имеет свои специфические особенности. Это прежде всего необходимость работы с огромными по объему файлами и пространственная привязанность информации. Для работы с большими объемами файлов используются специальные форматы данных: иерархические, блоковые и др. Иерархическая структура представляет собой пирамидные слои. Сблокированная структура (совокупность блоков) — небольшие квадратные участки изображения с прямым доступом к каждому из них. Современные пакеты программ обработки снимков разработаны таким образом, чтобы хранить не результаты обработки, а исходные снимки и алгоритмы, позволяющие в нужный момент получить нужный результат. Фотограмметрическое программное обеспечение подразделяют на два больших класса: программы обработки одиночных снимков и программы стереофотограмметрической обработки.

Источник

§ 6 Элементы внешнего ориентирования снимка

Элементы ориентирования снимка определяют положение его от­носительно пространственной прямоугольной системы координат OXYZ в момент фотографирования.

Различают элементы внутреннего и внешнего ориентирования снимка.

Элементы внутреннего ориентирования позволяют найти поло­жение центра проекции относительно снимка. Как известно из предыдущего параграфа, к ним относятся координаты главной точки снимка и фокусное расстояние фотокамеры. Зная элементы внутреннего ориентирования, можно восстановить по снимку связку проектирующих лучей, существовавшую в момент фото­графирования.

Элементы внешнего ориентирования определяют положение связки относительно пространственной прямоугольной системы координат в момент фотографирования.

Для аэроснимков используют две системы элементов внеш­него ориентирования.

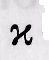
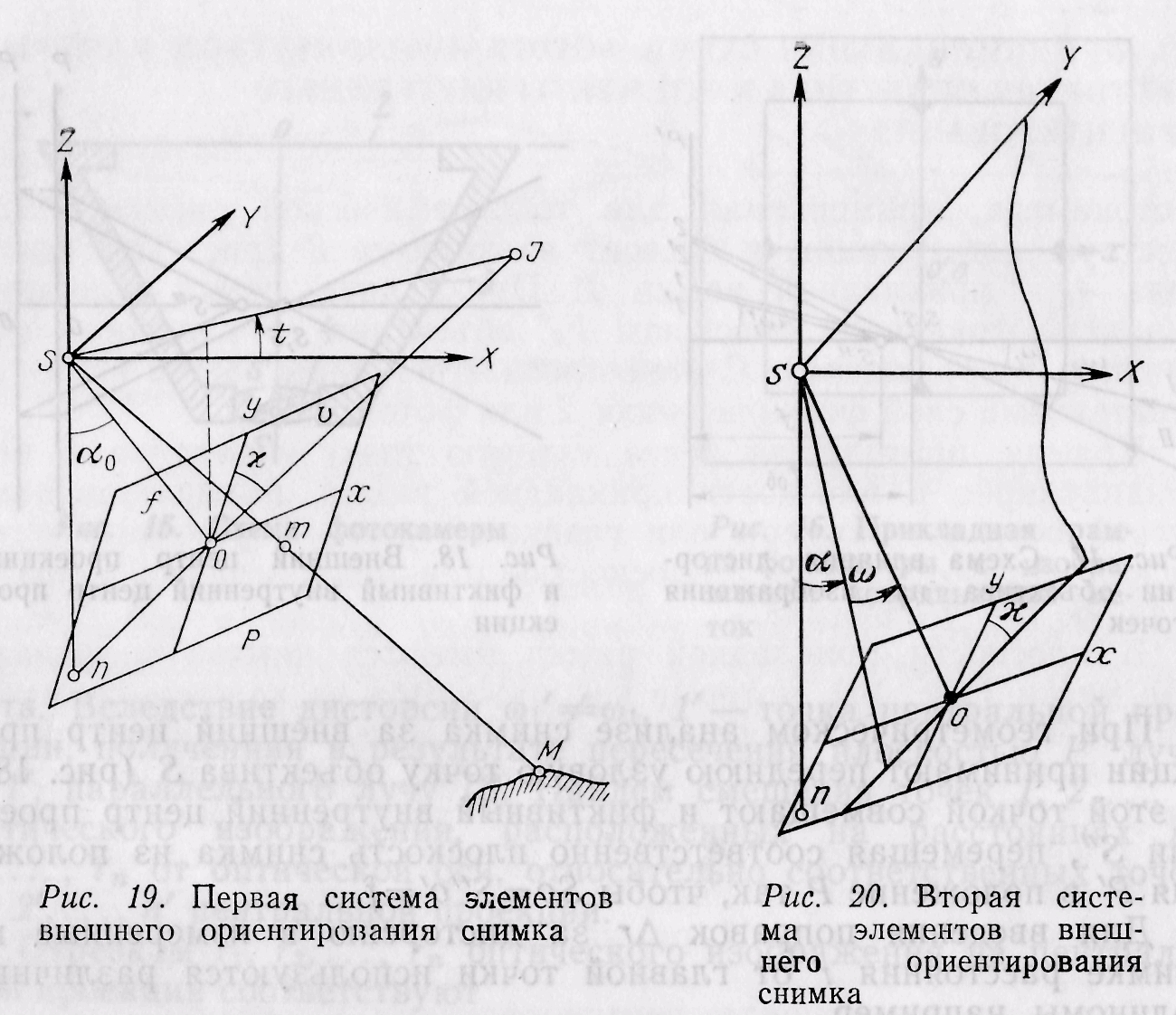
Первая система (рис. 19) содержит: X_S,, Y_S,, Z_S— координаты точки фотографирования, в которой находился центр проекции S; α_о — угол наклона снимка или угол отклонения оптической оси фотокамеры от отвесной линии; t — дирекционный угол оптиче­ской оси фотокамеры — угол между осью SX и проекцией главного луча на плоскость SXY; — угол поворота снимка (на снимке угол между главной вертикалью и осью оу). Оси SX, SY и SZ параллельны соответствующим осям системы координат OXYZ.

Вторая система элементов внешнего ориентирования (рис. 20) включает: X_S,, Y_S,, Z_S — координаты точки фотографирования; α — продольный угол наклона снимка, т. е. угол между осью SZ и проекцией главного луча на плоскость SXZ; ω— поперечный угол наклона снимка, составленный главным лучом с плоскостью SXZ; — угол поворота снимка, т. е. угол на снимке между осью оу и следом плоскости, проходящей через главный луч и ось SY.

Непрямолинейность маршрутов, характеризующаяся отноше­нием стрелки прогиба к длине маршрута, не должна превышать 2 % при съемке в масштабах мельче 1 : 5000 и с высот 750 м и выше, а также 3 % при съемке в масштабе 1 :5000 и крупнее и с высот ниже 750 м.

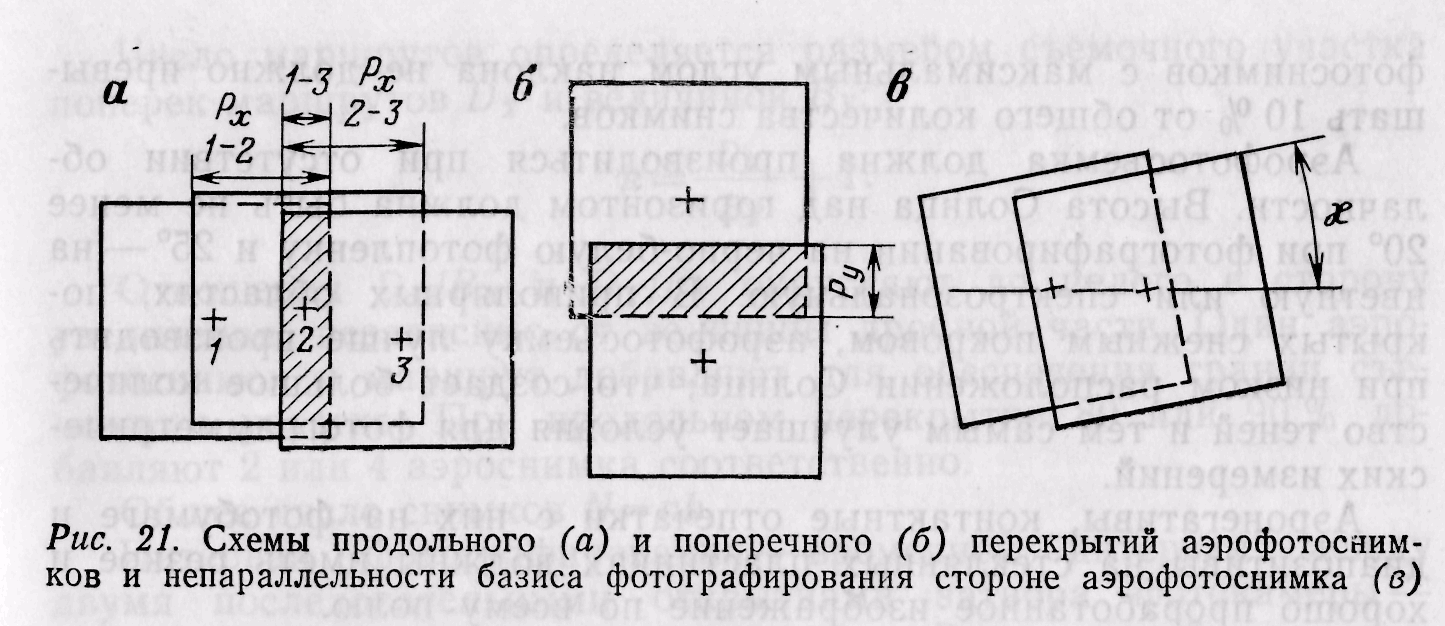
Продольное перекрытие Р_х аэрофотоснимков должно быть в среднем 60% (минимальное перекрытие 56%), что обеспечи­вает наличие тройного продольного перекрытия не менее 12 % (рис. 21, а). Перекрытие трех последовательных аэрофотосним­ков является обязательным, так как оно определяет величину перекрытия между соседними стереопарами. В пределах этого перекрытия набирают связующие точки, обеспечивающие пере­дачу координат с одной стереопары на другую.

В зависимости от целей аэрофотосъемки и используемых тех­нических средств продольное перекрытие может устанавливаться в 80 и 90% с колебанием в пределах 3—5%. В этих случаях, если взять аэроснимки через один (Р_ж = 80%) или три (Р_ж= = 90%), то получим соответственно два или четыре маршрута с Р_ж = 6О%, что позволяет провести независимые измерения по каждому из маршрутов.

Поперечное перекрытие Р_у аэрофотоснимков (рис. 21, б) из смежных маршрутов должно быть в среднем 30—40 % при ми­нимальном значении 20 % и максимальном, не превышающем среднего на 10—20 %.

В поперечном перекрытии намечают точки полевой привязки аэрофотоснимков, связующие точки для передачи координат с од­ного маршрута на другой, точки фотограмметрического сгущения. Для повышения точности построения сетей блочной фототриангу­ляции выполняют аэрофотосъемку с Р_у = 60 %.

Непараллельность базиса фотографирования стороне аэро­фотоснимка (рис. 21, в), так называемая «елочка», не должна превышать 5° для фокусных расстояний фотокамер 100 мм и ме­нее, 10—12° —для f=200—350 мм и 14° —для f=500 мм.

Углы наклона аэрофотоснимков при съемке без стабилизации не должны превышать 3°, а со стабилизацией—1°. Число аэрофотоснимков с максимальным углом наклона не должно превы­шать 10 % от общего количества снимков.

Аэрофотосъемка должна производиться при отсутствии об­лачности. Высота Солнца над горизонтом должна быть не менее 20° при фотографировании на черно-белую фотопленку и 25° — на цветную или спектрозональную. В приполярных областях, по­крытых снежным покровом, аэрофотосъемку лучше производить при низком расположении Солнца, что создает большое количе­ство теней и тем самым улучшает условия для фотограмметриче­ских измерений.

Аэронегативы, контактные отпечатки с них на фотобумаге и диапозитивы на стеклянных пластинках должны иметь резкое и хорошо проработанное изображение по всему полю.

Источник