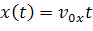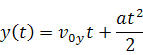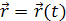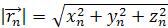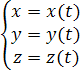Способы описания системы система отсчета

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта .

Движущиеся тела изменяют своё положение относительно других тел в пространстве с течением времени. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Можно показать, что одно и то же тело при одном и том же движении может одновременно по-разному перемещаться относительно разных тел.

Таким образом говорить о том, что какое-то тело движется, можно лишь тогда, когда ясно, относительно какого другого тела — тела отсчета , изменилось его положение.

Абсолютная система отсчёта

Часто в физике какую-то СО считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.

С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Например, физики XIX в. считали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа Абсолютной Системой Отсчета (АСО). В современных представлениях никакой системы отсчёта, выделенной именно таким способом, не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — локальная пространственно-временная инвариантность — является одним из проверяемых оснований физики.

Иногда абсолютной системой отсчета называют систему, связанную с реликтовым излучением, то есть инерциальную систему отсчета, в которой реликтовое излучение не имеет дипольной анизотропии.

Источник

Способы описания движения. Система отсчёта

Цели урока:

обучающая: Понять, каким образом можно описать движение тела. Познакомиться с таким важным понятием, как система отсчёта.

развивающая: развитие умения применять полученные знания на практике, видеть, как законы физики проявляются в повседневной жизни и как они могут быть использованы людьми.

воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся, повышать мотивацию к изучению физики.

Методы:

контролирующий — решение задач с использованием наглядных примеров

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

Мы приступаем к изучению механических явлений. Эти явления наиболее очевидные, и вы сталкиваетесь с ними каждый день. Вы легко можете описать любое движение, которое видите, используя обыденные фразы и наблюдения. Но как описать движение научно? Сегодня мы поговорим о том, как с точки зрения физики можно описать движение.

3. Объяснение нового материала.

В первую очередь, нужно понять, что любое движение относительно. А, значит, нужна какая-то точка отсчёта. Более того, нужно организовать систему, которая позволит нам описать движение математически. Такая система называется системой отсчёта. Очевидно, что описание движения будет зависеть от того, что мы примем за начальную точку, то есть, за точку отсчёта.

Всем известно, что барон Мюнхгаузен утверждал, что может летать на ядре. На этом замечательном примере, мы покажем, каким образом можно описать движение любого тела.

Простой пример относительности движения — это рассмотрение движения корабля с точки зрения наблюдателя на берегу и с точки зрения наблюдателя на корабле. Этот пример отлично демонстрирует насколько важно понимать, какую систему отсчета мы выбираем для описания того или иного движения.

Ещё одним хорошим примером является движение трёх объектов относительно друг друга. Нетрудно догадаться, что рассматривая одно и то же движение, относительно разных объектов, мы получим разное описание.

4. Решение задач.

Ну и конечно, необходимо рассмотреть практическое применение полученных знаний, то есть, решение задач.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

Источник

Способы описания системы система отсчета

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Способы описания движения. Система отсчета

Урок 3. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Способы описания движения. Система отсчета»

Сегодня мы рассмотрим наиболее распространенные способы описания движения и более подробно остановимся на понятии системы отсчёта. Напомним, что для описания движения материальной точки нужно научиться рассчитывать положение точки в любой момент времени, относительно выбранного тела отсчета.

Например, если мы задаём положение точки в системе координат, то каждая координата будет зависеть от времени. То есть, чтобы описать движение точки нужно найти функцию зависимости каждой координаты от времени.

Для примера возьмем подвиг незабвенного барона Мюнхгаузена, который утверждал, что может летать на ядре. Если учесть большое расстояние, которое пролетает ядро, то Мюнхгаузена можно считать за точку. Пушка будет являться телом отсчёта, то есть, началом координат. Положение барона можно описать с помощью двух координат, поскольку он двигается только в одной плоскости.

Тогда, зависимости координат х и у будут описываться уравнениями:

Эти уравнения называются кинематическими уравнениями движения точки.

Линия, вдоль которой движется точка в пространстве, называется траекторией.

Движение может быть разным, и траектория может быть сколь угодно сложной. Движение называется прямолинейным, если траектория является прямой линией.

Если же траектория представляет собой кривую, то это движение криволинейное.

Другой способ описания движения — это векторный способ. На прошлом уроке мы познакомились с тем, как задавать положение точки с помощью радиус-вектора. Если точка двигается, то с течением времени, радиус вектор может изменять длину и направление. Таким образом, радиус-вектор являться функцией зависимости от времени:

Поскольку радиус-вектор определяется с помощью координат, то одно векторное уравнение эквивалентно трём скалярным уравнениям:

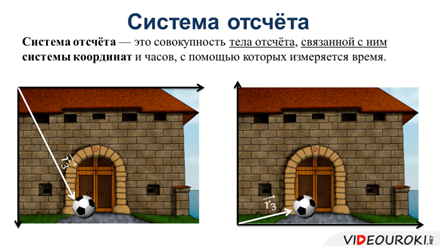
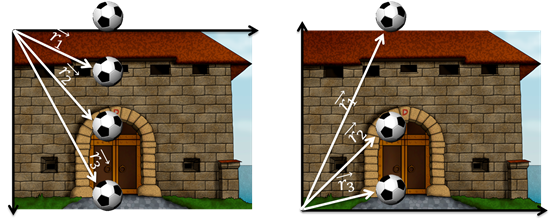
Как мы знаем, системой отсчёта называется совокупность тела отсчёта и связанной с ним системы координат и часов, с помощью которых измеряется время. В различных системах отсчёта движение одного и того же тела может быть описано по-разному. Например, если сбросить мяч с крыши дома, то в системе отсчёта, связанной с крышей, длина радиус-вектора будет увеличиваться. Но в системе отсчёта связанной с поверхностью Земли, длина радиус-вектора будет уменьшаться.

Главное запомнить следующее: если выбрали тело отсчета, то все наблюдения, вычисления и уравнения должны быть связаны именно с этим телом отсчёта, как с началом координат.

Например, в каюте корабля все предметы остаются неподвижны, относительно корабля. Но, вместе с этим, все эти предметы двигаются относительно поверхности земли.

Таким образом, в системе отсчета, связанной с кораблем, координаты тел, находящихся в каюте, будут заданы постоянными величинами. В системе отсчёта, связанной с поверхностью земли, координаты будут задаваться в соответствии со скоростью движения корабля. Если мы предположим, что корабль двигается равномерно и прямолинейно, то меняться будет только одна координата. Если же мы предположим, что корабль покачивается на волнах, то координата зет будет задана периодичной функцией.

Примеры решения задач.

Задача 1. Самолёт летит в одной плоскости. В начальный момент времени самолёт находится на высоте 1000 м и на расстоянии 5 км от аэродрома. Постройте соответствующую систему координат и отметьте на ней самолёт в начальный момент времени.

Давайте выполним несколько упражнений. Допустим, самолёт летит в одной плоскости. В начальный момент времени самолет находится на высоте 1000 метров и на расстоянии 5 километров от аэродрома. Постройте соответствующую систему координат и отметьте на ней самолет в начальный момент времени.

Итак, очевидно, что телом отсчёта в данном случае является аэродром.

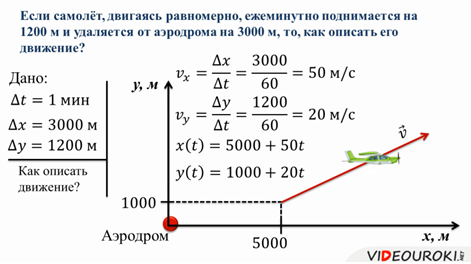
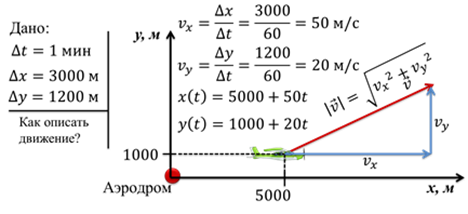
Задача 2. Если самолёт, двигаясь равномерно, ежеминутно поднимается на 1200 метров и удаляется от аэродрома на 3000 метров, то, как описать его движение?

Из формулировки этого вопроса мы можем извлечь следующее: в одинаковые промежутки времени, равные 1 мин, горизонтальное перемещение самолёта составляет 3000 метров, а вертикальное — 1200 метров.

Обратите внимание, что реальная скорость самолёта направлена так, что самолёт одновременно удаляется от аэродрома и в горизонтальном, и в вертикальном направлении. Поэтому, скорости, которые мы нашли — это проекции вектора скорости на оси х и у.

Источник