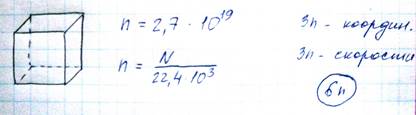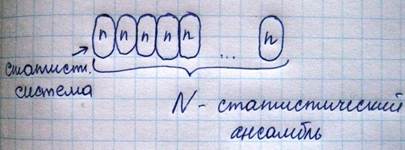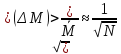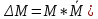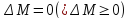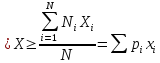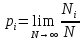Статистический и термодинамический методы описания систем многих частиц.
Все тела состоят из атомов и молекул. Известно также строение атомов и молекул. Поэтому моделью материального тела является совокупность атомов и молекул, взаимодействующих между собой по некоторым законам и соответственным образом движущихся. Сами атомы и молекулы в зависимости от характера рассматриваемых явлений принимаются как материальные точки, либо как твердые тела, либо учитывается их внутреннее строение и взаимодействие между собой.
Квантовая механика позволяет полностью изучить строение атомов и молекул, и поэтому все их свойства могут считаться известными, а поэтому известными также являются и характеристики соответствующих моделей. Движение атомов и молекул в зависимости от характера процессов могут рассматриваться либо чисто классическим, то есть так же как рассматривается движение материальных точек и твердых тел, в других случаях необходимо учитывать квантовые закономерности, характерные для движения микрочастиц, поэтому можно сказать, что моделью материального тела является совокупность атомов и молекул, свойства, законы движения и взаимодействия которых известно.
Массы атомов и молекул.
В молекулярной физике массы атомов и молекул принято характеризовать не их абсолютными значениями, выраженными в килограммах, а относительными безразмерными единицами (Mr – относительная молекулярная масса, Ma – относительная атомная масса). В качестве единичной атомной массы берется mu=1,66*10 -27 кг берется 1/12 массы изотопа углерода.
Абсолютные массы атомов варьируются 10 -27 -10 -25 кг.
В молекулярной физике количество вещества принято характеризовать числом его структурных элементов, выражаемым в молях. Моль любого вещества равняется количеству? Рассматриваемой системы, которые содержат столько же структурных элементов (атомов), сколько атомов содержится в 0,012 кг 12 С. Это количество называется число Авогадро Na.
Na=0,012кг/12mu=10 -3 /1,66*10 -27 =6,02*10 23 моль -1 .
Кроме этого в молекулярной физике используется также молярная масса, которая представляет собой массу 1 моль вещества. (Na=10 -3 / mu)
Число молей структурных элементов ν=n/Na (H2, 2, M=2*10 -3 кг)
Агрегатное состояние вещества
Изучение взаимодействия между атомами и молекулами показало, что на сравнительно больших расстояниях между ними действует сила притяжения, тогда как на малых расстояниях — силы отталкивания. Эти силы являются электромагнитными. Существование сил отталкивания также есть просто констатация факта, что сами атомы и молекулы обладают каким-то объемом и препятствуют другим атомам и молекулам занять их объем. Все атомы и молекулы находятся в состоянии движения, и, следовательно, обладают определенным запасом кинетической энергии. Очевидно, что силы притяжения стремится связать атомы и молекулы в единое целое, но наличие кинетической энергии препятствует этой тенденции. Если суммарная кинетическая энергия атомов и молекул много больше суммарной потенциальной энергии их взаимного притяжения (по абсолютной величине, поскольку суммарная потенциальная энергия отрицательна), то вещество – газообразное, если много меньше — в твердом состоянии. В случае примерного равенства – жидкое состояние. Поскольку газообразное состояние вещества реализуется в результате полного подавления тенденции атомов и молекул к притяжению, то вещество не сохраняет ни формы, ни объема. То есть предоставленное самому себе заполняет собой все пространство. Картина движения молекул газа выглядит так: большую часть времени молекулы движутся прямолинейно, до тех пор пока в некоторой области пространства она траекторию движении в результате столкновения с другой молекулой. Расстояние, которое проходит молекула между столкновениями в сотни и тысячи раз больше самой молекулы. Это расстояние называется длина свободного пробега.
В твердых телах молекулы и атомы сильно сцеплены друг с другом, поэтому вещество сохраняет и форму и объем. При деформации твердого тела (изменение формы или объема) возникают значительные силы, стремящиеся вернуть тело в исходное состояние. Молекулы и атомы в твердом теле располагаются в вполне определенных местах, образую кристаллическую решетку. Атомы колеблются около некоторых средних положений – узлы кристаллической решетки — и покидать небольшую область вокруг узлов они не могут. Линии, вдоль которых атомы совершают свои колебания и амплитуды, меняются, но за гораздо большее время по сравнению с периодом своих колебаний.
В жидкостях, которые характеризуются тем, что вещество стремится сохранить объем, но не сохраняет форму. Жидкость всегда принимает ту форму, которая соответствует действующим на нее силам. Молекулы жидкости находятся достаточно близко друг к другу, как бы соприкасаясь, однако их взаимное расположение не фиксировано, то есть они, сравнительно медленно меняют свои положения относительно друг друга.
Иногда молекулы соединяются в комплексы (агрегаты), состоящие из большого числа молекул, причем расположение этих комплексов определенным образом упорядочено. В этом случае жидкость приобретает некоторые свойства, характерные для твердых тел. Такие жидкости называются жидкие кристаллы. В настоящее время сравнительно хорошо разработана теория твердого, газообразного состояния, тогда как жидкое состояние не до конца понято.
Модель идеального газа
Наиболее простой моделью системы многих частиц является модель идеального газа. Идеальный газ – это газ, состоящий из точечных материальных частиц с конечной массой, между которыми отсутствуют силы, действующие на расстоянии и которые сталкиваются между собой по законам соударения шаров, то есть они испытывают только лобовые столкновения, в результате которых направление скорости изменяет свой знак. Наиболее близко этим свойствам отвечают разреженные газы.
При изучении систем многих частиц информация должна иметь обобщенный характер и относиться не к отдельным частицам, а к совокупности большого числа частиц. Соответственно, понятия также должны относиться не к отдельным частицам, а к большим совокупностям. Новая форма информации и новые понятия требуют специального метода рассмотрения, называемого статистическим методом. Статистические методы используются также и для описания поведения систем с небольшим числом степеней свободы, если в поведении этих систем существенны квантовые эффекты, которые являются статистически .
Систему многих частиц можно рассматривать и по-иному не интересуясь ее внутренней структурой. При таком подходе нужно использовать понятия и физические величины, относящиеся к системе в целом. Например, модель идеального газа в состоянии равновесия при таком подходе полностью может быть описана тремя характеристиками T,V,p. Экспериментальные исследования призваны исследовать взаимосвязь между этими параметрами, а теория должна строиться на некоторых общих положениях (ЗСЭ) и объяснять эти связи. Такая теория по своему характеру является феноменологической. Феноменологическая теория не интересуется внутренними механизмами процессов, определяющих поведение системы. И такой метод изучения называется термодинамический метод. Термодинамический метод характеризуется своей общностью, он позволяет изучать явления без знания внутренних механизмов. Статистический метод позволяет понять суть явлений, установить связь поведения системы в целом с поведением и свойствами отдельных её частиц.
Макро и микроскопические состояния системы многих частиц
Системой называется конечная область пространства вместе с находящимися в ней физическими объектами исследования. Граница системы может быть как материальной (стенка сосуда) так и воображаемой. Граница может быть подвижной или неподвижной, проницаемой или непроницаемой для вещества, через нее возможен или невозможен транспорт энергии. Система также характеризуется физическими или химическими свойствами вещества, заключенными в ней.
Пусть в некотором объеме V находится идеальный газ. Предположим, что удары частиц о стенки сосуда являются абсолютно упругими и будем считать, что масса сосуда очень велика. Вследствие этого состояние движения частиц из-за ударов не изменяется. Таким образом, газ, заключенный в этом объеме, не обменивается энергией с окружающими материальными телами и все, что с ним может произойти, происходит вследствие внутреннего взаимодействия. По прошествии достаточного промежутка времени, в течение которого система предоставлена сама себе, состояние газа станет стационарным и не будет изменяться с течением времени. Таким образом, стационарное состояние газа означает, что температура и давление во всех точках занимаемого объема будут одинаковые и не будут изменяться. Состояние газа, характеризуемое его давлением, температурой и объемом называется макроскопическим состоянием. Стационарное состояние газа, находящегося в изолированном от среды объеме называется равновесным.
Наиболее полная информация о состоянии газа в констатации местоположений (координат) скоростей всех его частиц.
Состояние газа, характеризуемое положениями и скоростями, называется микросостоянием. Микросостояние характеризуется тремя величинами P, V, T, которые в стационарном состоянии постоянны, однако частицы газа в стационарном состоянии непрерывно движутся, то есть его микросостояние непрерывно меняется. Одному и тому же макросостоянию соответствует бесчисленное множество микросостояний.
Задача статистической физики заключается в исследовании связи между микро — и макросостояниями системы.
Одно и то же макросостояние осуществляется в большом числе систем ансамбля, находящихся в различных. Микроканонический ансамбль состоит из одинаковых изолированных систем с одинаковой энергией. При описании микросостояния каждой частице выделяется в пространстве координаты-импульсы. причем объем в фазовом пространстве может быть вычислен:
Постулат равновероятности: все микросостояния равновероятны.
Эрготическая гипотеза: средний по ансамблю равен среднему по времени.
12.09.2012
Система не знает, какое макросостояние является наиболее вероятным. Она непрерывно переходит из одного микросостояния в другое не отдавая предпочтения какому-либо из них. Однако подавляющее число переходов осуществляется в направлении равновесного состояния. В результате чего можно сделать вывод, что полностью хаотические переходы из одного микросостояния в другое создают упорядоченное движение системы к равновесному состоянию.
Число микросостояний, посредством которых реализуется данное макросостояние, называется термодинамическая вероятность макросостояний. Это число очень велико.
Вероятностью макросостояний системы называется отношение его термодинамической вероятности к полному числу возможных микросостояний. Оно меньше-равно 1.
Наиболее вероятным состоянием изолированной системы предоставленной самой себе является равновесное состояние.
Источник
Оглавление
Статистическая физика 3
Динамический подход и его бесперспективность 3
Статистический метод описания коллектива частиц 3
Макро- и микросостояния 5
Энтропия и ее статистический смысл 5
Термодинамический способ описания коллектива частиц 6
Внутренняя энергия системы 6
Полная статистическая функция распределения 7
Вырожденные и невырожденные коллективы частиц 9
Функция распределения Максвелла-Больцмана 10
Функция распределения Максвелла по абсолютным значениям скоростей 11
Зависимость распределения Максвелла от температуры 11
Формула Максвелла в приведенном виде 12
Экспериментальная проверка распределения Максвелла. Опыт Штерна 12
Средняя энергия молекул идеального газа 13
Основное уравнение МКТ 13
Средняя энергия молекул и МК смысл абсолютной температуры 14
Закон равномерного распределения энергии молекул по степеням свободы. 15
Закон равнораспределения 15
Распределение молекул в поле сил тяготения 16
Распределение Больцмана 16
Опыт Перрена по определению числа Авогадро 16
Квантовые статистики 17
Функция Ферми-Дирака 18
Первое начало термодинамики: 19
Уравнение Менделеева – Клапейрона 19
Работа газа при изменении его объема 19
Применение первого начала термодинамики к изопроцессам. Изопроцессы. 21
Адиабатический процесс. 22
Круговые процессы 23
Второе начало термодинамики 25
Тепловой двигатель 25
Явление переноса 27
Фазовые переходы 30
Фазовые переходы 31
Квантовая механика 33
Опыт Резерфорда. Ядерная модель атома 33
Теория Бора для водородоподобных систем 34
Первый постулат Бора: 34
Второй постулат Бора: 34
Обобщенная сериальная формула Бальмера 34
Волна Де Бройля 34
Гипотеза Де Бройля 34
Принцип неопределенности Гейзенберга 35
Уравнение Шредингера 35
Описание движения свободной частицы 36
Частица в бесконечно глубокой одномерной потенциальной яме 36
Уровни энергии частицы в потенциальной яме 37
Потенциальный барьер 39
Гармонический осциллятор 39
Решение уравнения Шредингера для водородоподобного атома 40
Энергия ионизации атома водорода 40
Спин электрона 42
Распределение электрона в атоме 42
Статистическая физика Динамический подход и его бесперспективность
Реальное вещество состоит из большого числа частиц – молекул. Например в 12 граммах изотопа углерода содержится 
Можно было бы написать для каждой молекулы уравнение движения:
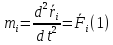
На самом деле получилось Nуравнений (т.к.x,y,z)
Их решить совместно практически невозможно.
Статистический метод описания коллектива частиц
Чем больше членов коллектива, тем точнее статистические предсказания
Для системы из Nчастиц относительного отклонения наблюдаемой статистической величины (М)от ее среднего значения (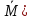
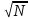
Отклонения от среднего значения называются Флуктуациями(
Среднее арифметическое величины
Поэтому в качестве меры флуктуации берут среднюю квадратичную флуктуацию
Среднее значение измеряемой величины Х равно
Ni– число измерений, которые дали результатыxi

Величина Ni/N– относительная частота появления результатаxi
В случае, когда Nвелико,
Pi– вероятность появления результата хi
Cледуя правилам статистического усреднения имеем:
Источник