- Способы описания геометрических объектов векторная графика
- Полигональные модели
- Воксельные модели
- Поверхности свободных форм (функциональные модели)
- Системы координат: мировая, объектная, наблюдателя и экранная
- Однородные координаты. Задание геометрических преобразований в однородных координатах с помощью матриц
Способы описания геометрических объектов векторная графика
Под геометрическими примитивами понимают тот базовый набор геометрических фигур, который лежит в основе всех графических построений, причем эти фигуры должны образовывать «базис» в том смысле, что ни один из этих объектов нельзя построить через другие. Однако вопрос о том, что включать в набор геометрических примитивов, нельзя считать окончательно решенным в компьютерной графике. Например, количество примитивов можно свести к некоему минимуму, без которого нельзя обойтись, и этот минимум сводится к аппаратно реализованным графическим объектам. В этом случае базисный набор ограничивается отрезком, многоугольником и набором литер (символов).
Другая точка зрения состоит в том, что в набор примитивов необходимо включить гладкие кривые различного рода (окружности, эллипсы, кривые Безье), некоторые классы поверхностей и даже сплошные геометрические тела. В качестве трехмерных геометрических примитивов в таком случае предлагаются пространственные кривые, параллелепипеды, пирамиды, эллипсоиды. Но если такой расширенный набор примитивов связан с аппаратной реализацией, то возникает проблема перенесения программных приложений с одного компьютера на другой, поскольку такая аппаратная поддержка существует далеко не на всех графических станциях. Кроме того, при создании трехмерных геометрических примитивов программисты сталкиваются с проблемой их математического описания, а также разработки методов манипулирования такими объектами, поскольку те типы объектов, которые не попали в список базовых, надо уметь приближать с помощью этих примитивов.
Во многих случаях для аппроксимации сложных поверхностей используются многогранники, но форма граней может быть различной. Пространственный многоугольник с числом вершин больше трех не всегда бывает плоским, а в этом случае алгоритмы изображения многогранников могут привести к некорректному результату. Поэтому программист должен сам позаботиться о том, чтобы многогранник был описан правильно. В этом случае оптимальным выходом из положения является использование треугольников, поскольку треугольник всегда является плоским. В современной графике это, пожалуй, самый распространенный подход.
Но существует и альтернативное направление, которое называется конструктивной геометрией тел. В системах, использующих этот подход, объекты строятся из объемных примитивов с использованием теоретико- множественных операций (объединение, пересечение).
Любая графическая библиотека определяет свой набор примитивов. Так, например, широко распространенная интерактивная система трехмерной графики OpenGL включает в список своих примитивов точки (вершины), отрезки, ломаные, многоугольники (среди которых особо выделяются треугольники и четырехугольники), полосы (группы треугольников или четырехугольников с общими вершинами) и шрифты. Кроме того, в нее входят и некоторые геометрические тела: сфера, цилиндр, конус и др.
Понятно, что для изображения таких примитивов должны быть разработаны эффективные и надежные алгоритмы, поскольку они являются конструктивными элементами. Исторически сложилось так, что первые дисплеи были векторными, поэтому базовым примитивом был отрезок. Но, как уже было отмечено в первой главе нашего курса, самая первая интерактивная программа Sketchpad А.Сазерленда в качестве одного из примитивов имела прямоугольник, после чего этот объект уже традиционно входил в различные графические библиотеки.
Здесь мы рассмотрим такие примитивы, как вершина, отрезок, воксель и модели, строящиеся на их основе, а такжефункциональные модели.
Полигональные модели
Для этих пространственных моделей используются в качестве примитивов вершины (точки в пространстве), отрезки прямых (векторы), из которых строятся полилинии, полигоны и полигональные поверхности. Главным элементом описания является вершина, все остальные являются производными. В трехмерной декартовой системе координаты вершины определяются своими координатами (x,y,z), линия задается двумя вершинами, полилиния представляет собой незамкнутую ломаную линию, полигон — замкнутую ломаную линию. Полигон моделирует плоский объект и может описывать плоскую грань объемного объекта. Несколько граней составляют этот объект в виде полигональной поверхности — многогранник или незамкнутую поверхность («полигональная сетка»).
В современной компьютерной графике векторно-полигональная модель является наиболее распространенной. Она применяется в системах автоматизированного проектирования, компьютерных играх, тренажерах, ГИС, САПР и т. д. Достоинства этой модели заключаются в следующем:
- Удобство масштабирования объектов.
- Небольшой объем данных для описания простых поверхностей.
- Аппаратная поддержка многих операций.
К числу недостатков полигональных моделей можно отнести то, что алгоритмы визуализации выполнения топологических операций (например, построение сечений) довольно сложны. Кроме того, аппроксимация плоскими гранями приводит к значительной погрешности, особенно при моделировании поверхностей сложной формы.
Воксельные модели
Воксельная модель — это представление объектов в виде трехмерного массива объемных (кубических) элементов. Само название «воксель» составлено из двух слов: volume element. Так же как и пиксель, воксель имеет свои атрибуты (цвет, прозрачность и т. п.). Полная прозрачность вокселя означает пустоту в соответствующей точке объема. Чем больше вокселей в определенном объеме и меньше их размер, тем точнее моделируются трехмерные объекты.
Положительными чертами воксельной модели являются:
- Возможность представлять внутренность объекта, а не только внешний слой; простая процедура отображения объемных сцен.
- Простое выполнение топологических операций; например, чтобы показать сечение пространственного тела, достаточно воксели сделать прозрачными.
К ее недостаткам относятся:
- Большое количество информации, необходимое для представления объемных данных.
- Значительные затраты памяти, ограничивающие разрешающую способность, точность моделирования.
- Проблемы при увеличении или уменьшении изображения; например, с увеличением ухудшается разрешающая способность изображения.
Поверхности свободных форм (функциональные модели)
Характерной особенностью предлагаемого способа задания поверхностей является то, что основным примитивом здесь является поверхность второго порядка — квадрик. Он определяется с помощью вещественной непрерывной функции трех переменных 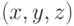
Свободная форма — это произвольная поверхность, обладающая свойствами гладкости, непрерывности и неразрывности. На базе квадриков строятся свободные формы, которые описывают функциональные модели. Свободная форма, построенная на этих принципах, имеет ряд достоинств, к которым, в первую очередь, надо отнести следующие:
- Легкая процедура расчета координат каждой точки.
- Небольшой объем информации для описания достаточно сложных форм.
- Возможность строить поверхности на основе скалярных данных без предварительной триангуляции.
Этот подход будет более подробно изложен в следующих главах.
В нашем курсе предполагается рассмотреть растровые алгоритмы для изображения таких геометрических примитивов, как отрезки, многоугольники, окружности и эллипсы. Но сначала мы займемся тем геометрическим аппаратом, который позволит адекватно описывать объекты в пространстве, работать с ними и формировать изображение.
Системы координат: мировая, объектная, наблюдателя и экранная
Одной из распространенных задач компьютерной графики является изображение двумерных графиков в некоторой системе координат. Эти графики предназначены для отображения зависимости между переменными, заданной с помощью функции. Например, во второй главе настоящего курса приведен ряд графиков, характеризующих восприятие света глазом человека. Чтобы получить такой график, прикладная программа должна описать различные выходные примитивы (точки, линии, цепочки символов ), указав их местоположение и размеры в прямоугольной системе координат. Единицы измерения, в которых задаются эти объекты, зависят от их природы: изменение температуры, например, можно отображать в градусах за час, перемещение тела в пространстве — в километрах в секунду, и т. д. Эти прикладные (или ориентированные на пользователя) координаты позволяют задавать объекты в двумерном или трехмерном мире пользователя, и их принято называть мировыми координатами.
Изображение трехмерных объектов сопряжено с целым рядом задач. Прежде всего надо помнить, что изображение является плоским, поэтому надо добиться адекватной передачи визуальных свойств предметов, дать достаточно наглядное представление о глубине. В дальнейшем группы трехмерных объектов, предназначенных для изображения, будем называть пространственной сценой, а ее двумерное изображение — образом.
Как и в случае с двумерными объектами, первым шагом построения является ввод информации об объектах. Сцена занимает какое-то определенное место в пространстве, а ее описание привязывается к трехмерной декартовой системе координат, связанной с нею, — объектной координатной системе. Координаты объектов, составляющих сцену, определяются на основе их реальных размеров и взаимного расположения. В зависимости от точки, из которой рассматривается сцена, можно получить множество различных ее образов. Если построено достаточно много таких образов, то по ним можно восстановить объемную структуру предмета. Выбор точки и направления зрения тоже можно описать математически, введя декартову систему координат наблюдателя, начало которой находится в точке обзора, а одна из осей совпадает с направлением зрения (рис. 4.3). Переход от объектных координат к координатам наблюдателя математически реализуется так, как это было описано в третьей главе. На этом этапе преобразований сохраняются реальные размеры объектов.
Видимый образ формируется на некоторой плоскости, которую в дальнейшем будем называть картинной плоскостью. Способы преобразования трехмерного объекта в двумерный образ ( проекции ) могут быть различными. Так или иначе, но полученный образ также должен быть описан в некоторой двумерной системе координат. В зависимости от способа его получения реальные размеры образа также могут быть различны. Различные виды проецирования будут подробно рассмотрены в последующих главах.
Поскольку нашей конечной целью является получение изображения на экране, то перенесение образа сопровождается изменением масштаба в соответствии с размерами экрана. Обычно началом координат в системе координат образа считается левый нижний угол листа с изображением. На экране дисплея начало координат традиционно находится в левом верхнем углу. Отображение рисунка с картинной плоскости на экран должно производиться с минимальным искажением пропорций, что само по себе вносит ограничение на область экрана, занимаемую рисунком. Изменение масштаба должно осуществляться с сохранением пропорций области (рис. 4.4).
Объекты в системе координат картинной плоскости задаются в каких- либо единицах измерения, причем масштаб одинаков по обеим осям координат. На экране единицей измерения является пиксель, который следует рассматривать как прямоугольный, поэтому масштабы по горизонтальной и вертикальной осям могут быть различны, что необходимо учитывать при задании коэффициентов масштабирования.
Рассмотрим ситуацию, когда изображение занимает на картинной плоскости прямоугольную область 

Однородные координаты. Задание геометрических преобразований в однородных координатах с помощью матриц
В предыдущей главе описывались геометрические преобразования на плоскости и в пространстве, а также было показано, как можно использовать аппарат матриц для таких задач. Для преобразований на плоскости применялись двумерные векторы и матрицы размерностью 

Для пояснения такого подхода сначала рассмотрим случай двумерного пространства. Каждая точка плоскости с координатами 
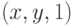

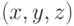


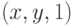
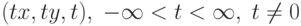
Если теперь рассматривать точку плоскости как принадлежащую трехмерному пространству, то ее двумерные преобразования можно будет описывать с помощью матриц 
Поворот на угол 
Перейдем теперь к трехмерному пространству. Каждой точке 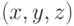



Матрица поворота относительно оси 

Путем объединения приведенных элементарных преобразований можно построить и более сложные. В третьей главе мы использовали произведение простых матриц вращения для построения матрицы поворота относительно произвольной оси. Приведем один пример.
Пусть в пространстве заданы два отрезка — 

- Сдвиг, перемещающий точку
в точку
.
- Сдвиг начала координат в эту же точку.
- Если отрезки неколлинеарны:
- строится вектор нормали к плоскости, в которой лежат отрезки (для этого можно использовать векторное произведение исходных векторов);
- поворот относительно вектора нормали, совмещающий два отрезка по направлению (угол поворота можно определить с помощью скалярного произведения исходных векторов).
Каждое из этих преобразований реализуется с помощью матрицы, а полное преобразование можно выполнить, используя произведение матриц.
Использование матриц очень удобно для выполнения преобразований в пространстве, хотя в некоторых случаях это приводит к избыточному числу выполняемых операций. Например, поворот одной точки в пространстве относительно координатной оси 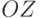
Источник









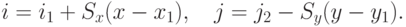





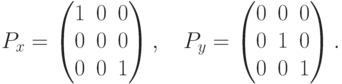





 в точку
в точку  .
.


