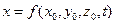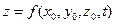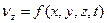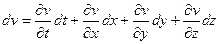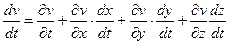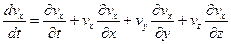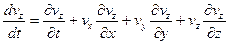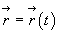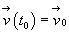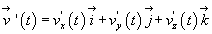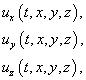Способы описания движения жидкости

Методы описания движения жидкости

Кинематика жидкости — раздел механики жидкости, в котором изучаются движение жидкости и его характеристики, но не рассматриваются силы, под действием которых осуществляется это движение.

В кинематике устанавливаются закономерности между координатами жидких частиц, их скоростями, ускорениями и другими параметрами, и изменениями этих параметров во времени.

Механическое состояние движущейся жидкости в любой точке внутри ее характеризуется двумя величинами: скоростью движения частиц жидкости и гидродинамическим давлением.

Представление о жидкости как о сплошной среде позволяет считать эти параметры непрерывными и дифференцируемыми функциями координат и времени. Существуют два способа описания движения жидкости:

1.Способ Лагранжа, который заключается в задании текущих значений координат каждой рассматриваемой материальной точки как функции времени. Способ Лагранжа теоретически применим к описанию движения жидкости, если рассматривать это движение, как непрерывный поток частиц жидкости, составляющих сплошную среду. Движение жидкости определено, если для каждой частицы жидкости можно указать координаты , как функции начального положения и времени . Кинематические уравнения движения записываются при этом в виде функциональной зависимости:

(4.1)

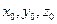
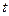
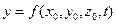
Переменные 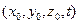называют переменными Лагранжа

Несмотря на полную информацию о движении массы жидкости, которую дает метод Лагранжа, он не получил широкого применения в механике жидкости. Это связано с тем, что уравнения движения, составляемые на основе метода Лагранжа сложны и трудноразрешимы. По этой причине наиболее широкое применение в механике жидкостей находит метод Эйлера.

2. Способ Эйлера основан на том, что совокупность мгновенных местных скоростей во всей области пространства, занятого движущейся жидкостью представляет собой векторное поле, называемое полем скоростей. В поле скоростей выбирают фиксированную точку, в которой отслеживают изменения скоростей с течением времени. Переменные 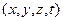называют переменными Эйлера

Векторное поле скоростей может быть выражено и через проекции скоростей на соответствующие координатные оси в виде:

(4.2)

Так как состояние движущейся жидкости в каждой точке пространства определяется мгновенной локальной скоростью и значением гидродинамического давления, то описание движения жидкости сводится к определению поля скоростей и поля давлений во всем объеме, занимаемом движущейся жидкостью.

Полный дифференциал скорости будет равен:

Разделим данное уравнение на

Запишем уравнение на три координатные плоскости:

(4.3)

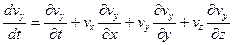
где левые части – полные производные ускорения в данных точках;

первые слагаемые правых частей – частные производные по времени -представляют собой проекции локального ( местного) ускорения в точке;

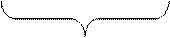
выделенные фигурной скобкой – конвективные производные;

выделенные по диагонали – прямые конвективные производные.

Важнейшей кинематической характеристикой, необходимой для составления динамических уравнений движения жидкости является ускорение.

В соответствии с физическим смыслом ускорение материальной точки или отдельной частицы жидкости определеяется полной производной вектора скорости по времени:

Местная производная указывает на стационарность (нестационарность) процесса. Или на установившееся и неустановившееся движения жидкости.

Установившимся (стационарным) называют движение, при котором основные параметры потока (скорость, давление, плотность) в данной точке пространства не изменяются с течением времени. Например, если скорость остается постоянной во времени, то 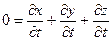или .

Конвективная производная показывает однородность (равномерность) поля скоростей.

Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае 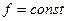; средние скорости по длине потока также не изменяются, т.е. . Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.

Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и постоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.

Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).

Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.

Если уровень жидкости в резервуаре поддерживать все время постоянным , путем непрерывного подвода жидкости в сосуд из крана, то форма струи, дальность ее полета и расход жидкости через отверстие будут постоянными. Этот случай является иллюстрацией установившегося движения жидкости.

Примером неустановившегося движения является истечение жидкости из отверстия в резервуаре. По мере понижения уровня жидкости в сосуде с течением времени (моменты времени 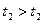) уменьшается дальность полета струи и расход вытекающей жидкости.

Дата добавления: 2015-04-21 ; просмотров: 720 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Способы описания движения жидкости

Рассмотрим некоторый ограниченный сосуд Ώ с границей Г целиком заполненный жидкостью.

Ω

Пусть, начиная с некоторого момента времени t₀, на жидкость начинает действовать некоторые силы. Это могут быть, например, механические силы (силы перемешивания, силы тяжести, центробежная силы и т.д.).

Тогда жидкость, вообще говоря, придет в движение. Если, к тому же, она в момент времени t₀ находилась в движении, то характер движения в последующие моменты времени t будет зависеть от характера движения в начальный момент времени.

Нашей задачей является описание движения жидкости в моменты времени 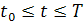, в зависимости от начального состояния жидкости и действующих на жидкость сил.

Исторически сложились два принципиально различных подхода к описанию движения жидкости.

1. Подход Лагранжа

Жидкость представляется, как совокупность материальных частиц, заполняющих сосуд (объем) Ώ, причем эти частицы считаются настолько малыми, что их можно отождествить с точками объема Ώ.

Т.о. объектом исследования в этом подходе является частица жидкости.

Сущность подхода Лагранжа заключается в распространении на жидкость обычных приемов механики системы материальных точек.

Т.о. траектория движения частицы жидкости описывается уравнениями

(4.1)

— параметры, которые дают возможность отличить одну частицу от другой.

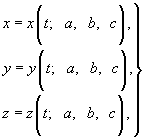
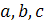
Для определенности понимают в качестве 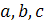— координаты данной частицы в некоторый фиксированный (единый для всех частиц) момент времени.

Скорости движения частицы определяются выражениями:

(4.2)

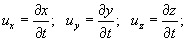
2. Подход (способ) Эйлера

В современной гидродинамике используется в основном способ Эйлера благодаря простоте, а также удобству применения хорошо разработанного математического аппарата теории поля.

Объектом исследования в подходе Эйлера является поле – часть пространства, занимаемого движущейся жидкостью.

Для жидкости применяется модель сплошной среды (т.е. используется гипотеза сплошности).

При использовании подхода Эйлера нет надобности изучать движение каждой фиксированной частицы жидкости – достаточно знать кинематические характеристики в каждой неподвижной точке пространства и исследовать как меняются эти характеристики при переходе из одной точки к другой.

Т.о. при подходе Эйлера движение считается заданным, если определено поле вектора скорости

(4.3)

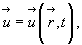
где 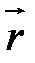— радиус вектор точки пространства.

Выражение (4.3) эквивалентно трем скалярным равенствам:

(4.4)

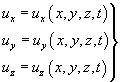
Однако в некоторых случаях возникает необходимость определения траекторий частиц жидкости (подхода Лагранжа).

В этом случае задача исследования формулируется следующим образом:

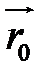
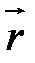
Если в начальный момент t₀ частица жидкости занимала положение , а ее движение описывается с помощью функции (t), то

Каждой частице объема Ώ соответствует своя вектор-функция 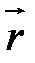(t), описывающая ее движение.

Движение жидкости будет описано, если будут найдены все эти вектор-функции 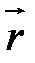(t).

Для этого зафиксируем момент времени t. В этот момент времени частица жидкости, двигающаяся по закону 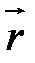(t) имеет скорость

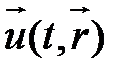
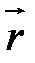
Обозначим через скорость частицы жидкости в момент времени t в точке . Ясно, что должно выполняться соотношение

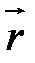
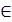
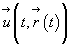
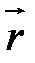
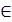
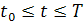
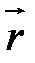
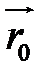
Отсюда следует, что если известны скорость движущейся жидкости в каждой точке Ώ в каждый момент времени t, т.е. известна вектор-функция , определенная для всех Ώ и всех , то для того, чтобы найти вектор-функцию (t), описывающую движение частицы жидкости, занимающей в начальное время t₀, положение , надо решить следующую задачу Коши для векторного дифференциального уравнения:

(4.5)

Если расписать 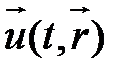в координатах, т.е. представить ее в виде

то задачу (4.5) можно переписать в виде задачи Коши для системы обыкновенных дифференциальных уравнений

(4.6)

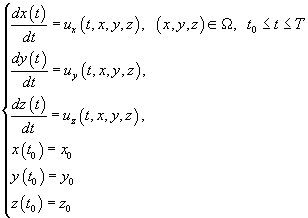
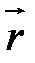
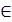
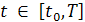
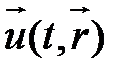
Т.о., для того, чтобы описать движение жидкости, достаточно знать распределение скоростей жидкости в каждой точке Ώ и в каждый момент времени , или, что то же, знать вектор-функцию .

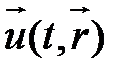
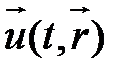
Оказывается, для того, чтобы найти , нужно в свою очередь решить некоторую систему уравнений, которой удовлетворяет .

Т.о. задачу, которую мы должны решить, можем сформулировать следующим образом:

Пусть в области Ώ трехмерного координатного пространства 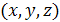с гладкой границей Г происходит движение жидкости.

Требуется вывести систему уравнений, которой удовлетворяют функции

являющиеся координатами вектор-функции 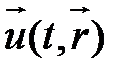— поля скоростей движущейся жидкости.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Источник