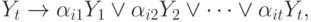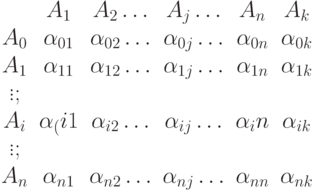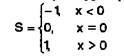Алгоритмы на графах — Часть 0: Базовые понятия
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень равна исходящей).
Входящая степень вершины v это количество ребер вида (i, v), то есть количество ребер которые «входят» в v.
Исходящая степень вершины v это количество ребер вида (v , i), то есть количество ребер которые «выходят» из v.
Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Представление графов
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| 2 ).
В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Применение
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Заключение
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
В следующей части
BFS — Алгоритм поиска в ширину
Библиография
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»
Источник
Способы описания работы дискретных устройств
3.2 Граф-схемы алгоритмов
ГСА находят широкое применение в практике проектирования устройств ЦВМ и, в частности, микропрограммных автоматов в силу их хорошей обозримости, простоты конструкции языка и возможности преобразований и формального перехода к автоматному отображению.
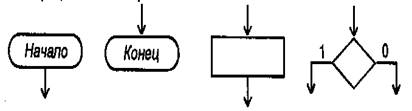
Основными символами, используемыми при записи граф -схем алгоритмов (ГСА), будем считать:
- операторы,
- логические условия,
- стрелки (рис.3.6).
Из всего множества операторов выделяются:
- начальный оператор
, - конечный оператор ,
- произвольный оператор .
.Начальный оператор в дальнейшем (если это особо не оговаривается) будем рассматривать как оператор, символизирующий начало работы алгоритма.
Особенность записи оператора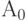 
в ГСА состоит в том, что в этот оператор не входит ни одной стрелки.
Конечный оператор будем рассматривать как оператор, символизирующий конец работы алгоритма.
Особенность записи оператора и 
в ГСА состоит в том, что из этого оператора не выходит ни одной стрелки.
Произвольные операторы будем рассматривать как символы, обозначающие определённые действия, акты, связанные с реализацией алгоритма.
Особенность записи операторов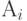 
состоит в том, что в эти операторы могут входить несколько стрелок, но выходит всегда только одна стрелка.
Под логическим условием будем понимать логическую функцию вида 
, где 
элементарные логические условия. Особенность записи логических условий состоит в том, что они могут иметь несколько входящих стрелок и только две выходящие, помеченные символами «О» и «I» в со-ответствии со значением логического условия. В дальнейшем будем допускать также ГСА замену левой части выражения вида 
его правой частью.
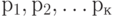
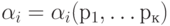
Стрелки обеспечивают упорядочение последовательности выполнения операторов и проверки логических условий, а также их взаимосвязей.
Выполнение алгоритма всегда начинается с оператора 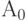и заканчивается оператором .
3.3Формулы переходов
В общем виде для каждой операторной вершины формула перехода записывается так:
причем свойства ортогональности и полноты так же соблюдаются. Кроме того считается, что значения наборов логических условий в процессе выполнения операторов не меняются.
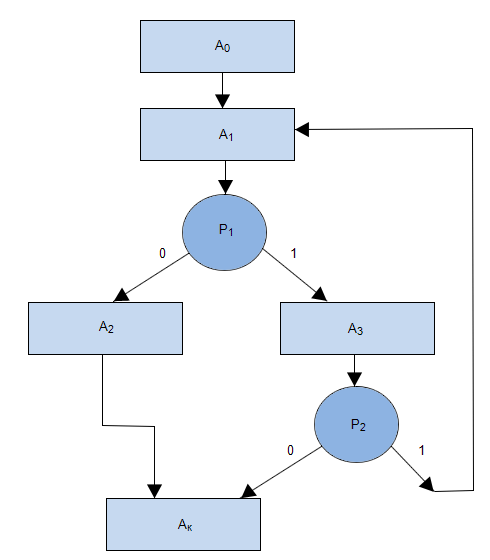
Для МП, представленной на рис.3.7, формулы перехода будут записаны так:
;
;
;
;
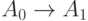
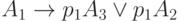
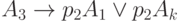
3.4. Матричные схемы алгоритмов
Говорят, что задана матричная схема алгоритма (МСА), если задана матрица вида
где 
— операторы ,
— начальный и конечный операторы ,
— логические условия, имеющие тот же смысл, что и в ГСА.
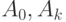
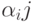
| А1 | А2 | А3 | Аk |
|---|---|---|---|
| A0 | 1 | ||
| A1 | p1 | p1 | |
| A2 | 1 | ||
| A3 | p2 | p2 |
В MCA 
принято рассматривать как такую логическую функцию , что если выполнялся оператор 
и на образовавшемся наборе 
значений элементарных логических условий функция 
получила значение , равное единице, то непосредственно после оператора должен выполняться оператор 
.
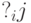
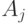
В рис.3.1,а приводится МСА МП, показанной на рис.3.7.
Источник
Граф-схемы алгоритмов
4. Граф-схемы алгоритмов
ГСА – это ориентированный связный граф, задающий последовательность выполнения операций данного алгоритма и содержащий ряд операторных и условных вершин, а также одну начальную и одну конечную вершины. Операторной называется вершина, – которой сопоставляется одна или несколько микроопераций и отмечается соответствующими управляющими сигналами У, а условной – вершина, которой сопоставляется некоторое логическое условие X.
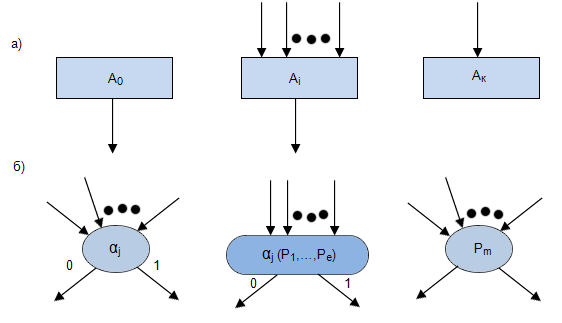
Любая вершина ГСА, кроме вершины «Начало», имеет по одному входу. Вершина «Начало» входов не имеет. Вершина «Начало» и любая операторная вершина имеют по одному выходу. Вершина «Конец» выходов не имеет. Любая условная вершина имеет два выхода, помечаемых символами «Да» и «Нет»: Вместо этих символов могут быть использованы цифры «1» и «О» соответственно. Изображение вершин «Начало», «Конец», операторной вершины и условной вершины ГСА представлено на рис. 2.
Рисунок 2-Графы схемы алгоритмов
ГСА составляют так, чтобы обеспечить выполнение необходимых операций и проверку логических условий в соответствии со словесным описанием алгоритма.
На основании перечня микроопераций и реализующих их функциональных узлов составляется структурная схема ОА. Здесь широкими стрелками показаны шины, по которым передается информация, а тонкими – сигналы у, управляющие работой отдельных узлов или передачей информации по шинам.
ГСА должна удовлетворять следующим условиям:
1. Входы и выходы вершин соединяются друг с другом с помощью направленных всегда от выхода к входу.
2. Каждый выход соединен только с одним входом.
3. Любой вход соединяется, по крайней мере, с одним выходом.
4. Любая вершина ГСА лежит, по крайней мере, на одном пути из вершины «Начало» в вершину «Конец».
5. Один из выходов условной вершины может соединяться с ее входом, что недопустимо для операторной вершины. Такие условные вершины иногда называются возвратными.
6. В каждой условной вершине записывается логическое условие из множества логических условий. Разрешается в различных условных вершинах записывать одинаковые логические условия.
7. В каждой операторной вершине записывается оператор, представляющий собой выходной сигнал или совокупность выходных сигналов управляющего автомата. Разрешается в различных операторных вершинах записывать одинаковые операторы.
5. Содержательные граф-схемы алгоритмов
Обычно при проектировании различных устройств предварительно составляется так называемая содержательная ГСА, в которой внутри условных и операторных вершин записаны логические условия и микрооперации в содержательных терминах.
В качестве примера построим содержательную ГСА устройства, вычисляющего функцию знака числа:
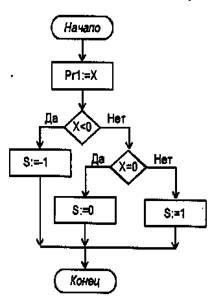
Соответствующая содержательная ГСА представлена на рис. 3.
Рисунок 3. Содержательная ГСА функции определения знака числа
6. Синтез управляющего автомата по граф-схеме алгоритма
Конечный управляющий автомат, реализующий микропрограмму работы дискретного устройства, принято называть микропрограммным автоматом. Как уже отмечалось, микропрограмма отображается с помощью ГСА. Рассмотрим последовательность этапов синтеза управляющего автомата по его ГСА.
1. Запись словесного алгоритма функционирования операционного автомата (выполняемых операций) с учетом структуры операционного автомата.
2. Построение содержательной ГСА функционирования операционного автомата.
3. Построение отмеченной ГСА с учетом типа автомата.
4. Построение графа переходов автомата или таблицы переходов.
5. Проведение структурного синтеза автомата по его графу переходов известными методами, например, с помощью канонического метода структурного синтеза.
Построение отмеченной ГСА производится по содержательной ГСА. Для автоматов Мили и Мура процедура разметки имеет различия.
6.1 Построение отмеченной ГСА автомата Мили
Если необходимо построить микропрограммный автомат Мили, то содержательная ГСА управляющего автомата размечается в соответствии со следующими правилами:
1) символом состояния a1 отметить вход вершины, следующей за вершиной «Начало», а также вход вершины «Конец»;
2) входы всех вершин, следующих за операторными, должны быть отмечены символами а с последовательными индексами;
3) если выход вершины отмечается, то только одним символом;
4) входы различных вершин, за исключением вершины «Конец», отмечаются различными символами;
5) содержательные термины микроопераций и логических условий. заменяются их условными обозначениями: в каждой операторной вершине последовательно проставляются символы выходных сигналов, если в различных операторных вершинах записаны одинаковые микрооперации, то разрешается их отмечать одинаковыми символами выходных сигналов; если в различных условных вершинах записаны одинаковые логические условия, то разрешается их отмечать одинаковыми символами входных сигналов.
6.2 Построение отмеченной ГСА автомата Мура
Если необходимо построить микропрограммный автомат Мура, то содержательная ГСА управляющего автомата размечается в соответствии со следующими правилами:
1) символом a1 отмечаются вершины «Начало» и «Конец»;
2) различные операторные вершины отмечаются различными символами;
3) все операторные вершины должны быть отмечены.
4) содержательные термины микроопераций и логических условий. заменяются их условными обозначениями.
Содержательная ГСА (рис. 3.) после разметки по приведенному алгоритму представлена на рис. 5.
После получения отмеченной ГСА строится граф переходов автомата. Он имеет столько различных вершин, сколько различных букв аi с индексами имеется в отмеченной ГСА. Каждая вершина графа переходов автомата отмечается буквой а с соответствующим индексом.
Между двумя вершинами графа имеется дуга, если на отмеченной ГСА между вершинами с метками ai и ak, имеется путь. Над дугой ставится входной сигнал, равный конъюнкции логических условий соответствующего пути в отмеченной ГСА. При этом выполнению логического условия соответствует переменная без отрицания, а невыполнению логического условия – переменная с отрицанием на соответствующей дуге графа переходов автомата.
Если в отмеченной ГСА между упомянутыми вершинами с метками ai и аk имеется несколько путей, то в графе переходов автомата на дуге, связывающей аi и аk через символ дизъюнкции перечисляются все конъюнкции, соответствующие имеющимся путям.
Если строится граф переходов автомата Мура, то символы микроопераций (выходные сигналы управляющего автомата) записываются около соответствующих его вершин. Для автомата Мили символы микроопераций записываются на соответствующих дугах при конъюнкциях логических условий, описывающих путь через операторную вершину с рассматриваемой микрооперацией.
Если в отмеченной ГСА имеется безусловный переход между операторными вершинами, т.е. путь, не проходящий ни через какие условные вершины, то на графе переходов автомата ему соответствует дуга, которой приписывается входной сигнал «1», показывающий, что данный переход в автомате осуществляется при поступлении очередного синхросигнала.
В дальнейшем синтез проводится с помощью описанного ранее метода структурного синтеза. Подчеркнем, что входными сигналами синтезируемого структурного автомата являются конъюнкции булевых переменных (или дизъюнкции конъюнкций), каждая из которых отображает путь через соответствующие условные вершины отмеченной ГСА, а выходными сигналами – микрооперации, обозначающие либо вершины, либо дуги графа переходов автомата, в зависимости от его типа. Используя канонический метод структурного синтеза, можно построить функциональную схему автомата.
Источник
