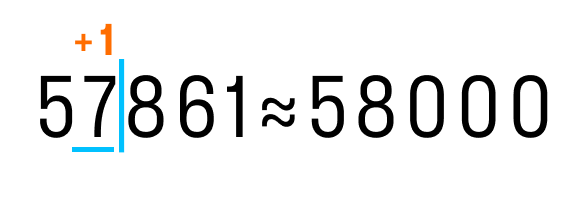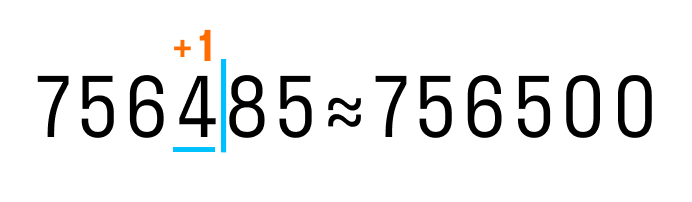Способы округления положительных десятичных дробей

Приближенные значения чисел. Округление чисел

Округление натуральных чисел

Когда полная точность не нужна или невозможна, числа округляют, т.е. заменяют близкими числами с нулями на конце. Например, на концерт продано 9 678 билетов, данное число в разговоре можно заменить выражением «около 10 тыс. билетов». В таком случае число 10 тыс. называют приближенным значением числа 9 678 и говорят, что число 9 678 округлили до числа 10 тыс. Записывают 9 67810 тыс.

В зависимости от ситуации натуральные числа округляют до того или иного разряда: до десятков, до сотен, до тысяч и т.д.

Правило округления натуральных чисел

К цифре разряда, до которого округляют число, прибавляют 1, если справа от нее стоят цифры 5, 6, 7, 8 или 9, а если справа от нее стоят цифры 0, 1, 2, 3 или 4, то цифру округляемого разряда оставляют без изменения; все цифры, расположенные правее разряда, до которого округляют число, заменяют нулями.

Примеры:

а) Округлим до сотен тысяч число 1 456 345.

Подчеркиваем цифру в разряде сотен тысяч 1 4 5 6 345. Справа от подчеркнутой цифры стоит 5, поэтому прибавляем к цифре подчеркнутого разряда 1 и заменяем нулями все цифры, расположенные справа от подчеркнутой, получим 1 500 000.

Записывают решение так: 1 456 3451 500 0001 млн 500 тыс.

б) Округлим до миллионов число 32 123 574.

Подчеркиваем цифру в разряде миллионов 32 1 2 3 574. Справа от подчеркнутой цифры стоит 1, поэтому цифру подчеркнутого разряда оставляем ту же и заменяем нулями все цифры, расположенные справа от подчеркнутой, получим 32 000 000.

Записывают решение так: 32 123 57432 000 00032 млн.

Обратите внимание: в круглом числе должно получится столько же цифр, как и в исходном.

Если мы число округляем в большую сторону (т.е. прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с избытком, если же округляем число в меньшую сторону (т.е. не прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с недостатком.

Округление десятичных дробей

В зависимости от ситуации десятичные дроби можно округлять до следующих разрядов: единиц, десятых, сотых, тысячных и т.д.

Правило округления десятичных дробей

К цифре разряда, до которого округляют число прибавляют 1, если справа от нее стоят цифры 5, 6, 7, 8 или 9, а если справа от нее стоят цифры 0, 1, 2, 3 или 4, то цифру округляемого разряда оставляют без изменения; все цифры, расположенные правее разряда, до которого округляют число, отбрасывают.

Пример:

а) Округлим дробь 0,789036 до десятых.

Округление осуществляем до десятых, поэтому после запятой мы должны оставить одну цифру. Подчеркиваем цифру разряда десятых 0,7 8 9036. Справа от разряда десятых стоит цифра 8, поэтому прибавляем 1 к цифре разряда десятых и все цифры, расположенные правее разряда десятых отбрасываем, получим 0,8.

Записывают решение так: 0,7890360,8.

б) Округлим дробь 0,29604 до сотых.

Округление осуществляем до сотых, поэтому после запятой мы должны оставить две цифры. Подчеркиваем цифру разряда сотых 0,29 6 04. Справа от разряда сотых стоит цифра 6, поэтому прибавляем 1 к цифре разряда сотых и все цифры, расположенные правее разряда сотых отбрасываем, получим 0, 30.

Записывают решение так: 0,296040,30.

Обратите внимание: прибавив единицу к цифре 9 в разряде сотых получим 10 сотых. Поэтому в разряде сотых оказался 0, а в разряде десятых добавилась одна разрядная единица.

Также как и при округлении натуральных чисел, если мы число округляем в большую сторону (т.е. прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с избытком, если же округляем число в меньшую сторону (т.е. не прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с недостатком.

Поделись с друзьями в социальных сетях:

Источник

Округление десятичных дробей

На предыдущей странице мы обсудили, как округлить натуральное число. Теперь рассмотрим, как округлить десятичную дробь.

Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д.

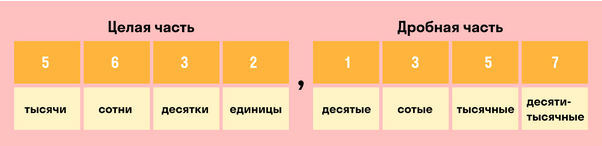
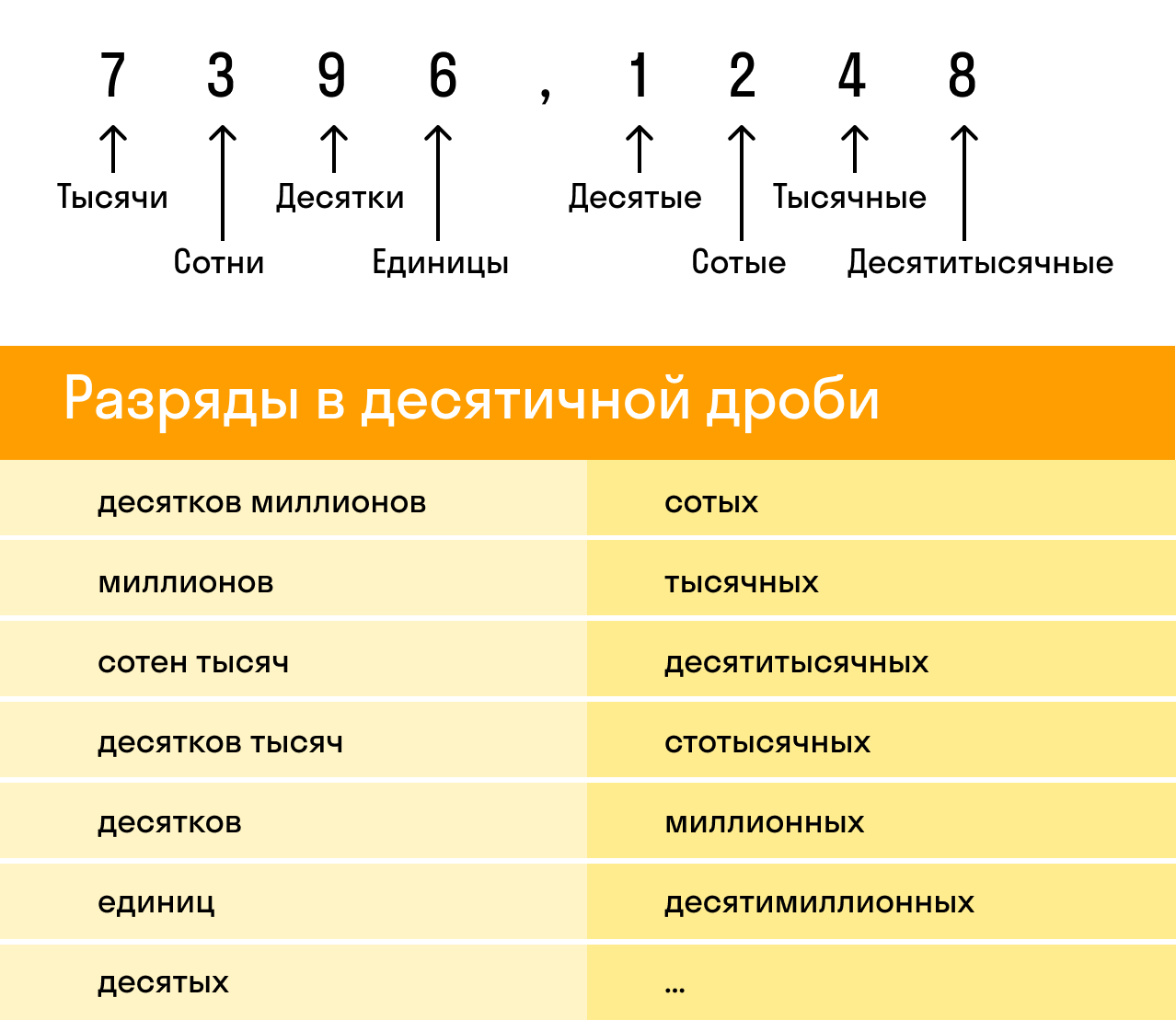
Важно помнить и не путать названия разрядов до и после запятой в десятичной дроби.

Правила округления десятичной дроби

При округлении дробной части десятичной дроби пользуемся правилами округления.

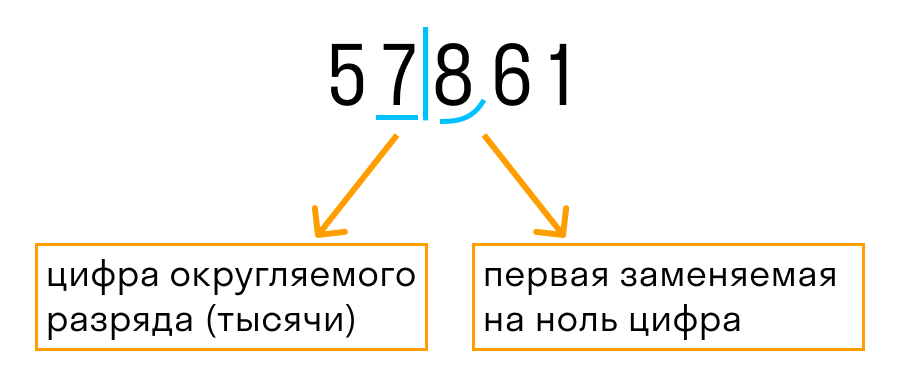
1. Подчёркиваем цифру округляемого разряда.
2. Вертикальной чертой отделяем все цифры, стоящие справа от округляемого разряда.
3. Если справа от подчёркнутой цифры стоит цифра 0, 1, 2, 3 или 4 , то подчёркнутую цифру оставляем без изменений, а все цифры после вертикальной черты отбрасываем.
4. Если справа от подчёркнутой цифры стоит цифра 5, 6, 7, 8 или 9 , то к подчёркнутой цифре добавляем 1 , а все цифры после вертикальной черты отбрасываем.

Округлим 41,958 до сотых.

Округлим 0,748 до десятых.

Округлим десятичную дробь 14,89 до разряда единиц в целой части.

Если при округлении десятичной дроби последняя из оставшихся цифрой в дробной части оказывается 0 , то отбрасывать этот ноль нельзя.

Так как в таком случае данный ноль в дробной части показывает, до какого разряда округлено число.

Пример. Округление 5,038 до десятых.

Еще один пример:

Обратите внимание, что в примере, в разряде сотых стоит цифра 9 , которая при добавлении 1 , превращается в 10 . Поэтому вместо 9 записываем ноль, а к разряду десятых (у нас это 8 ) прибавляем 1 .

Если десятичную дробь нужно округлить до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.

Источник

Округление десятичных дробей

О чем эта статья:

Правила округления десятичной дроби

Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.

В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:

Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).

Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.

Число, полученное при округлении, называют приближенным значением данного числа.

Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.

Если число c

Еще одно правило округления, которое нужно запомнить

Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число.

Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.

Примеры округления десятичной дроби

Давайте разберем несколько примеров округления дробной части десятичных дробей.

Пример 1. Округлите дробь 56,786 до сотых.

Цифра, которую нужно округлить, — 8. Обращайтесь к таблице с подсказками названия разрядов, чтобы верно определять нужную цифру.

Справа от цифры округляемого разряда цифра 6.

Смотрим на пункт 4. Прибавляем: 8 + 1 = 9.

Ответ. 56,786 ≈ 56,79.

Пример 2. Округлите дробь 0,647 до десятых.

Округляемая цифра — 6.

Смотрим пункт 3. Значит, цифра 6 остается неизменной.

Пример 3. Округлите дробь 23,98 до разряда единиц в целой части.

Цифра, которую нужно округлить, — 3.

Первая цифра после запятой — 9. Значит, нужно прибавить: 3 + 1.

Затем отбрасываем все остальные цифры, стоящие справа.

Пример 4. Округлите дробь 3,286 до десятых.

Цифра, которую нужно округлить, — 2.

Согласно правилу, прибавляем: 2 + 1.

Затем отбрасываем все остальные цифры, стоящие справа.

Пример 5. Округлите дробь 45,387 до сотых.

Прибавляем: 8 + 1.

Затем отбрасываем все остальные цифры, стоящие справа.

Источник

Правильное округление чисел

О чем эта статья:

Приближенные значения

В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.

У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин, иногда можно использовать приближенные значения.

Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.

Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.

Если длина платья 1м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.

Приближенное значение — число, которое получилось после округления.

Для записи результата округления используют знак «приблизительно равно» — ≈.

Округлить можно любое число — для всех чисел работают одни и те же правила.

Округлить число значит сократить его значение до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.

Округление натуральных чисел

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.

Особенности натуральных чисел:

• Наименьшее натуральное число: единица (1).
• Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
• У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Правила округления чисел:

1. Подчеркнуть цифру разряда, до которого надо округлить число.
2. Отделить все цифры справа от этого разряда вертикальной чертой.
3. Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
4. Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.

Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.

Теперь округлим 756 485 до сотен:

Округлим число 123 до десятков: 123 ≈ 120.

Округлим число 3581 до сотен: 3581 ≈ 3580.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.

• как округлить число 697 до десятков — 697 ≈ 700;
• как округлить число 980 до сотен — 980 ≈ 1000.

Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:

• 7 882 000 = 7 882 тыс.
• 1 000 000 = 1 млн.

Округление десятичных дробей

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных.

Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.

Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.

То натуральное число, к которому дробь ближе, называют округленным значением числа.

Цифра, которая записана в данном разряде:

• не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
• увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.

Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.

Как округлить до десятых. Оставить одну цифру после запятой. Изи!

Как округлить до сотых. Оставить две цифры после запятой.

Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.

Пример 1.

256,43 ≈ 256,4 — округление до десятых;

4,578 ≈ 4,58 — округление до сотых;

17,935 ≈ 18 — округление до целых.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.

Пример 2.

79,7 ≈ 80 — округление до десятков;

0,099 ≈ 0,10 — округление до сотых.

Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса. А после можно пользоваться онлайн калькулятором, чтобы выиграть время и решать быстрее всех.

Статья «Больше, меньше или равно» может оказаться для тебя полезной!

Источник