Способы обработки результатов наблюдения

Методы обработки результатов наблюдений

Одним из основных способов изучения окружающего нас мира, средством познания было и остается наблюдение. Под наблюдением принято принимать целенаправленное восприятие свойств процессов и явлений. Опираясь на результаты наблюдения, человек строит физическую модель новых процессов и явлений, выдвигает научные гипотезы, делает открытия, создает теорию, принимает решения. Наблюдения сопровождается приемом, определенным преобразованием и регистрацией человеком информации о свойствах наблюдаемого объекта. Регистрация результатов наблюдения может производится как в памяти ( мозге) человека- наблюдателя, так и на специальных носителях информации ( бумаге, магнитной ленте, полотне художника, фотопленке и т.д.). Характер наблюдения существенным образом зависит от профессиональной направленности наблюдателя.

В то же время от наблюдения до принятия решения получаемая человеком информация претерпевает, как правило, существенные преобразования. Наиболее характерными этапами таких преобразований в большинстве сфер человеческой деятельности являются измерения и обработка результатов измерений.

Измерение состоит в сравнении наблюдаемой величины (свойства объекта) с эталоном и получении в результате этого ее численного значения. Если результаты наблюдений представлены в виде цифр и графиков, то имело место измерение. Иногда, кроме измерения, различают подсчет. Подсчет можно квалифицировать как завершающий этап наблюдения – регистрацию величин дискретного типа (число деталей, обрабатываемых за смену, и т.п.).

Допустим, что в результате n измерений случайной величины Х получена последовательность значений х₁,х₂,…, х_n, которая называется простым статистическим рядом или выборкой. Обычно выборка оформляется в виде таблицы, в первой колонке которой стоит номер опыта i, а во второй значение случайной величины.

Первичная обработка выборки состоит в группировке найденных значений по достаточно малым интервалам, вычислении средних относительных частот для каждого интервала и графическом представлении результатов в виде гистограммы или эмпирической функции распределения. Число интервалов k можно определить по формуле:

Полученное значение округляют до ближайшего целого числа. Число интервалов не должно превышать 10-20. Ширина интервалов ∆х выбирается одинаковой и равной:

Все значения случайной величины, попавшие в некоторый интервал, относятся к его середине.

Пример 1:Ежесуточный выпуск кузнечным цехом поковок m(т/сут) регистрировался в течении n=36 сут. Необходимо построить статический ряд, гистограмму и эмпирическую функцию распределения случайной величины m. Данные в таблице:

I
M	1,8	32,7	3,6	1,9	25,1	25,4	5,3	6,6	24,7
I
M	6,9	7,7	25,2	8,8	23,0	9,7	11,3	20,7	21,2
I
M	21,8	12,7	21,5	13,3	21,8	13,0	14,5	15,8	14,1
I
M	15,2	17,2	16,3	17,9	13,5	16,6	15,1	17,0	15,0

Решение:k= 1+3,2 lgn= 1=3,2∙lg36≈7 – число интервалов, на которые разбивается диапазон наблюдений.

Находим ширину интервала от 0 до 35 т/сут.

Результаты наблюдений можно свести в представленный ниже статистический ряд:

Параметр	Значения параметра по номеру интервала
Интервал ∆m,т/сут	0…5	5…10	10…15	15…20	20…25	25…30	30…35
Среднее 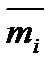,т/сут	2,5	7,5	12,5	17,5	22,5	27,5	32,5
Число наблюдений ni	7,5	8,5
Частота ni/n	0,0833	0,1666	0,2084	0,2362	0,1944	0,0833	0,0278

Построение гистограммы: по оси абсцисс откладываем интервалы, и на каждом из них, как на основании, строится прямоугольник, площадь которого равна частоте данного интервала (с тем, чтобы площадь всей гистограммы была равна 1). В нашем случае все интервалы имеют одинаковую ширину и поэтому высоты прямоугольников равны соответствующим частотам (рис. 1).

Рис.1. Гистограмма ежесуточного выпуска поковок

Для построения эмпирической функции распределения достаточно несколько точек, в качестве которых удобно взять границы интервалов:

График эмпирической функции распределения приведен на рис.2.

Рис. 2. Эмпирическая функция распределения ежесуточного выпуска поковок; штриховой линией показана кривая для нормального закона распределения

Важнейшими характеристиками эмпирического распределения являются среднее арифметическое значение (выборочное среднее) и среднее квадратичное отклонение (выборочная дисперсия)

; s 2 .

При увеличении числа наблюдений n среднее арифметическое значение будет приближаться к математическому ожиданию, а среднее квадратичное отклонение – к дисперсии, т.е. при n→∞ справедливы соотношения: →M и s 2 →D .

Пример 2. Найти математическое ожидание, дисперсию и среднеквадратичное отклонение случайной величины, рассмотренной в примере 1.

M 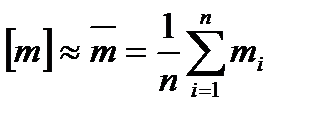=1/36(1,8+32,7+…+15,0) = 15,4 т/сут;

D = 1/35(1/8-15,4) 2 +(32,7-15,4) 2 +…+(15,0-15,4) 2 = 53,2(т/сут) 2 ;

σ ≈ s = т/сут.

Пример 3 .Записать в виде вариационного и статистического рядов

выборку 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4.

Решение. Объем выборки n = 15. Упорядочив элементы выборки по

величине, получим вариационный ряд

2, 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7, 10, 10 .

Статистический ряд записывается в виде таблицы

xi

ni

Пример 4.Определить выборочные среднее, дисперсию, моду и ме-

диану для выборки: 5, 6, 8, 2, 3, 1, 4, 1 .

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4,

5, 6, 8. Выборочное среднее находим по формуле (13.1).

= 1/8 (1+1+2+3+4+5+6+8) = 3,75.

Для расчета выборочной дисперсии воспользуемся формулой (13.3).

D

=8/7 ( 1/8 (1+1+4+9+16+25+36+64) — 3,752 ) = 6,21 .

Все элементы входят в выборку по одному разу, кроме 1, следовательно,

выборочная мода d X

= 1. Так как n = 8, то медиана hX

Ответ: ; s 2 =6,21; dx=1; hx=3,5.

Источник

Программа наблюдения и обработка результатов

Вся изложенная выше информация о наблюдении оказывается необ­ходимой при разработке программы наблюдения, в соответствии с которой осуществляется конкретная процедура наблюдения.

Программа наблюдения составляется с учетом требований, которые необходимо выполнить для проведения наблюдения и при обработке его результатов, а именно:

а) сформулировать и записать цель наблюдения и предмет наблю­дения (исследования);

б) определить объекты, которое будут фиксироваться при наблю­дении, и все их выписать, убедившись, что через них есть возможность познать наблюдаемый психологический феномен;

в) определить и описать ситуации, в которых будет проводиться наблюдение;

г) установить временные рамки наблюдения и составить его гра­фик;

д) определить форму регистрации наблюдаемых объектов (или вид записи) и оценить возможность сопоставления наблюдаемых фактов, полученных в разное время или в разных ситуациях, возможно, разны­ми наблюдателями;

е) разработать или заготовить (если уже есть готовые формы) блан­ки регистрации наблюдаемого явления, если имеется такая необходи­мость.

Составленная в соответствии с этими требованиями программа важна, прежде всего, самому наблюдателю, поскольку в ней в письмен­ном виде регистрируется все то, что составляет основу конкретной ме­тодики наблюдения.

В истории метода наблюдения уже сложились некоторые представ­ления об условиях объективности полученных данных, одно из них — проведение многократных длительных наблюдений. Для выполнения этого требования наличие программы оказывается просто необходи­мым, так как программа организует наблюдение иногда на протяже­нии длительного периода, обеспечивая сохранение единообразия про­цедуры.

Другой способ повышения достоверности данных, получаемых в I наблюдении, — проведение независимого наблюдения несколькими наблюдателями. В этом случае также необходима программа как руко­водство к наблюдению для разных людей. Во второй главе вы найдете программы наблюдения различных психических явлений, которые со­ставили основу конкретных методик наблюдения.

Несколько замечаний по поводу процедуры наблюдения. Вы уже обратили внимание на то, что ей предшествует и теоретическая, и твор­ческая работа наблюдателя по созданию методики наблюдения. И все-таки перед выходом на наблюдение нужно провести еще техническую подготовительную работу:

• заготовить регистрационные листы (или бланки, схемы);

• точно знать, в какой форме будет вестись запись;

• проверить наличие записывающих средств;

• продумать ситуацию включения в наблюдение;

• определить место, с которого можно наилучшим образом увидеть то, что интересует;

• согласовать график наблюдений с ходом реальной жизни наблюда­емых людей-

Если в ходе наблюдения программа корректируется (например, до­полнены или изменены объекты наблюдения или состав испытуемых), то все эти изменения фиксируются письменно в журнале исследова­ний или дневнике наблюдений.

Обработка результатов наблюдений обусловлена его целями, вы­бранным видом и составленной программой. Если наблюдение прово­дится по формализованной схеме, то появляется возможность провес­ти первичную обработку, обобщая данные, полученные по каждому показателю, с учетом количества проведенных наблюдений. Вторич­ная обработка будет зависеть от задач исследования в целом.

Сложнее обстоит дело при обработке результатов наблюдения, ко­торое проводилось на основе фотографической записи и было сплош­ным. В этом случае исследователь должен проявить и теоретическую эрудицию, и интуицию для выделения линий анализа, по которым мо­гут быть сопоставлены полученные в разных наблюдениях факты. Если определить линии анализа, по которым выделяются общие и от­личительные признаки, зафиксированные в разных наблюдениях, то можно сделать обобщения и выводы из проведенных наблюдений. Вполне допустимо при этом использовать метод контент-анализа, ко­торый может помочь в выделении единиц (линий анализа) и основных семантических характеристик изучаемого явления. В этом случае целесообразно воспользоваться работами, посвященными технике контент-анализа текстов (31).

Поскольку метод наблюдения по сути своей направлен на изучение индивидуального, уникального в психике, он дает преимущественно качественные характеристики изучаемого явления. Как правило, дан­ные, полученные в наблюдении, не удается обрабатывать статистически в силу их небольшого количества.

Источник

Способы обработки результатов наблюдения

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

Государственная система обеспечения единства измерений

ПРЯМЫЕ ИЗМЕРЕНИЯ С МНОГОКРАТНЫМИ НАБЛЮДЕНИЯМИ.
МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ

State system for ensuring the uniformity of measurements.
Direct measurements with multiple observations.
Methods of processing the results of observations.
Basic principles

Дата введения 1977-01-01

УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ постановлением Государственного комитета стандартов Совета Министров СССР от 15 марта 1976 г. N 619

ПЕРЕИЗДАНИЕ. Август 1985 г.

Настоящий стандарт распространяется на нормативно-техническую документацию, предусмотренную ГОСТ 8.010-72 и регламентирующую методику выполнения прямых измерений с многократными независимыми наблюдениями, и устанавливает основные положения методов обработки результатов наблюдений и оценивания погрешностей результатов измерений.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. При статистической обработке группы результатов наблюдений следует выполнить следующие операции:

исключить известные систематические погрешности из результатов наблюдений;

вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;

вычислить оценку среднего квадратического отклонения результата наблюдения;

вычислить оценку среднего квадратического отклонения результата измерения;

проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению;

вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения;

вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;

вычислить доверительные границы погрешности результата измерения.

1.2. Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.

1.3. Для определения доверительных границ погрешности результата измерения доверительную вероятность принимают равной 0,95.

В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности =0,95, допускается указывать границы для доверительной вероятности =0,99.

В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо =0,99 принимать более высокую доверительную вероятность.

2. РЕЗУЛЬТАТ ИЗМЕРЕНИЯ И ОЦЕНКА ЕГО СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ

2.1. Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений.

Если результаты наблюдений можно считать принадлежащими к нормальному распределению, грубые погрешности исключают в соответствии с указаниями, приведенными в ГОСТ 11.002-73.

2.2. За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей.

Примечание. Если во всех результатах наблюдений содержится постоянная систематическая погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.

2.3. Среднее квадратическое отклонение результата наблюдения оценивают согласно разд. 1 ГОСТ 11.004-74.

2.4. Среднее квадратическое отклонение ( ) результата измерения оценивают по формуле

,

где — -й результат наблюдения;

— результат измерения (среднее арифметическое исправленных результатов наблюдений);

— число результатов наблюдений;

— оценка среднего квадратического отклонения результата измерения.

3. ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ СЛУЧАЙНОЙ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

3.1. Доверительные границы случайной погрешности результата измерения в соответствии с настоящим стандартом устанавливают для результатов наблюдений, принадлежащих нормальному распределению.

Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

3.1.1. При числе результатов наблюдений > 50 для проверки принадлежности их к нормальному распределению по ГОСТ 11.006-74 предпочтительным является один из критериев: Пирсона или Мизеса-Смирнова.

3.1.2. При числе результатов наблюдений 50> >15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий, приведенный в справочном приложении 1.

При числе результатов наблюдений 15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной настоящим стандартом, возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.

3.2. Доверительные границы (без учета знака) случайной погрешности результата измерения находят по формуле

,

где — коэффициент Стьюдента, который в зависимости от доверительной вероятности и числа результатов наблюдений находят по таблице справочного приложения 2.

4. ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ НЕИСКЛЮЧЕННОЙ СИСТЕМАТИЧЕСКОЙ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

4.1. Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности:

вызванные другими источниками.

В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

4.2. При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.

4.3. Границы неисключенной систематической погрешности результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле

,

где — граница -й неисключенной систематической погрешности;

— коэффициент, определяемый принятой доверительной вероятностью. Коэффициент принимают равным 1,1 при доверительной вероятности =0,95.

При доверительной вероятности =0,99 коэффициент принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех ( >4). Если же число суммируемых погрешностей равно четырем или менее четырех ( 4), то коэффициент определяют по графику зависимости (см. чертеж).

,

где — число суммируемых погрешностей;

; кривая 1-m = 2; кривая 2-m = 3; кривая 3-m = 4.

График зависимости

При трех или четырех слагаемых в качестве принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве следует принять ближайшую к составляющую.

Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.

5. ГРАНИЦА ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

5.1. В случае, если 8, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата .

Примечание. Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15%.

5.2. В случае, если неравенства п. 5.1 не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины в соответствии с п. 4.3. Если доверительные границы случайных погрешностей найдены в соответствии с разд. 3 настоящего стандарта, допускается границы погрешности результата измерения (без учета знака) вычислить по формуле

,

где — коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;

— оценка суммарного среднего квадратического отклонения результата измерения.

Источник