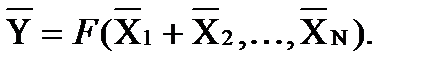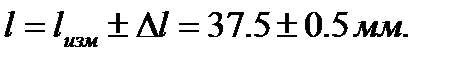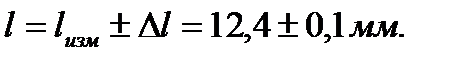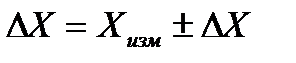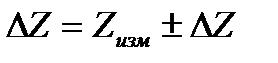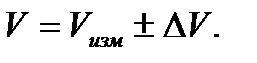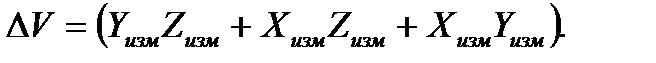Способы обработки результатов измерений

Способы обработки результатов измерений

ГОСТ Р 8.736-2011

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственная система обеспечения единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ МНОГОКРАТНЫЕ

Методы обработки результатов измерений. Основные положения

State system for ensuring the uniformity of measurements. Multiple Direct measurements. Methods of measurement results processing. Main positions

Дата введения 2013-01-01

Предисловие

1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им.Д.И.Менделеева» (ФГУП «ВНИИМ им.Д.И.Менделеева»)

2 ВНЕСЕН Управлением метрологии Федерального агентства по техническому регулированию и метрологии

4 ВВЕДЕН ВПЕРВЫЕ

5 ПЕРЕИЗДАНИЕ. Март 2019 г.

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

1 Область применения

Настоящий стандарт распространяется на прямые многократные независимые измерения и устанавливает основные положения методов обработки результатов этих измерений и вычисления погрешностей оценки измеряемой величины.

В настоящем стандарте учтены требования, предъявляемые к методам и результатам измерений в соответствии с ГОСТ Р ИСО 5725-1, ГОСТ Р ИСО 5725-2, ГОСТ Р ИСО 5725-3, ГОСТ Р ИСО 5725-4, ГОСТ Р ИСО 5725-5, ГОСТ Р ИСО 5725-6.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р ИСО 5725-1 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения

ГОСТ Р ИСО 5725-2 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

ГОСТ Р ИСО 5725-3 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений

ГОСТ Р ИСО 5725-4 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений

ГОСТ Р ИСО 5725-5 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений

ГОСТ Р ИСО 5725-6 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены следующие термины с соответствующими определениями.

результат измерения физической величины; результат измерения; результат: Значение величины, полученное путем ее измерения.

[Рекомендации по межгосударственной стандартизации [1], статья 8.1]

3.2 неисправленный результат измерений величины: Результат измерений величины, полученный до введения в него поправки в целях устранения систематических погрешностей.

3.3 исправленный результат измерений величины: Результат измерений величины, полученный после введения поправки в целях устранения систематических погрешностей в неисправленный результат измерений величины.

3.4 неисправленная оценка измеряемой величины: Среднее арифметическое значение результатов измерений величины до введения в них поправки в целях устранения систематических погрешностей.

3.5 исправленная оценка измеряемой величины: Среднее арифметическое значение результатов измерений величины после введения поправки в целях устранения систематических погрешностей в неисправленную оценку измеряемой величины.

3.6 группа результатов измерений величин: Несколько результатов измерений (не менее четырех, 4), полученных при измерениях одной и той же величины, выполненных с одинаковой тщательностью, одним и тем же средством измерений, одним и тем же методом и одним и тем же оператором.

3.7 погрешность измерения: Разность между результатом измерения величины и действительным (опорным) значением величины.

3.8 случайная погрешность измерения; случайная погрешность: Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.

3.9 систематическая погрешность измерения; систематическая погрешность: Составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью.

3.10 неисключенная систематическая погрешность измерения: Составляющая погрешности измерения, обусловленная погрешностью оценивания систематической погрешности, на которую введена поправка, или систематической погрешностью, на которую поправка не введена.

3.11 грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей.

4 Общие положения

4.1 Необходимость выполнения прямых многократных измерений устанавливают в конкретных методиках измерений.

Примечание — Под многократными измерениями понимают не менее четырех измерений.

4.2 При статистической обработке группы результатов прямых многократных независимых измерений выполняют следующие операции:

— исключают известные систематические погрешности из результатов измерений;

— вычисляют оценку измеряемой величины;

— вычисляют среднее квадратическое отклонение результатов измерений;

— проверяют наличие грубых погрешностей и при необходимости исключают их;

— проверяют гипотезу о принадлежности результатов измерений нормальному распределению;

— вычисляют доверительные границы случайной погрешности (доверительную случайную погрешность) оценки измеряемой величины;

— вычисляют доверительные границы (границы) неисключенной систематической погрешности оценки измеряемой величины;

— вычисляют доверительные границы погрешности оценки измеряемой величины.

4.3 Проверку гипотезы о том, что результаты измерений принадлежат нормальному распределению, проводят с уровнем значимости от 10% до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике измерений.

4.4 Для определения доверительных границ погрешности оценки измеряемой величины доверительную вероятность принимают равной 0,95.

В случаях, когда измерение не представляется возможным повторить, помимо границ, соответствующих доверительной вероятности 0,95, допускается указывать границы для доверительной вероятности 0,99.

В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается кроме доверительной вероятности 0,99 указывать более высокую доверительную вероятность.

4.5 В настоящем стандарте изложены требования к методам обработки результатов измерений и к оцениванию точности измеряемой величины посредством погрешностей.

5 Оценка измеряемой величины и среднее квадратическое отклонение

5.1 Оценку измеряемой величины , за которую принимают среднее арифметическое значение исправленных результатов измерений, вычисляют по формуле

, (1)

где — -й результат измерений;

— число исправленных результатов измерений.

Примечание — Если во всех результатах измерений содержится постоянная систематическая погрешность, ее допускается исключить из вычисленного среднего арифметического значения неисправленных результатов измерений.

5.2 В целях удобства вычислений формулу (1) допускается записать в виде

, (2)

где — близкое к значение, удобное для расчета;

.

5.3 Среднее квадратическое отклонение группы, содержащей результатов измерений, вычисляют по формуле

. (3)

Примечание — Наличие случайных погрешностей вызывает рассеяние результатов измерений. В качестве основной числовой характеристики случайного рассеяния результатов измерений принята дисперсия или стандартное отклонение . Ограниченное число результатов измерений позволяет получать лишь оценки этих характеристик ( и ). Математическое ожидание оценки равно дисперсии , однако математическое ожидание оценки отлично от , так как оценка смещена.

Несмещенную оценку допускается вычислять по упрощенной формуле

.

Источник

Основы измерений и обработки результатов

Цель работы: знакомство с элементами теории погрешностей, методами измерения основных физических величин и правилами обработки результатов измерений.

Основные теоретические положения

(элементарные представления теории погрешностей)

Измерением называется процедура определения действительного значения физической величины с помощью специальных технических средств. Указанная процедура состоит из нескольких этапов: выбора измеряемой величины, метода измерения, приборов для наблюдения, метода обработки результатов наблюдения. Поэтому результаты наблюдения, как правило, не дают истинного значения измеряемой величины, то есть они содержат погрешности измерений.

По способу получения результата все измерения делятся на прямые и косвенные. Измерение, при котором значение физической величины находится непосредственно из опытных данных, называется прямым измерением – это, например, измерение температуры термометром, длины – линейкой.

Измерение, при котором искомое значение физической величины вычисляют по формуле на основании известной зависимости между ней и величинами, получаемыми при прямых измерениях, называется косвенным измерением, − например, измерение плотности тела по его массе и геометрическим параметрам, сопротивление проводника по напряжению и току.

Погрешность измерения – это отклонение результата измерения от истинного значения, которое может быть получено с помощью более совершенных методов и средств измерений. Различают абсолютную и относительную погрешности.

Абсолютная погрешность ΔX равна разности между результатом измерения X и истинным или точным значением измеряемой величины:

. (1.1)

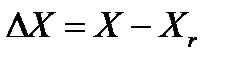
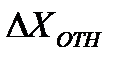
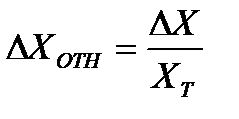
Относительная погрешность измерения представляет собой отношение абсолютной погрешности к истинному или точному значению измеряемой величины:

(1.2)

Погрешности измерения имеют случайную и систематическую составляющие.

Составляющая погрешности измерения, которая случайным образом изменяется при повторных измерениях одной и той же величины, называется случайной погрешностью. Случайная погрешность определяется факторами, проявляющимися нерегулярно с изменяющейся интенсивностью. Значение случайной составляющей невозможно предвидеть, следовательно, исключить.

Случайная погрешность прямых измерений вычисляется следующим образом:

. (1.3)

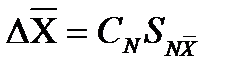
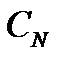
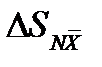
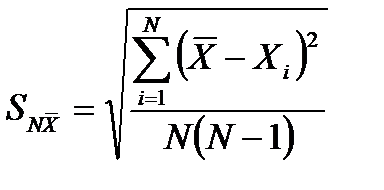
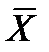
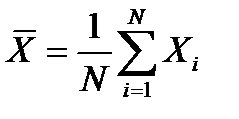
Здесь − коэффициент Стьюдента, − среднее квадратичное отклонение, вычисляемое по формуле

, (1.4)

а − среднее значение измеряемой величины

. (1.5)

Результат измерения представляется в виде

.

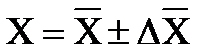
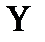
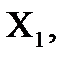
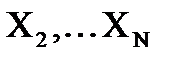
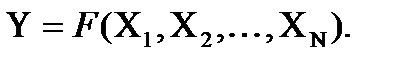
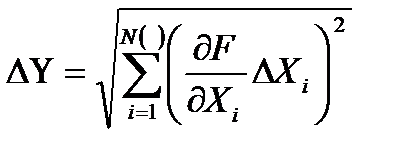
Для нахождения предельной случайной абсолютной погрешности косвенных измерений в том случае, когда интересующая экспериментатора величина связана с несколькими измеряемыми величинами функциональной зависимостью

(1.6)

. (1.7)

Предельная относительная погрешность рассчитывается по формуле:

. (1.8)

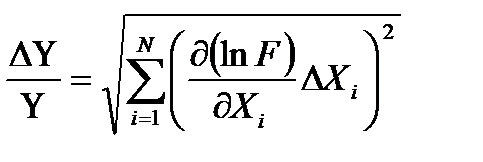
Результат измерения представляется в виде

, (1.9)

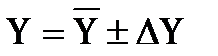
где

Отдельные результаты измерений могут сильно отличаться от среднего значения, что вызывается кратковременным и сильным воздействием какого-либо внешнего фактора. Возникающая при этом погрешность называется промахом. Ошибочный результат наблюдения в этом случае должен быть исключен при обработке результатов измерения.

Погрешности, которые при повторных измерениях остаются постоянными или закономерно изменяются, называются систематическими. Их можно оценить или исключить из результатов измерений путем введения поправок.

Систематические погрешности классифицируются следующим образом:

1. Систематические погрешности, о существовании которых ничего не известно, но которые могут иметь значительную величину.

Такие погрешности проявляются при сложных измерениях и их почти никогда не удается устранить. Измерение с такой ошибкой является неверным.

2. Погрешности известного происхождения, но неизвестной величины, которые не могут быть исключены, но могут учитываться в конечном результате. Наиболее распространенной погрешностью такого типа является погрешность измерительных приборов, определяемая классом его точности.

3. Систематические погрешности, природа которых известна, а их величина может быть установлена более или менее точно. Для устранения таких погрешностей в измерения вводятся поправки.

Различают систематические погрешности прямых и косвенных измерений. Систематическая погрешность прямого измерения – это, как правило, величина погрешности при нормальных условиях эксплуатации средства измерения.

В случае применения нескольких средств измерений, образующих комбинированное устройство, возникает систематическая погрешность косвенных измерений, предельная величина которой рассчитывается по формуле, аналогичной (1.7):

, (1.10)

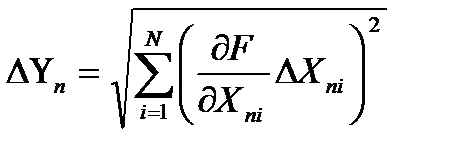
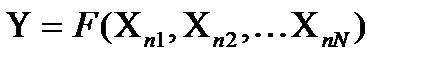
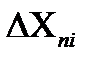
где функция , − систематическая погрешность каждого отдельно взятого измерительного средства, входящего в устройство.

В большинстве случаев результаты эксперимента содержат и систематические, и случайные погрешности. Поэтому целесообразно организовать эксперимент таким образом, чтобы исключить одну из них. Для этого можно использовать следующие правила:

1. Если систематическая погрешность значительно больше случайной, то нет смысла уменьшать случайную погрешность, увеличивая число экспериментов, и достаточно осуществить наблюдение один раз.

2. Если случайная погрешность является определяющей, то для уменьшения число наблюдений следует выбирать таким, чтобы случайная погрешность среднего арифметического была меньше систематической погрешности. В этом случае результирующая погрешность определяется, в основном, систематической погрешностью.

3. Если в эксперименте присутствуют систематические погрешности неизвестного типа и большой величины, то их можно устранить, организовав измерение таким образом, чтобы постоянный фактор, вызывающий систематическую погрешность, в каждом из наблюдений действовал различным образом. В результате такой организации эксперимента постоянно действующий фактор становиться случайным, а систематическая погрешность превращается в случайную. Этот прием называется рандомизацией и позволяет практически исключить многие неизвестные погрешности.

Если все же не удается обеспечить исключение погрешности, какого–либо типа, то при обработке результатов эксперимента возникает необходимость суммирования погрешностей.

В простейшем случае величина предельной суммарной погрешности прямых измерений вычисляется по формуле

, (1.11)

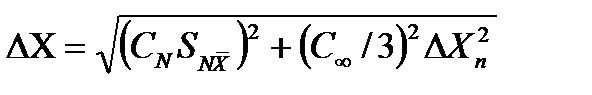
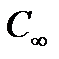
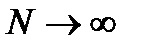
где − значение коэффициента Стьюдента при .

Величина предельной суммарной погрешности косвенных измерений рассчитывается по формуле

. (1.12)

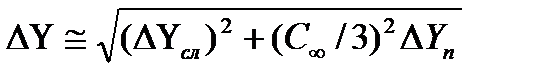
Все измерения осуществляются с помощью средств измерений – технических устройств, имеющих нормированные метрологические характеристики. Применяемые на практике средства измерений подразделяют на измерительные приборы, измерительные преобразователи, измерительные установки и измерительные системы.

Важнейшей характеристикой средств измерений является их точность, которая характеризуется соответствующими составляющими погрешности результата измерений.

Погрешность средств измерений – это метрологическая характеристика, количественно выражающая отклонение номинального значения физической величины, воспроизводимой или измеряемой данным средством измерений, от истинного или точного значения.

Различают абсолютную, относительную и приведенную погрешности измерительных приборов.

Абсолютная погрешность прибора есть разность между показанием прибора А и истинным значением измеряемой величины , то есть

(1.13)

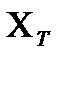
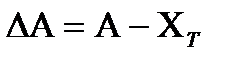
Относительная погрешность представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины:

. (1.14)

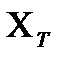
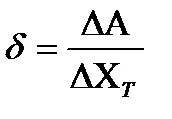
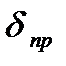
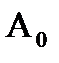
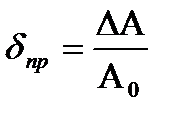
Приведенная погрешность есть отношение абсолютной погрешности к нормирующему значению , то есть условно принятому значению физической величины, постоянному во всем диапазоне измерений или некоторой его части:

. (1.15)

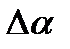
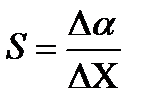
Важной эксплуатационной характеристикой прибора является чувствительность S, то есть отношение изменения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины:

. (1.16)

Величина, обратная чувствительности 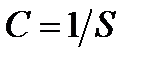, называется ценой деления прибора.

Более подробно указанные характеристики описаны для электроизмерительных приборов в лабораторной работе 11 настоящего руководства.

Описание лабораторной установки и последовательность проведения измерений

Установка представляет собой специальный ящик, в котором представлен набор измерительных инструментов: линейка, штангенциркуль, микрометр, транспортир, секундомер, термометр, а также исследуемые объекты: параллелепипед, неравноугольный треугольники сосуд с нагревателем.

Задание 1. Измерение линейных размеров с помощью линейки, штангенциркуля и микрометра.

1. Однократные измерения размера линейкой.

Линейка является простейшим измерительным устройством. Цена деления линейки может быть различной. Для измерения с помощью линейки необходимо нулевую отметку

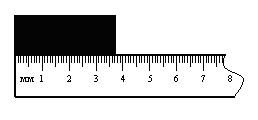
Рис. 1.1. Линейка

шкалы совместить с краем измеряемого отрезка.

Результат измерения считывается по шкале линейки по другому краю измеряемого отрезка.

Погрешность измерения с помощью линейки составляет не более ½ цены ее наименьшего деления. Доли наименьшего деления считываются на глаз с точностью, не превышающей погрешность измерения, то есть 0,5 цены деления.

Пример 1. По линейке с ценой деления 1 мм произведен отсчет 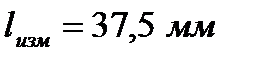. Результат измерения записывается так:

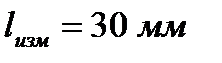
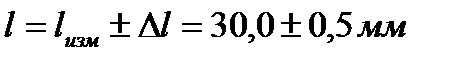
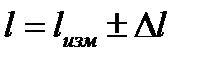
Пример 2. Той же линейкой измерен размер . Результат измерения записывается следующим образом: При выполнении этого задания проводятся однократные измерения размера любого предмета линейкой, например, размер грани параллелепипеда или стороны треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: , (см. примеры 1 и 2).

2. Однократные измерения штангенциркулем.

Штангенциркуль представляет собой металлическую линейку 1, на конце которой имеется поперечный выступ 2. Другой такой же выступ имеется на обойме 3. Они движутся по линейке. Обойма имеет окно 4, позволяющее видеть основную шкалу линейки. Внутренние поверхности 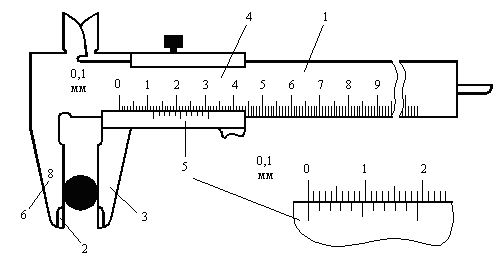выступов строго перпендикулярны линейке. Когда они прилегают друг к другу, указатель «нуль» на обойме находится против нулевого деления шкалы линейки. Измеряемый предмет зажимается между выступами.

Рис. 1.2. Штангенциркуль

Для измерения внутренних размеров от­верстий наружные стороны концов выступов обычно делаются строго перпендикулярными линейке и слегка закругляются. Расстояние между ними при установке обоймы на нуль шкалы (обычно 8 или 10 мм) указывается на штангенциркуле 6. Иногда для измерения внутренних размеров делаются специальные ножи на тыльной стороне выступов, концы выступов заостряются. Такое устройство позволяет измерять отверстия малых размеров, но точность измерения при этом меньше.

Достаточно высокая точность измерения штангенциркулем достигается с помощью нониуса. Нониус – это дополнительная линейка со шкалой 5, нанесенной по краю подвижной 3.

Нулевой штрих шкалы нониуса служит одновременно указателем для считывания числа целых делений по основной шкале и началом отсчета долей миллиметра по шкале нониуса. Обычно число делений нониуса n = 10 или n=20.При 10 делениях нониуса всей длине его шкалы соответствует 19мм основной шкалы, то есть 10 делений нониуса имеют длину, на 1 мм меньшую, чем 20 делений основной шкалы. Цену деления нониуса штангенциркуля можно найти по формуле 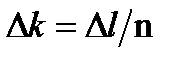. 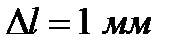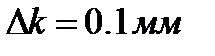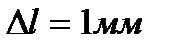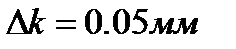При 10 делениях нониуса и . При 20 делениях нониуса . Погрешность градуировки штангенциркуля при n = 10 равна 0,1 мм, а при n = 20 равна 0,05 мм.

Пример 3.Нониус штангенциркуля имеет цену деления 0,1 мм. Число целых делений шкалы до нуля нониуса – 12. Штрих основной шкалы совпадает со штрихом шкалы нониуса, которому предшествует 4 деления его шкалы. Результат отсчета 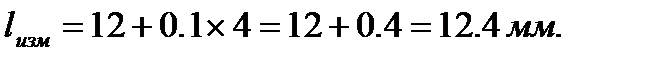Результат измерения записывается в виде:

При выполнении этого задания проводятся однократные измерения размера любого предмета штангенциркулем, оцениваются погрешности измерения и результат представляется в виде 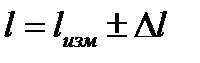(см. пример 3).

3. Однократные измерения размера микрометром.

Для измерения внешних размеров предметов с большой точностью, чем штангенциркулем, служит микрометр. Он состоит из скобы 1, жестко соединенной с измерительным упором 2, цилиндра 3, барабана 4, который соединен с микрометрическим винтом и подвижным измерительным упором 5. На цилиндре 3 нанесено 2 миллиметровых шкалы: нижняя – основная, верхняя – дополнительная, смещенные относительно друг друга на 0,5 мм. Левый конусный конец барабана имеет круговую шкалу 6, состоящую из 50 делений. Шаг микрометрического винта равен 0,5 мм, поэтому один оборот барабана соответствует изменению линейного размера 0,5 мм.

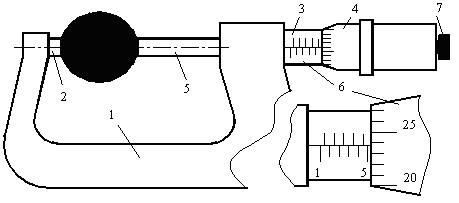
Рис. 1.3. Микрометр

Измеряемый предмет помещают между винтом 5 и противоположным ему упором 2 так, как показано на рисунке 1.3. Винт вращают и доводят до соприкосновения с предметом. При измерении микрометром существенно постоянство вращательного момента, приложенного к барабану при соприкосновении упоров с измеряемым предметом. Поэтому барабан 4 следует вращать, прикладывая усилие не к нему самому, а к головке 7. Она соединяется с винтом с помощью «трещотки», которая передает усилие только до тех пор, пока она не достигнет определенной величины. Когда же эта величина достигнута, дальнейшее вращение головки происходит в «холостую» и не изменяет показания микрометра.

Результат измерения получают в следующем порядке. Сначала производят отсчет размера по основной и дополнительным шкалам с точностью до 0,5 мм, после этого осуществляется отсчет сотых долей миллиметра по шкале барабана и результаты суммируются.

Погрешность градуировки микрометров составляет 0,004 мм.

Пример 4. На основной шкале видно 5 целых миллиметровых делений. Следующая справа за меткой 5 основной шкалы отметка дополнительной шкалы не видна. Отсчет по шкале барабана – 24.

Результат отсчета . Результат измерения: .

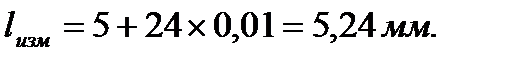
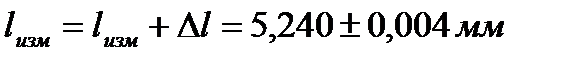
При выполнении этого задания проводятся однократные измерения размера любого предмета микрометром, оценивается погрешность и результат представляется в виде: 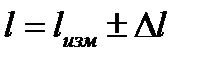(см. пример 4).

4. Повторное измерение размеров

Повторные измерения предметов являются прямыми наблюдениями. Процедура их осуществляется очень просто: одним и тем же измерительным инструментом – линейкой, штангенциркулем или микрометром измеряют один и тот же размер несколько раз через определенный интервал времени, и результаты заносятся в таблицу.

Обработка результатов эксперимента.

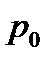
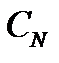
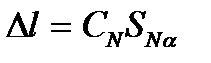
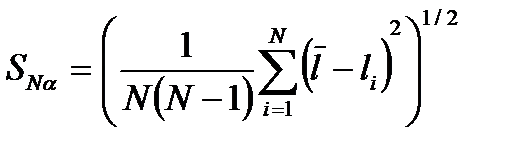
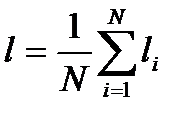
1. Погрешность величины l в каждом измерении отдельным измерительным инструментом находится по методике расчета погрешностей прямых измерений, задавая доверительную вероятность и коэффициент Стьюдента .

, (1.17)

, (1.18)

. (1.19)

2. Погрешность смешанных измерений вычисляется аналогично:

(1.20)

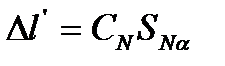
Сравниваются погрешности 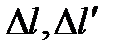и объясняются расхождения.

Задание 2. Измерение объема параллелепипеда.

Такие измерения являются косвенными и их можно осуществить двумя способами.

Способ 1. Однократные измерения

Одним из измерительных инструментов один раз определяется длина одной грани параллелепипеда и результат записывается в виде:

(1.21)

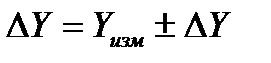
Обработка результатов эксперимента.

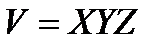
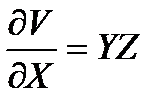
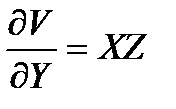
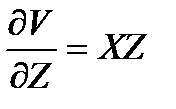
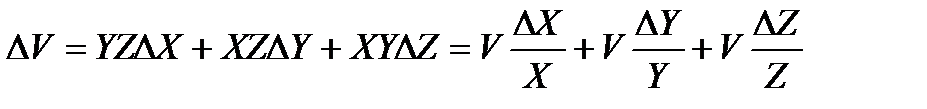
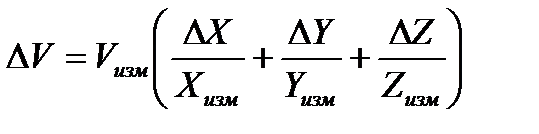
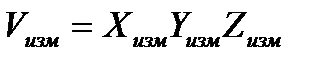
1. Погрешность однократных косвенных измерений различными инструментами рассчитывается по формуле (1.10). Так как объем , то

, , ,

,

,

. (1.22)

Результат измерения представляется в виде

2. В том случае, если длина всех граней измерена одним и тем же инструментом с одинаковой погрешностью 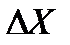,то

Способ 2. Повторные измерения

Осуществляются повторные измерения любым измерительным инструментом одной грани несколько раз, и результаты заносятся в таблицу.

Обработка результатов эксперимента.

Вычисляется среднее значение объема 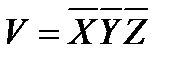и погрешность

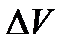
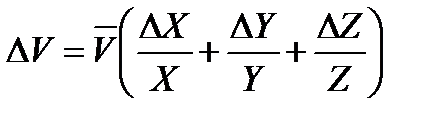
его определения по формуле (1.22):

, (1.23)

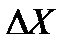
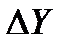
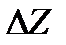
где , , вычисляют по методике расчета погрешностей прямых измерений.

Любопытно провести эти измерения, используя для получения результата различные измерительные инструменты, вычислить погрешность и сравнить значения объема и погрешности, полученные при измерении линейкой, штангенциркулем и микрометром, а также при смешанных измерениях.

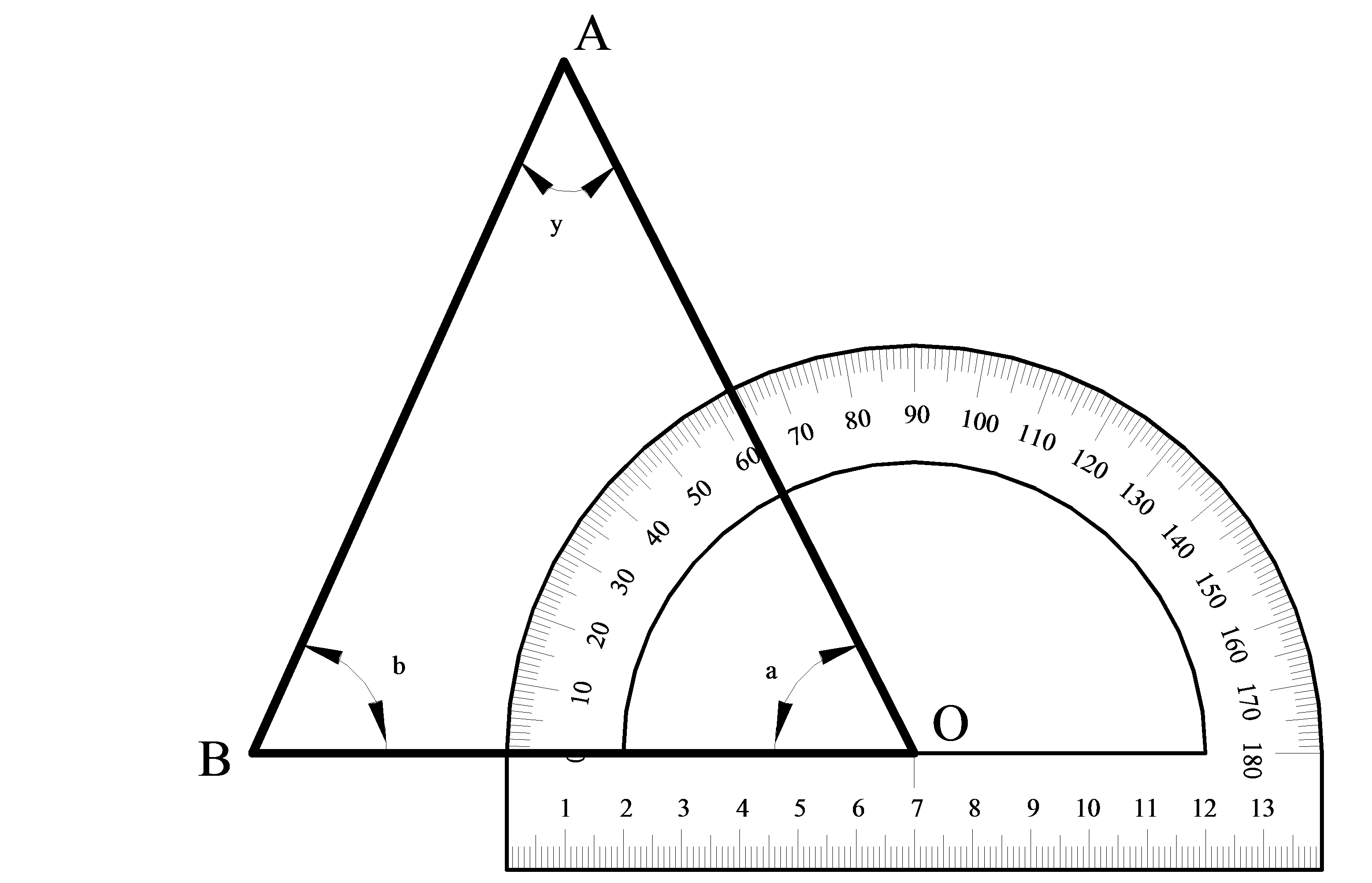
Задание 3. Измерение плоских углов транспортиром.

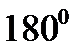
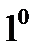
Для простейших измерений углов применяется транспортир, который представляет собой полукруг, дуга которого разделена на через . Чтобы измерить угол у, накладывают транспортир (рис. 1.4) так, чтобы вершина угла совпала с центром полукруга, а стороны – с радиусами ОА и ОВ. Тогда число градусов, содержащихся в дуге, заключенной между сторонами угла АОВ, дает числовое значение его величины. Погрешность измерения углов по транспортиру составляет половину деления шкалы – 0,5.

Рис. 1.4. Транспортир

Пример 5. Результат отсчета по шкале транспортира 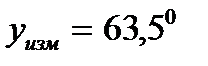. Результат измерения

Более сложные и более точные приборы для измерения углов мы не рассматриваем.

1. Однократное измерение углов.

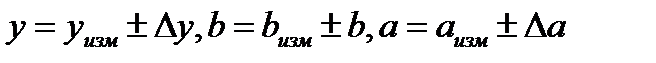
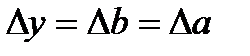
При выполнении этого задания проводятся однократные измерения углов треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: , причем очевидно, что .

2. Многократные измерения углов.

Погрешности величин у, b, а находятся по формуле расчета погрешностей прямых измерений:

. (1.26)

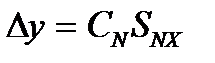
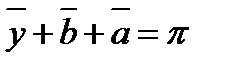
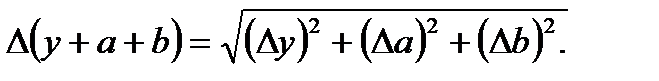
И в первом, и во втором случае можно проверить результат, используя формулу . При этом погрешность суммы углов отличается от погрешности измерения отдельного угла и вычисляется по формуле

(1.27)

Задание 4. Измерение времени секундомером.

Для измерения времени применяются секундомеры. Механические секундомеры имеют цену деления 0,1 и 0,2 с.

Основная погрешность этих секундомеров равна цене деления, а погрешность отсчета зависит от быстроты реакции на включение и остановку секундомера. Установлено, что неточности пуска и остановки дают погрешность порядка 0,3 с. Таким образом, при работе с секундомером с ценой деления 0,2 с погрешность может достигать 0,5 с.

Применяются электронные секундомеры с ценой деления 0,01 и 0,001 с. Их целесообразно использовать вместе с устройствами, обеспечивающими совпадение пуска и остановки с началом и концом процесса, длительность которого определяется.

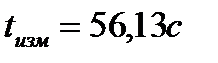
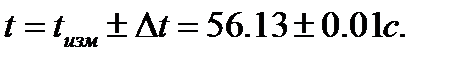
Пример 6. По индикатору электронного секундомера с ценой деления 0,01 с зарегистрировано некоторое время . Результат измерения Методика измерения интервалов времени и обработки результатов при однократных и повторных измерениях та же, что и в предыдущих заданиях по измерению линейных размеров и углов.

Задание 5. Измерение температуры термометром.

Термометр представляет собой капиллярную трубку из стекла, которая заполнена жидкостью, обычно ртутью или подкрашенным спиртом. Капиллярная трубка помещена в корпус из стекла, в котором также закреплена измерительная шкала. Погрешность измерения температуры термометрами различных типов регламентируется ГОСТ 400-80 и имеет, в большинстве случаев, величину, равную цене деления.

Методика измерения температуры и обработки результатов при однократных и многократных измерениях та же, что и в предыдущих заданиях.

Источник