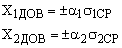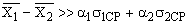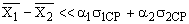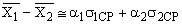- Обработка результатов эксперимента.
- Способы обработки результатов экспериментов
- XI. МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
- 11.1. ПОДГОТОВКА ПЕРВИЧНЫХ ДАННЫХ К АНАЛИЗУ
- 11.2. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЕДАГОГИЧЕСКИХ ОБЪЕКТОВ
- 11.3. СОДЕРЖАТЕЛЬНЫЙ АНАЛИЗ ДАННЫХ И ПОЛУЧЕНИЕ ВЫВОДОВ
- 11.4. ДОСТОВЕРНОСТЬ РЕЗУЛЬТ А ТОВ
- Р ек о мендуемая литер а тура
- Дополнительная л и т ература
Обработка результатов эксперимента.
В конце представляется отчёт; для представления отчёта по теме проводятся эксперименты; данные должны быть в виде формул, экспериментальные данные необходимо обработать. Смысл обработки в том, чтобы выяснить, правильно ли проведён эксперимент.
Существует 2 этапа обработки результата:
1. Выявление связей параметров. Проводится выявление наличия зависимости одного фактора от другого (входные воздействия и отклики). Как правило, общий вид закономерности известен из литературы. Когда имеется много воздействий, проводится специальный вид анализа – корреляционный анализ.
2. Определение погрешностей.
Способ обработки результатов эксперимента:
1. Запись результатов измерения .
2. Вычисление среднего значения из N измерений
3. Определение погрешности отдельных измерений
4. Вычисление квадратичной погрешности отдельных измерений 
5. Если несколько измерений резко отличаются от остальных, следует проверить, не являются ли они промахами. Эти промахи исключаются и повторяются пункты 1-4
6. Определяется среднеквадратичная погрешность результата серии измерений:
7. Задаётся значение коэффициента надёжности α.
8. По надёжности определяется коэффициент Стьюдента tα(n).
9. Находятся границы доверительного интервала
10. Если величина погрешности результата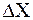 
оказывается сравнима с величиной приборной погрешности, то в качестве границы доверительного интервала следует взять величину:
11. Записывается окончательный результат.
12. Считается относительная погрешность:
Смысл такой проверки в том, что если измерение проведено корректно, то существует какое-то среднее значение, около которого по Гауссовой кривой и будут распределяться значения результата.
Большинство измерений (с определённым α) будут находиться в интервале ±ΔХ. Если во время измерений не учтена погрешность, то график кривой будет деформирован. Если же построение корректно, то все отклонения значения от истинного значения будут носить случайный характер и распределяется по нормальному закону.
Если сделан вывод, что результат корректен, то можно переходить к следующему этапу – построению регрессионных моделей.
Регрессия – описание экспериментальных данных некоторой зависимостью (формулой) для нахождения численных коэффициентов, которые характеризуют некоторые параметры протекающих в образце процессов. Т.о. экспериментальную кривую мы пытаемся описать какой-то простой кривой.
Измерения бывают прямые и косвенные.
Прямые – на выходе получается измерительный параметр – измерение путём сравнения с образцом.
Косвенные – измерение искомого параметра путём измерения сопутствующего параметра. Косвенные измерения содержат больше ошибок и погрешностей.
У цифрового прибора последняя цифра всегда неверна (она не определяется, а отбрасывается).
1. Систематические – обусловлены какими-либо дефектами прибора или постоянными внешними воздействиями; они присутствуют в приборе всегда; все измерительные периодически проходят поверку; есть специальные правила, нормы, таблицы по данному прибору – о времени поверки и др.
2. Случайные – возникают из-за множества причин; такие ошибки в прямом эксперименте невозможно устранить. Но если число измерений увеличивается в N раз, то погрешность уменьшается в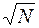 
раз. Т. о. случайные ошибки можно свести к нулю.
3. Промахи (грубые ошибки).
Самые точные приборы – стрелочные – по ним поверяют цифровые приборы, так как микросхемы могут ошибаться, могут стареть, могут получать дефекты, а в стрелочных используются дискретные элементы, их легко проверить, они более механически прочные.
Обычно у стрелочных приборов первая 1/3 и последняя 1/10 шкалы более неточные. Там результаты такие, что необходимо переключать прибор на другие пределы измерений. Такие значения нужно перемеривать, чтобы исключить ошибки. Поверку приборов проводит специальный отдел – ОГМЕТР.
Систематические и грубые ошибки можно устранить, а случайные свести к нулю путём увеличения числа измерений.
Свойства случайных ошибок:
1. Число отклонений в большую сторону равно числу отклонений в меньшую сторону.
2. Мелкие отклонения встречаются гораздо чаще, чем крупные (Гауссова кривая).
3. Величина самых крупных отклонений ограничена по размеру и её, как правило, называют предельной ошибкой.
4. Если просуммировать все случайные ошибки, то сумма равна нулю при большом числе измерений.
Регрессия – это когда массив данных описывается какой-то математической кривой. Когда строится зависимость, то все влияние всех несущественных параметров отбрасывается. Сложная зависимость сводится к более простой.
Аппроксимация – описание массива данных какой-либо известной формулой, которая ставит целью определение численных коэффициентов. Главное отличие аппроксимации от регрессии – то, что формула имеет какой-то физический смысл, по полученным коэффициентам можно судить о протекающих внутри чего-либо процессах.
Одним из самых эффективных методом регрессии считается сплайн-регрессия – между соседними точками строятся отрезки степенной функции (кубическая сплайн-регрессия, полиномы от 2-й до N-й степени, сплайн бывает параболическим).
1. Графический способ – самый старый – строится график функции и его сравнивают с набором заранее построенных кривых, шаблонов. Недостаток этого метода – субъективность, поэтому все построения нужно проводить с использованием специальных компьютерных программ.
2. Способы приведения сложных кривых к линейному виду:
Пример: способ функциональных шкал (вместо у на шкале ставится ln(у) или а/у (а – коэффициент)). Функциональные шкалы используют для того, чтобы привести зависимость сложного вида к линейному виду.
3. Аналитические методы:
Пример: компьютерный подбор; в MathCAD – «Регрессия общего вида». Заключается в том, что в ЭВМ вводится массив исходных данных – координаты экспериментальных точек по х и по у, и аналитическая зависимость (формула с неизвестными коэффициентами). Компьютер путём подбора неизвестных коэффициентов пытается наиболее точно описать массив исходных данных.
Для того чтобы ускорить подбор коэффициентов строится пространство коэффициентов, показывается разница между реальным и вычисленным компьютером значениями. В зависимости от положения точек относительно экспериментальных значений определяется, в какую сторону изменять подбираемые коэффициенты для уменьшения погрешностей (существует много алгоритмов на ЭВМ).
Трудность аналитических методов.
Один и тот же набор экспериментальных точек может быть описан какой-либо кривой с различным набором коэффициентов, т. е. компьютеру всё равно, какие коэффициенты подобрать, а физического смысла нет, значит, начальную кривую надо задавать так, чтобы компьютер выдавал результат, имеющий физический смысл.
Источник
Способы обработки результатов экспериментов
Нет хороших и плохих методов,
есть хорошее и плохое их применение.
XI. МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
11.1. ПОДГОТОВКА ПЕРВИЧНЫХ ДАННЫХ К АНАЛИЗУ
Наблюдая и измеряя характеристики объекта, экс п ериментатор собирает первичный статистический материал. Дальнейшая за д ача состоит в такой обработке и представлен и и п е рвич н ых д ан ных, которые позволил и бы о ц е н ить и сопоставить р е зультаты для проверки гипотез, для выявле н ия существенных свойств и законо мерностей педагогического про ц есса. В основе методов обработки л е жит предварительно е у п орядочение, cиcтeмaтиaция первичных да н ных и вычисление их ста т истически х х а ракт е р и стик.
Обобщенный алгоритм подготовки данных может быть представлен следующим операциями:
а) все данные формулируются и записываются в необход и мо й краткой форме;
б) проводится группировка данн ых, то есть распределен и е их на однородные группы в соответств и и с интер е сую щи м и экспери ментатора признаками. Данные в каждой гру п п е упорядочиваются — классифи ц ируются, сортируются, структур и руются в соответствии с той модел ь ю, которая разрабатыв а лас ь п ри составлении п лана-программы (линейный, параллел ьный или перекрестный эксперимент);
в) устанавливаются характеристи ки (пр и з н ак и, п араметры каждой группы данных и производится подсч е т абсолют н ого числа факторов, характеризующих груп п у (число учащихся, уроков, отметок, ответов и т.д.);
г) дан н ые внутри каждой сформ и рованной группы располагаются в ряд (вариационный ряд) по убыванию или возрастанию п ризнака. Определяется наиболь ш ее и н аименьшее значения признака;
д) вариацио н ные ряды данных, получе н ных в номинальной ил и порядковой шкале, ранжируются . Интервалы группировки по рангам выбираются оптимальными (слишком кр уп ные интервалы скрывают нюансы явлений, сли ш ком дробные — затрудняют o6pаботку ). В результате этой операци и появляются н овые количест венные данные;
е) проводится статистическая обработка полученных количественных данных, заключающаяся в вычислении некоторых статистических характероистик и оц е нок, позволяющ и х глубже понять особенности экспериментальных я влений;
ж) составляются наглядные материалы, отображающие полученную информац ию: таблицы, графики, диаграммы, схемы и др., по ко то р ы м в дальнейшем у с т а н авлива ютс я и анализируются связи между параметрами эксперим е нтал ьных объектов.
11.2. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЕДАГОГИЧЕСКИХ ОБЪЕКТОВ
Педагогические явления относятся к числу массовых: они охватывают большие совокупности людей, повторяются из года в год, совершаются непрерывно. Показатели (параметры, результаты) педагогического процесса имеют вероятностный характер: о д но и то же педагогическое воздействие может приводить к различным следствиям (случайные события ). Тем не менее, при много к ратном вос п роиз в е дении ус ловий определенные следствия появляются чаще других, — это и есть проявление так н азываемых статистич е ских закономерностей (изучением которых занимаются теория вероятностей и математическая статистика).
Методы математической статистики в последние десятилетия стали применяться и в педагогике. Поэтому экспериментатору необходимо знание ряда простейших понятий математической статистики и умение с ними работать.
Все множество интересующих исследователя однородных явлений, событий или их показателей называется генеральной совокупностью данных объектов. Та часть последней, которая подвергается экспериментальному изучению, называется выборочными совокупностью или выборкой.
Величина (объем) выборки представляет собой абсолютное (счетное) количество однородных объектов исследования (явлений, событий или их характеристик).
Выборка характеризуется рядом статистических характеристик, наиболее употребительными из которых являются: относительное (процентное) значение, удельное значение, среднее арифметическое значение, дисперсия, среднее квадратичное отклонение среднего арифметического.
Относительное значение данного показателя — это отношение числа объектов, имеющих этот показатель, к величине выборки. Выражается относительным числом или в процентах (процентное значение).
Пример: Успеваемость в классе = числу положительных итоговых отметок, деленному на число всех учащихся класса. Умножение этого значения на 1 00 дает успеваемость в процентах.
Удельное значение данного признака — это расчетная величина, показывающая количество объектов с данным показателем, которое содержалось бы в условной выборке , состоящей из 1 0, или 100, 1 000 и т. д. объектов.
Пример: Для сравнения уровня правонарушений в разных регионах берется удельная величина — количество правонарушений на 1000 человек (N)
N = (число правонарушений в регионе)*1000
( население региона)
Среднее значение данного показателя выборочной сово купности (арифметическое среднее, выборочное среднее) — это отношен и е суммы всех измеренных значени й показателя к велич и н е в ыборки.
(1)
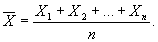
Средн е е значение недостаточно полно характеризует выборку; за ним скрывается “поведение” самого по к азателя явления — “разброс” , разл и чное распределение его значений около с реднего (так называемая “функция распределения”).
Пример: Наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Среднее значение посещаемости в обоих классах получается одинаковое — 19. Однако видно, что в контрольном классе этот показатель подчинен воздействию каких-то специфических факторов.
Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и среднего квадратичного отклонения.
Дисперсией (d 2 ) статистического показателя называется среднее значение квадратов отклонений отдельных его значений от среднего выборочного; дисперсия определяется по формуле:
(2)
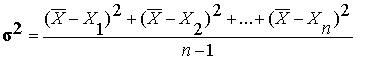
Ср едн и м квадратическим отклонением (экспе рим ен тальн ы м) называется к о р е нь кв ад ратный из диспер си и.
(3)
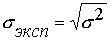
Пример: Для предыдущего случая имеем
| классы |  |  |  | ||||||||||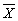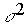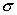
| Экспериментальный контрольный | 19 Это означает, что в одном классе пос е щаемость высокая, стабильная, а 1 д ругом — отличается непостоянством.
11.3. СОДЕРЖАТЕЛЬНЫЙ АНАЛИЗ ДАННЫХ И ПОЛУЧЕНИЕ ВЫВОДОВОбщий алгоритм содержательного анализа данных эксперимента был приведен в г л. VI. Осн о вными задач а ми ан а лиза являются сравнение получ ен ных данных по тем схемам, которые были заложе н ы в логику ис сл е д ова н ия, установление сп р аведливости гип о тез, определение сте п ени достижения целей и задач экс п ерим ента. 11.4. ДОСТОВЕРНОСТЬ РЕЗУЛЬТ А ТОВКак уже отмеча л ось, основным свойством педагогических пр оцессов, явлений является их вероятностный характер (при данных условиях они могут произойти, реализоваться, но м о гут и не про изойти). Для так и х явле н ий существ е нную роль играет понятие вероятности. Если в экспер и менте по л учен ка к ой-то к ол и чественный результат (X), то возникает вопрос: какова вероятность того, что этот р ез ульт а т будет получен в повторном эксперименте при тех же условиях .
В этой формуле заключается статистический смысл принци п а воспроизводимости педагогического эксперимента: если повторить (или дублировать) эксперимент, то его результат будет с определенной вероятностью находиться в пределах доверительного интервала Таблица 1. Коэффицие н т Стьюдента
Для определения доверительного интервала по методу Стьюдента-Госсета: Результат экспериментальной сер ии n изменений в методике Стьюдента выражается так Пример. Рассчитать результат (средней балл и доверительный интервал) срезовой контрольной работы в экспериментальном классе. Всего учащихся — 30 человек, из них получили оценки: “5” — 6 человек; “4” — 10; “3” — 12; “2” — 2 человека. б) Сред н яя квадратичная ошибка среднего
в— г) Задаемся 95 % . достоверностью и по таблице 1 находим
д) Вычисляем до в ерител ь ный интервал;
Результат контрольной работы Значит, результат аналогичной повторной контрольной работы в этом классе будет с 95 % вероятностью лежать в этой области (от 3,5 балла до 3,9 балла). Достоверность сравнения. Средние значения параметров педагогического проце с са, полученные в результате срезовых измерений в различн ы х группах (экспериментальной и контрольной) м о гут быть бл из к и ми, но никогда не бывают одинаковым и (
е) вычисляется разность
то разница между показателя м и должна считаться существенной с достоверностью Р == 0,9. то должно считаться существенным сходство между результатами обеих групп.
При этом экспериментатор должен помнить, что cущecтвoвание значимой разницы или сходства количественных показателей без поддержки другими аргументами нельзя брать в основу выводов (особенно в сомнительных случаях). Р ек о мендуемая литер а тура Аванесов В. С. Применение статистич е ских методов и ЭВМ в педагоги ческих исследованиях. // Введ е ние в научное исследование по педагогике. / Под. р ед. В. И. Журавылева. М., 1988*. Дополнительная л и т ератураАрханг е льский С. И. Лекции по научной организации учебного процесса в высшей школе. М ., 1976, с. 148-168. Источник |
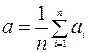
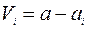
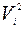
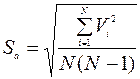
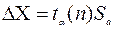
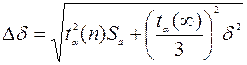
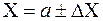
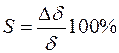
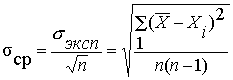
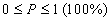
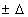ХДОВ), то можно говорить об определенной вероятности того, что результат повторного эксперимента будет находиться в пределах этой области. 
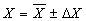ДОВ (с достоверностью=Р ) (5)
. 
; 
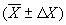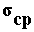
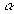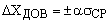(с достоверностью=Р)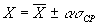
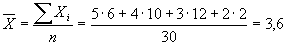
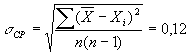
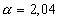
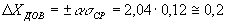
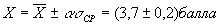
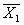и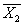 
). Вывод же о справедливости гипотезы может быть сделан на осно в ани и заключения либо о различии, либо о сходстве результатов. 
; 
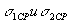