Различные способы обоснования истинности предложений в начальном обучении математике
Страницы работы
Содержание работы
В. Н. МЕДВЕДСКАЯ.Различные способы обоснования истинности предложений в начальном обучении математике//Начальная школа, 1983. — №2. – С.26-31.
Развивающее обучение предполагает систематическое и целенаправленное руководство, интеллектуальным ростом учащихся и вооружение их в процессе учения приемами и методами познавательной деятельности. Одним из средств решения поставленных задач являются доказательства.
Впервые с математическим доказательством учащиеся встречаются в курсе геометрии VI класса. Сложность мыслительной деятельности по доказыванию требует заблаговременной, длительной подготовки. Пропедевтическая работа в этом направлении может быть начата в курсе математики начальной школы. Объяснительная записка к программе этого курса ориентирует учителей на необходимость полного использования всех заложенных в нем предпосылок для формирования у детей таких приемов умственной деятельности, как сравнение, моделирование, получение выводов доказательства включаются в систему методов путем наблюдений и логических рассуждений
Для планомерного управления формированием доказывающего мышления у младших школьников учителю необходимо иметь четкие представления о сущности доказательства, о возможностях его применения в начальном обучении математике, о значении такой работы в целях подготовки учащихся к изучению математики в средней школе.
Под доказательством в логике понимают логическую операцию по обоснованию истинности одного суждения с помощью других истинных суждений. Поэтому традиционным является деление доказательства на три структурные части: 1) доказываемое суждение (тезис); 2) основание доказательства (достоверные суждения, из которых следует тезис); 3) способ доказательства (демонстрация).
В математических доказательствах основаниями для тезиса могут быть только определения, аксиомы или ранее доказанные теоремы. Основной способ таких доказательств — дедуктивный вывод. В начальной же математике, как известно, нет ни аксиом, ни теорем, да и определений немного. Значит, основания для установления истинности высказываемых суждений здесь должны быть иными.
Отбор таких оснований определяется особенностями восприятия младших школьников, уровнем их знаний, а также степенью сформированности тех или иных мыслительных операций Наглядный, конкретный характер мышления детей 7—10 лет, ограниченность их знаний ориентируют на использование в качестве критериев истины опыта, наблюдений, измерений, практики. По мере увеличения объема знаний основаниями доказательства могут служить результаты вычислений, ранее выведенные правила, свойства арифметических действий.
Анализ учебников математики для I— III классов, соответствующей им методической литературы и наблюдения уроков позволяют выделить следующие способы o6основания истинности предложений, используемых в начальном обучении математике: эксперимент, неполный индуктивный вывод, измерение, умозаключение по аналогии, дедуктивный вывод, вычисление. Назовем их способами предматематического доказательства. Приставка пред указывает на отличие такого доказательства от математического и на его роль в предварительной, предшествующей подготовке младших школьников к проведению строгих логических доказательств. Все названные способы предматематического доказательства приемов, позволяющих полнее реализовать заложенные в программе возможности интеллектуального развития учащихся. Рассмотрим каждый из них в отдельности.
1. Эксперимент — самый распространенный в начальной математике способ получения новых знаний, истинность которых устанавливается путем сопоставления их с действительностью, с результатами непосредственного чувствительного восприятия.
Экспериментально[1] доказываются предложения вида 2 1 2 3 4
Источник
Способы обоснования истинности суждений
3.7. Способы обоснования истинности суждений
Непременным условием развивающего обучения является формирование у учащихся способности обосновывать (доказывать) те суждения, которые они высказывают. В практике эту способность обычно связывают с умением рассуждать, доказывать свою точку зрения.
Суждения бывают единичными: в них что–то утверждается или отрицается относительно одного предмета. Например: «Число 12 –четное; квадрат АВСD не имеет острых углов; уравнение 23–х = 30 не имеет решения (в рамках начальных классов) и т. д.».
Помимо единичных суждений различают суждения частные и общие. В частных что–то утверждается или отрицается относительно некоторой совокупности предметов из данного класса или относительно некоторого подмножества данного множества предметов. Например: «Уравнение х – 7 = 10 решается на основе взаимосвязи между уменьшаемым, вычитаемым и разностью». В этом суждении речь идет об уравнении частного вида, представляющего собой подмножество множества всех уравнений, изучаемых в начальных классах.
В общих суждениях что–то утверждается или отрицается относительно всех предметов данной совокупности. Например:
«В прямоугольнике противоположные стороны равны». Здесь речь идет о любом, т.е. о всех прямоугольниках. Поэтому суждение является общим, хотя в данном предложении слово «всех» отсутствует. Любое уравнение в начальных классах решается на основе взаимосвязи между результатами и компонентами арифметических действий. Это также общее суждение, так как охватывает всевозможные уравнения, встречающиеся в курсе математики начальных классов.
Предложения, выражающие суждения, могут быть различными по форме: утвердительными, отрицательными, условными (например: «если число оканчивается нулем, то оно делится на 10»).
Как известно, в математике все предложения, за исключением исходных, как правило, доказываются дедуктивно. Суть дедуктивных рассуждений сводится к тому, что на основе некоторого общего суждения о предметах данного класса и некоторого единичного суждения о данном объекте высказывается новое единичное суждение о том же объекте. Общее суждение принято называть общей посылкой, первое единичное суждение – частной посылкой, новое единичное суждение – заключением. Пусть, например, требуется решить уравнение: 7*x=14. Для нахождения неизвестного множителя используется правило: «Если значение произведения разделить на один множитель (известный), то получим другой (значение неизвестного множителя)».
Это правило (общее суждение) – общая посылка. В данном уравнении произведение равно 14, известный множитель 7. Это частная посылка.
Заключение: «нужно 14 разделить на 7, получим 2». Особенность дедуктивных рассуждений в начальных классах заключается в том, что они применяются в неявном виде, т. е. общая и частные посылки в большинстве случаев опускаются (не проговариваются), ученики сразу приступают к действию, которое соответствует заключению.
Поэтому, собственно, и создается впечатление, что дедуктивные рассуждения отсутствуют в курсе математики начальных классов.
Для сознательного выполнения дедуктивных умозаключений необходима большая подготовительная работа, направленная на усвоение вывода, закономерности, свойства в общем виде, связанная с развитием математической речи учащихся. Например, довольно длительная работа по усвоению принципа построения натурального ряда чисел позволяет учащимся овладеть правилом:
«Если к любому числу прибавить 1, то получим следующее за ним число; если из любого числа вычтем 1, то получим предшествующее ему число».
Составляя таблицы П+1 и П – 1, ученик фактически пользуется этим правилом как общей посылкой, выполняя тем самым дедуктивные рассуждения. Примером дедуктивных умозаключений в начальном обучении математике является и такое рассуждение:
«4 или =, чтобы получилась верная запись:
учащиеся предпочитают заменять рассуждения вычислениями:
125–87 . 127–87 246–93 . 249–93 584–121. 588– 121
4. Сравни выражения и поставь знаки или = :
304:8 . 3044 243:9 . 243:3 1088:4 . . 1088:2
5. Как быстро найти сумму в каждом столбике:
9999 12 15 12 16 30 30 32 32 40 40 40 40 Ответ: 91.
Таким образом, дедуктивные рассуждения могут являться одним из способов обоснования истинности суждений в начальном Курсе математики. Учитывая, что они доступны не всем младшим школьникам, в начальных классах используются и другие способы обоснования истинности суждений, которые в строгом смысле нельзя отнести к доказательствам. К ним относятся эксперимент, вычисления и измерения.
Эксперимент обычно связан с применением наглядности и предметных действий. Например, ребенок может обосновать суждение 7 > 6, выложив в одном ряду 7 кругов, под ним – 6. Установив между кругами первого и второго ряда взаимно–однозначное соответствие, он фактически обосновывает свое суждение (в первом ряду один круг без пары, «лишний», значит, 7>6). Ребенок может обращаться к предметным действиям и для обоснования истинности полученного результата при сложении, вычитании, умножении и делении, при ответе на вопросы: «На сколько одно число больше (меньше) другого?», «Во сколько раз одно число больше (меньше) другого?». Предметные действия могут быть заменены графическими рисунками и чертежами. Например, для обоснования результата деления 7:3=2 (ост.1) он может использовать рисунок:
Для формирования у учащихся умения обосновывать свои суждения полезно предлагать им задания на выбор способа действия (при этом оба способа могут быть: а) верными, б) неверными, в) один верным, другой неверным). В этом случае каждый предложенный способ выполнения задания можно рассматривать как суждение, для обоснования которого учащиеся должны использовать различные способы доказательств.
Например, при изучении темы «Единицы площади» учащимся предлагается задание (М2И):
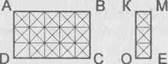
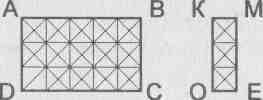
Во сколько раз площадь прямоугольника АВСD больше прямоугольника КМЕО? Запиши ответ числовым равенством.
Маша записала такие равенства: 15:3=5, 30:6=5.
Миша – такое равенство: 60:12=5.
Кто из них прав? Как рассуждали Миша и Маша?
Для обоснования суждений, высказанных Мишей и Машей, учащиеся могут использовать как способ дедуктивных рассуждений, где в качестве общей посылки выступает правило кратного сравнения чисел, так и практический. В этом случае они опираются на приведенный рисунок.
Предлагая способ решения задачи, учащиеся также высказывают суждения, используя для их доказательства математическое содержание, данное в сюжете задачи. Прием выбора готовых суждений активизирует эту деятельность. В качестве примера можно привести такие задания:
Туристы в первый день прошли 18 км, во второй день, двигаясь с той же скоростью, они прошли 27 км. С какой скоростью шли туристы, если они затратили на весь путь 9 ч?
Миша записал решение задачи так:
3) 2+3=5 (км/ч) Маша – так:
2) 45:9=5 (км/ч) Кто из них прав: Миша или Маша?
Сколько картофелин собрали с 10 кустов, если с трех собрали по 7 картофелин, с четырех по 9, с шести по 8, а с семи по 4 картофелины? Маша решила задачу так:
3) 21+28=49 (к.) Ответ: 49 картофелин собрали с 10 кустов. А Миша так решил задачу:
3) 36+48=84 (к.) Ответ: 84 картофелины собрали с 10 кустов. Кто из них прав?
Процесс выполнения любого задания должен всегда представлять цепочку суждений (общих, частных, единичных), для обоснования истинности которых учащиеся используют различные способы.
Покажем это на примере заданий:
V Вставь числа в «окошки», чтобы получились верные равенства:
П : 6 = 27054 П:7= 4083 (ост. 4)
Учащиеся высказывают общее суждение: «если значение частного умножим на делитель, то получим делимое». Частное суждение: «значение частного – 27054, делитель – б». Заключение:
Теперь в качестве общей посылки выступает алгоритм письменного умножения, находится результат: 162324. Высказывается суждение: 162324:6=27054.
Истинность этого суждения можно проверить, выполнив деление «уголком» или воспользовавшись калькулятором.
Аналогично поступают со второй записью.
Составь верные равенства, используя числа: 6, 7, 8, 48, 56.
Учащиеся высказывают суждение:
6*8=48 (обоснование – вычисления) 56 – 48=8 (обоснование – вычисления)
8*6=48 (для обоснования суждения можно воспользоваться общей посылкой: «от перестановки множителей значение произведения не изменится»).
48:8=6 (тоже возможна общая посылка и т.д.)’ Таким образом, в большинстве случаев для обоснования истинности суждений в начальном курсе математики учащиеся обращаются к вычислениям и дедуктивным рассуждениям. Так, обосновывая результат при решении примера на порядок действия, они пользуются общей посылкой в виде правила порядка действий, затем выполняют вычисления.
Измерение как способ обоснования истинности суждений обычно применяется при изучении величин и геометрического материала. Например, суждения: «синий отрезок длиннее красного», «стороны четырехугольника равны», «одна сторона прямоугольника больше другой» дети могут обосновать измерением.
• Задание 93. Опишите способы обоснований истинности суждений. высказанных учащимися при выполнении следующих заданий. При изучении каких вопросов курса математики начальных классов целесообразно предложить эти задания 9
Можно ли, не выполняя вычислений, утверждать, что значения выражений в каждом столбике одинаковы:
9*7+9+5 8*6+8+3 7*9+9+5 8*7+3 9*8+5 7*8+3
Можно ли утверждать, что значения выражений в каждом столбике ‘одинаковы:
12*5 16*4 (8+4)*5 (8+8)*4 (7+5)*5 (9+7)*4 (10+2)*5 (10+6)*4
Вставь знаки или =, чтобы получились верные записи:
(14+8)*3 . 14*3+8*3 (27+8)*6 . 27*6+8 (36+4)*18 . 40*18 .
Какие знаки действий нужно вставить в «окошки», чтобы получить верные равенства
8*8=8П7П8 8*3=8П4П8 8*6=6П8П0 8*5=8П0П32
Можно ли утверждать, что значения выражений в каждом столбике одинаковы:
8*(4*6) (9*3)*3 8*24 2*27 (8*4)*6 9*(3*2) 6*32 (2*3)*9
Источник
Способы доказательств, используемые в математике.
В начальном курсе математики большинство предположений доказываются дедуктивно.
Пусть, например, требуется решить уравнение: 7 
x=14. Для нахождения неизвестного множителя используется правило: «Если значение произведения разделить на один множитель (известный), то получим другой (значение неизвестного множителя)».
Это правило (общее суждение) – общая посылка. В данном уравнении произведение равно 14, известный множитель 7. Это частная посылка.
Заключение: «нужно 14 разделить на 7, получим 2».
Особенность дедуктивных рассуждений в начальных классах заключается в том, что они применяются в неявном виде, т. е. общая и частные посылки в большинстве случаев опускаются (не проговариваются), ученики сразу приступают к действию, которое соответствует заключению.
Для сознательного выполнения дедуктивных умозаключений необходима большая подготовительная работа, направленная на усвоение вывода, закономерности, свойства в общем виде, связанная с развитием математической речи учащихся. Например, довольно длительная работа по усвоению принципа построения натурального ряда чисел позволяет учащимся овладеть правилом:
«Если к любому числу прибавить 1, то получим следующее за ним число; если из любого числа вычтем 1, то получим предшествующее ему число».
Составляя таблицы 
+1 и – 1, ученик фактически пользуется этим правилом как общей посылкой, выполняя тем самым дедуктивные рассуждения. Примером дедуктивных умозаключений в начальном обучении математике является и такое рассуждение:
«4 6, выложив в одном ряду 7 кругов, под ним – 6. Установив между кругами первого и второго ряда взаимно–однозначное соответствие, он фактически обосновывает свое суждение (в первом ряду один круг без пары, «лишний», значит, 7>6). Ребенок может обращаться к предметным действиям и для обоснования истинности полученного результата при сложении, вычитании, умножении и делении, при ответе на вопросы: «На сколько одно число больше (меньше) другого?», «Во сколько раз одно число больше (меньше) другого?». Предметные действия могут быть заменены графическими рисунками и чертежами. Например, для обоснования результата деления 7:3=2 (ост.1) он может использовать рисунок:
Для формирования у учащихся умения обосновывать свои суждения полезно предлагать им задания на выбор способа действия (при этом оба способа могут быть: а) верными, б) неверными, в) один верным, другой неверным). В этом случае каждый предложенный способ выполнения задания можно рассматривать как суждение, для обоснования которого учащиеся должны использовать различные способы доказательств.
Например, при изучении темы «Единицы площади» учащимся предлагается задание :
Во сколько раз площадь прямоугольника АВСD больше прямоугольника КМЕО? Запиши ответ числовым равенством.
Маша записала такие равенства: 15:3=5, 30:6=5.
Миша – такое равенство: 60:12=5.
Кто из них прав? Как рассуждали Миша и Маша?
Для обоснования суждений, высказанных Мишей и Машей, учащиеся могут использовать как способ дедуктивных рассуждений, где в качестве общей посылки выступает правило кратного сравнения чисел, так и практический. В этом случае они опираются на приведенный рисунок.
Предлагая способ решения задачи, учащиеся также высказывают суждения, используя для их доказательства математическое содержание, данное в сюжете задачи. Прием выбора готовых суждений активизирует эту деятельность. В качестве примера можно привести такие задания:
Туристы в первый день прошли 18 км, во второй день, двигаясь с той же скоростью, они прошли 27 км. С какой скоростью шли туристы, если они затратили на весь путь 9 ч?
Миша записал решение задачи так:
3) 2+3=5 (км/ч) Маша – так:
2) 45:9=5 (км/ч) Кто из них прав: Миша или Маша?
Сколько картофелин собрали с 10 кустов, если с трех собрали по 7 картофелин, с четырех по 9, с шести по 8, а с семи по 4 картофелины? Маша решила задачу так:
1)7 3=21 (к.)
2) 4 7=28 (к.)
Ответ: 49 картофелин собрали с 10 кустов.
А Миша так решил задачу:
2) 8 6=48 (к.)
Ответ: 84 картофелины собрали с 10 кустов. Кто из них прав?
№ 3. Вставь числа в «окошки», чтобы получились верные равенства:
[ ]: 6 = 27; [ ]:7= 40 (ост. 4)
Учащиеся высказывают общее суждение: «если значение частного умножим на делитель, то получим делимое». Частное суждение: «значение частного – 27, делитель – 6». Заключение: «27 6».
Теперь в качестве общей посылки выступает алгоритм устного умножения, находится результат:162.Высказывается суждение: 162:6=162.
Истинность этого суждения можно проверить, выполнив деление.
Аналогично поступают со второй записью.
Составь верные равенства, используя числа: 6, 7, 8, 48, 56.
Учащиеся высказывают суждение:
6 8=48 (обоснование – вычисления) 56 — 48=8 (обоснование – вычисления)
8 6=48 (для обоснования суждения можно воспользоваться общей посылкой: «от перестановки множителей значение произведения не изменится»).
48:8=6 (тоже возможна общая посылка и т.д.).
Таким образом, в большинстве случаев для обоснования истинности суждений в начальном курсе математики учащиеся обращаются к вычислениям и дедуктивным рассуждениям. Так, обосновывая результат при решении примера на порядок действия, они пользуются общей посылкой в виде правила порядка действий, затем выполняют вычисления.
Измерениекак способ обоснования истинности суждений обычно применяется при изучении величин и геометрического материала.
Например, суждения: «синий отрезок длиннее красного», «стороны квадрата равны», «одна сторона прямоугольника больше другой» дети могут обосновать измерением.
Источник
