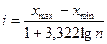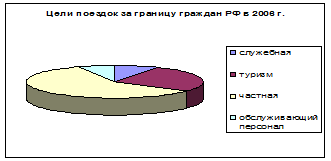Способы обобщения статистических данных

§ 5. СТАТИСТИЧЕСКИЕ ОБОБЩЕНИЯ

§ 5. СТАТИСТИЧЕСКИЕ ОБОБЩЕНИЯ

Особым видом умозаключений неполной индукции являются статистические обобщения, связанные с анализом массовых событий. К ним относятся, например, массовые транспортные перевозки пассажиров и грузов, рождаемость и смертность людей, распространение заболеваний, транспортные происшествия, динамика преступлений и многие другие.

Учитывая трудности выявления причинных зависимостей, анализ таких массовых событий позволяет установить устойчивое распределение интересующих исследователя случайных признаков. Количественная информация, выражающая устойчивые тенденции развития, имеет важное практическое значение для правильной организации обслуживания населения, профилактических мероприятий, борьбы с преступностью и т. п. Анализ массовых событий ведется чаще всего путем не сплошного, а выборочного исследования отдельных групп или образцов и логического переноса полученных результатов на все их множество. Вывод в этом случае протекает в форме статистического обобщения.

Статистическое обобщение — это умозаключение неполной индукции, в котором установленная в посылках количественная информация о частоте определенного признака в исследуемой группе (образце) переносится в заключении на все множество явлений этого рода.

В отличие от индукции через перечисление при отсутствии противоречащего случая в посылках статистического умозаключения фиксируется следующая информация: (1) общее число составляющих исследуемую группу, или образец случаев; (2) число случаев в которых присутствует интересующий исследователя признак; (3) частота проявления интересующего признака.

Для построения схемы статистического обобщения введем условные обозначения: S — исследуемый образец; р — интересующий исследователя признак; m — общее число наблюдаемых случаев (элементов образца); n — число благоприятных случаев, когда явление обладает признаком р; f(р) — частота признака р; К — популяция, или множество явлений, на которое распространяется частота признака.

Частота появления признака р в образце S представляет собой отношение числа благоприятных случаев n к общему числу исследованных явлений m:

f(p) = n/m.

Например, статистическая информация о совершении такого рода преступлений, как хулиганство, показывает, что 95 из 100 случаев хулиганских действий совершаются в состоянии алкогольного опьянения. Значит, частота хулиганства, связанная с алкогольным опьянением, определяется как 95/100, т. е. равна 95%.

Частота появления признака в статистических описаниях принимает числовое значение в интервале между 0 и 1: 0 n, тем самым f(p) всегда будет меньше единицы, но больше нуля.

В том случае, когда f(p) = 0, это значит, что среди наблюдаемых не обнаружено ни одного явления, обладающего этим признаком. На этой основе может быть построено обычное индуктивное обобщение с отрицательным заключением: поскольку ни одно S не обладает свойством р, значит, можно заключить, что весь класс К не обладает этим свойством. Точно так же и в случае f(p) = 1 можно построить обычную индуктивную генерализацию с утвердительным заключением. Поскольку число случаев появления признака (n) равно числу всех исследованных (m), т. е. n = m, значит, каждое S обладает р. Отсюда заключают, что весь класс К обладает этим признаком.

Схема статистического обобщения:

Вероятно, К имеет f(p).

Это означает: признак р появляется в образце S с частотой f; образец S является подмножеством популяции К, которая по числу элементов больше S; отсюда следует, что признак р будет встречаться в популяции К с частотой f.

Статистическое обобщение, являясь выводом неполной индукции, относится к недемонстративным умозаключениям. Логический переход от посылок к заключению дает лишь проблематичное знание. Степень обоснованности статистического обобщения зависит от специфики исследованного образца: его величины по отношению к популяции и представительности (репрезентативности). Если образец по объему приближается к популяции, тем основательнее обобщение, поскольку возможность ошибки становится минимальной. Репрезентативность образца означает меру его представительности: насколько разнообразие элементов в образце отражает их разнообразие в популяции.

Тщательность статистического описания исследуемого образца и логически корректный перенос частоты признака на популяцию обеспечивают высокую вероятность и тем самым практическую эффективность статистических обобщений в различных областях науки, культуры, производства, правовой деятельности.

Вопросы для самопроверки

1. Что такое статистические обобщения?

2. Какова структура статистических обобщений и чем они отличаются от перечислительной индукции?

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

2.1. Понятие как результат обобщения

2.1. Понятие как результат обобщения Отображение внешнего мира человеком начинается с чувственного познания, когда предметы и явления предстают перед ним как объекты непосредственного, живого созерцания. На этой ступени важная роль принадлежит органам чувств, с помощью

5.6. Статистические умозаключения

5.6. Статистические умозаключения С расширением применения статистических методов в естественных, технических, а в последние десятилетия и социальных науках ученые и практики все чаще стали прибегать в своей аргументации к статистическим обобщениям и выводам. Подобные

XIX век – время обобщения теоретических исканий эпохи «царства разума»

XIX век – время обобщения теоретических исканий эпохи «царства разума» Социально-политические процессы периода XIX века знаменательны не только для истории Европы, но и для всего мира. Созрела глобальная цивилизация, когда европейцы, европейская культура оказывали свое

К. МАРКС СТАТИСТИЧЕСКИЕ ДАННЫЕ О ЖЕЛЕЗНЫХ ДОРОГАХ

К. МАРКС СТАТИСТИЧЕСКИЕ ДАННЫЕ О ЖЕЛЕЗНЫХ ДОРОГАХ Английские железные дороги имеют ровесников среди людей, им 30 лет. За исключением национального долга, ни одна другая отрасль национальной экономики не достигала такого гигантского развития за столь короткий срок. По

§ 7. Роль обобщения в математике

§ 7. Роль обобщения в математике В предыдущей главе мы обратили внимание на изменение в значении слов в процессе обобщения. В математике подобный процесс также имеет место и чаще всего связан с тем, что называется «современным обобщением числа». Несложно впасть в ошибку

Глава XVI. Статистические методы

Глава XVI. Статистические методы § 1. Потребность в статистических методах В предыдущей главе мы обсуждали пересчет и измерение как способы уточнения наших идей о предметах. Однако в результате этих двух процессов производятся большие совокупности численных данных, и

Глава XVI. Статистические методы

Глава XVI. Статистические методы 1. Исследование уровня смертности в городских и сельских местностях в США с 1901 по 1911 г. показывало, что уровень смертности в городах был выше, чем уровень смертности в селах.a. Означает ли это, что города были менее пригодными местами для

26. Ограничены ли обобщения рамками исторических периодов?

26. Ограничены ли обобщения рамками исторических периодов? Тот факт, что проблема социальных экспериментов была рассмотрена нами прежде сколько-нибудь подробного обсуждения социологических законов, из теорий, гипотез или «обобщений», вовсе не означает что наблюдения и

Приблизительные обобщения

Приблизительные обобщения Приблизительное обобщение выглядит так: Большинство S суть P Например, «большая часть хипстеров креативна».Приблизительные обобщения употребляются, например, в медицине. Когда мы говорим, что «для большинства людей 800 грамм этанола —

Fallacia fictae universalitatis (Иллюзия обобщения)

Fallacia fictae universalitatis (Иллюзия обобщения) Эта ошибка индукции — поспешное обобщение — встречается чаще всего. «Все полицейские берут взятки». «Все евреи расчётливы». «Все негры имеют длинный член». «Все православные —

Источник

Модуль 2. Обобщение статистических данных

Блок 3. Статистическая информация и статистические показатели

Статистическая информация – это первичный статистический материал, формирующийся в ходе статистического наблюдения, который затем систематизируется, сводится, обрабатывается, анализируется и обобщается.

Важными условиями качественного использования статистической информации являются ее: массовость, систематичность получения и обработки, а также возможность длительного ее хранения на различных носителях. Статистическая информация может быть подразделена по:

— принадлежности к отраслям экономики;

Статистический показатель представляют собой обобщенную количественную характеристику явлений и процессов в тесной увязке с их особенностями в конкретных условиях места и времени. Показатели имеют количественную и качественную стороны. Количественная сторона определяет конкретный размер показателя, его величину, а качественная сторона показателя отражает его содержательную часть. Совокупность показателей, всесторонне отражающих развитие явления, образуют систему показателей.

Социально-экономические индикативные показатели выступают в роли индикаторов, характеризующих состояние развития экономики в целом, отдельных отраслей. Такие показатели дают представление об уровне развития страны в динамике по сравнению с другими странами, отдельных регионов в рамках одной страны. Эти показатели являются основой для построения прогнозов развития по различным отраслям экономики, к ним относятся:

— валовой внутренний продукт (ВВП);

— объем экспорта и импорта;

— среднегодовая численность занятых и безработных;

— среднемесячная начисленная заработная плата;

— денежные доходы и расходы населения;

— средний уровень образования.

Индикативными показателями могут выступать и интегральные показатели, которые выражают уровень социально-экономического развития отдельных регионов и страны в целом. Существуют и применяются различные системы оценки уровня жизни населения. Например, рабочая группа по социальной статистике ООН предлагала в качестве таких показателей национальный доход на душу населения, долю расходов на питание в общих расходах домохозяйств, относительный коэффициент смертности и т.д. Единого, универсального показателя пока не выработано.

Блок 4. Статистическая сводка, группировки, классификации, статистические таблицы, графики

Информация полученная в ходе статистического наблюдения требует обобщения и систематизации, для этого осуществляется статистическая сводка, когда индивидуальные данные превращаются в упорядоченную систему показателей, которые дают возможность оценить состояние явления и установить тенденции и закономерности его развития.

Статистическая сводка позволяет перейти от единичных значений изучаемой совокупности к обобщающим показателям, характеризующим уже всю совокупность в целом. Сводка предусматривает систематизацию и группировку данных, характеристику групп системой показателей и представление сводной информации в виде таблиц и графиков.

Статистическая сводка проходит следующие этапы:

1. Формулировка задачи на основе целей исследования;

2. Образование групп и подгрупп, определение группировочных признаков, числа групп, интервалов групп, комбинированных группировок;

3. Техническая сторона сводки: проверка полноты и качества информации, подсчет итогов и расчеты показателей, характеризующих совокупность в целом и отдельных ее частей.

Сводка может осуществляться централизованно и децентрализовано.

Централизованная сводка предполагает сосредоточение данных в одном месте и обработка их по единой методике;

Децентрализованная сводка осуществляется поэтапно снизу до верху по иерархической лестнице управления.

Группировка– процедура объединения в группы однородных по какому-либо признаку объектов и характеристика образованных групп системой показателей. Статистическая группировка призвана в общей совокупности определить однородные группы, отличающиеся друг от друга в количественном или качественном отношении и выделить действующие в них социально-экономические типы.

Группировки призваны решать три основные задачи:

1. Изучение структуры изучаемой совокупности;

2. Выделение в общей совокупности действующих основных типов и изучение их взаимодействия между собой;

3. Выявление взаимосвязи между признаками.

Выделяют следующие основные виды группировок: типологические, структурные, аналитические и комбинированные.

Типологические группировки предполагают выделение из множества признаков основных, качественно однородных типов явлений, которые позволяют проследить во времени их зарождение, развитие и отмирание.

Группировка по одному признаку называется простой; если производится группировка по двум и более признакам, где каждая группа разбивается на последующие подгруппы, то такая группировка – комбинационная.

Признаки могут быть атрибутивными (качественными) и количественными. При разработке атрибутивных признаков число групп определяется свойствами изучаемого явления.

При группировке количественных значений признака выделение типов состоит в определении величины групп, границы которых устанавливают новое качество изучаемого явления.

Структурные группировкипозволяют изучать выделенные типы с точки зрения их структуры и состава. Структурные группировки используются для изучения строения исследуемого явления.

Аналитические группировки предназначены для изучения явления с точки зрения взаимосвязей между отдельными его признаками (факторными и результативными).

Комбинированные группировки предполагают использование нескольких группировок в определенном сочетании. Группировочные признаки в комбинированных группировках располагаются, начиная с атрибутивных признаков, в соответствии с логикой и последовательностью задачи изучения явления.

Число групп в группировках зависит от целей исследования и объема наблюдений.

Интервалы групп могут быть равными и неравными. Расчет величины интервала i при равных интервалах производится по формуле:

,

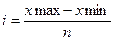
где х max, x min – максимальное и минимальные значения варьирующего признака, n – число групп.

Расчет величины интервала будет более формальным, если воспользоваться формулой Г. Стерджесса:

Для осуществления группировки из множества признаков явления необходимо выбрать определяющие, которые наиболее полно характеризуют изучаемое явление. Из многообразия признаков можно выделить и классифицировать:

— по форме выражения признаки могут быть атрибутивными, т. е. не выраженные количественно и количественные – признаки, принимающие различные количественные выражения. Количественные признаки могут быть дискретными (прерывными), выраженные только целыми числами и непрерывными, выраженными как целыми, так и дробными значениями;

— по характеру колеблемости признаки могут быть альтернативными, т. е. принимающими противоположные значения и признаками, имеющими множество количественных значений;

— по роли, которую играют признаки во взаимосвязи изучаемых явлений, они могут быть факторными, т.е. воздействующими на другие признаки и результативными – испытывающими на себе влияние других признаков. В зависимости от постановки задачи и от сложившейся ситуации факторные и результативные признаки могут поменяться местами.

Разновидностью группировок являются классификации; их необходимость обусловлена многообразием атрибутивных признаков, характеризующих явления и процессы и позволяющих относить их к определенным группам и классам. Статистические классификации представляют собой устойчивую номенклатуру классов и групп, сформированных на основе сходства и различия единиц исследуемого явления. При наличии нескольких признаков у отдельной единицы их относят к определенной группе по признаку, имеющему преобладающее значение.

Для унификации статистической информации в системе Росстата используется система классификаторов. Классификатор – это систематизированный свод классификационных признаков с их кодификацией. Классификаторы подразделяются на три группы:

Читайте также:  Способ промышленного получения кремния

— общегосударственные — применяются во всех отраслях и на всех уровнях управления;

— отраслевые – применяются в пределах одной отрасли;

— локальные – применяются на предприятиях (организациях) или группе предприятий.

В ходе реформирования российской статистики в 90-х годах был осуществлен переход от методологии баланса народного хозяйства к методологии системы национальных счетов (СНС). В соответствии с последней версией СНС-93 определение макроэкономических показателей предполагает использование системы общероссийских классификаторов, которые должны соответствовать международным стандартам ООН и Европейского союза (ЕС).

Был сформирован Единый государственный регистр предприятий и организаций, учреждений и объединений (ЕГРПО). Этот регистр позволяет группировать предприятия по:

— отраслям и видам деятельности;

— формам собственности и организационно-правовым формам;

— территориям и экономическим показателям.

ЕГРПО включает информацию о регистрационном коде субъекта; сведения об отраслевой, территориальной принадлежности, подчиненности, виду собственности, организационно-правовой форме; справочную информацию (Ф.И.О. руководителя, адрес и другие реквизиты); экономические сведения по производственной деятельности. Информационной основой ЕГРПО являются: Общероссийский классификатор предприятий и организаций (ОКПО), Общероссийский классификатор органов государственной власти и управления (ОКОГУ), Общегосударственный классификатор объектов организационно-правовых форм предприятий и организаций (ОКОПХ) и ряд других классификаторов. Всего в состав Единой системы классификации и кодирования технико-экономической и социальной информации входят 27 общероссийских классификаторов.

Статистические таблицы – наиболее рациональная форма представления результатов статистической сводки и обработки статистических материалов. По форме статистическая таблица представляет собой ряд пересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали – графы (столбцы, колонки). Составленная, но незаполненная таблица представляет собой макет таблицы.

По содержанию статистическая таблица имеет подлежащее и сказуемое. Подлежащее таблицы – это то, о чем говорится в таблице, представленное группами и подгруппами. Обычно подлежащее располагается в левой части таблицы.

Сказуемое таблицы – это то, что говорится о подлежащем. Это показатели, с помощью которых характеризуется изучаемое явление. Как правило, эти показатели размещают в правой части таблицы.

Оформленная таблица должна иметь общий заголовок, где изложено ее краткое содержание; единица измерения; названия строк и граф и итоги по ним.

Статистические таблицы подразделяются на: простые, групповые и комбинационные.

Простые таблицы в подлежащем содержат перечни, территориальные единицы, хронологические даты.

Групповые таблицы представляют статистические данные в сгруппированном виде, как правило, с выделением типов явления, что делает таблицу более информативной.

Комбинационные таблицы представляют собой комбинацию групп в сочетании с несколькими признаками изучаемого явления.

Подлежащие и сказуемое таблицы должны быть в тесной взаимосвязи с тем, чтобы можно было получить объективную и полную характеристику изучаемого явления.

Построение статистических таблиц предполагает соблюдение правил:

1. Таблицы должны быть наглядными и легко обозримыми;

2. Общий заголовок таблицы должен быть кратким с указанием единицы измерения, времени, территории, к которым относятся данные;

3. По строкам и графам, если это возможно, должны быть частные и общие итоги;

4. При заполнении таблиц необходимо использовать единые условные обозначения;

5. Показатели таблицы должны иметь одинаковую степень точности;

6. В таблицах значность цифр должна быть наименьшей.

Статистические графики –это наглядная, лаконичная и выразительная форма представления данных. График включает заголовок, где указывается, что представлено на графике, территория и время к которому относятся данные. Важные атрибуты графиков – условные единицы обозначения и масштаб.

По способу построения графики подразделяются на диаграммы и картодиаграммы. По графическому образу диаграммы могут быть:

— круговыми, треугольные, прямоугольные;

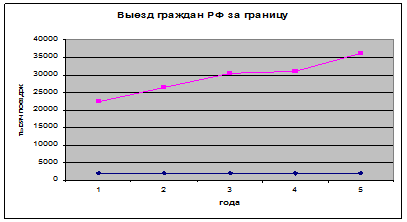
Линейные графики содержат значения показателей, соединенные отрезками прямых. Эти графики широко используются для анализа рядов распределения и временных рядов ( рис.1)

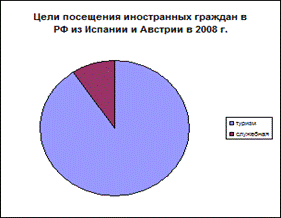
Секторные диаграммы применяются для представления структуры совокупности, где вся площадь круга принимается за 100%, а сектора представляют доли составляющих частей. Например, цели поездок граждан Российской Федерации за границу ( рис.2)

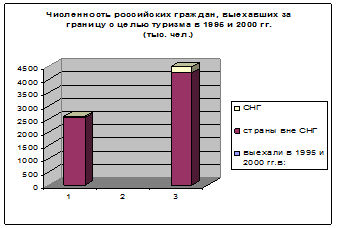
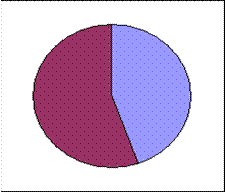
Круговые диаграммы представляют значения показателя в виде занимаемой им площади в общем объеме. Например, цели посещения иностранных граждан Российской Федерации в 2008 г. ( рис.3)

Испания	Австрия

Столбиковые диаграммы используются для представления значений состава показателей (рис.4)

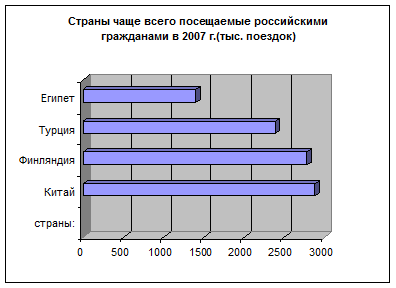
Ленточные диаграммы решают те же задачи, что и столбиковые, но графическое изображение показателей дается в горизонтальном виде ( рис. 5)

Фигурные диаграммы используются для изображения изменения показателя в динамике или для пространственных сравнений.

Картодиаграммы применяют для отображения пространственных данных. Например, на карту наносятся условные обозначения, отражающие наиболее часто посещаемые туристами регионы страны.

Источник