Приложение 3 (справочное). Формы выражения и способы установления пределов допускаемых погрешностей средств измерений
Формы выражения и способы установления пределов допускаемых погрешностей средств измерений
1. Формы выражения пределов допускаемых погрешностей
1.1. Пределы допускаемых погрешностей выражают в зависимости от характера изменения (в пределах диапазона изменений входного (выходного) сигнала) границ абсолютных погрешностей средств измерений конкретного вида, которые оценивают на основании принципа действия, свойств средств измерений, а также их назначения:
в форме приведенных погрешностей — если указанные границы можно полагать практически неизменными. Например пределы допускаемых погрешностей показывающих амперметров выражают в форме приведенных погрешностей, так как границы погрешностей средств измерений данного вида практически неизменны в пределах диапазона измерений;
в форме относительных погрешностей — если указанные границы нельзя полагать постоянными.
1.2. Пределы допускаемых погрешностей выражают в форме абсолютных погрешностей (т.е. в единицах измеряемой величины или в делениях шкалы средств измерений), если погрешность результатов измерений в данной области измерений принято выражать в единицах измеряемой величины или в делениях шкалы. Например пределы допускаемых погрешностей мер массы (длины) выражают в форме абсолютных погрешностей, так как погрешности результатов измерений массы (длины) принято выражать в единицах массы (длины).
2. Способы установления пределов допускаемых погрешностей
2.1. Пределы допускаемых погрешностей, выраженные в форме абсолютных (относительных) погрешностей, устанавливают одним из следующих способов в зависимости от характера изменения (в пределах диапазона измерений входного (выходного) сигнала) границ погрешностей средств измерений конкретного вида:
по формуле (1) настоящего стандарта — если границы абсолютных погрешностей можно полагать практически неизменными;
по формуле (4) настоящего стандарта — если границы относительных погрешностей можно полагать практически неизменными;
по формуле (2) или (5) настоящего стандарта — если границы абсолютных погрешностей можно полагать изменяющимися практически линейно;
в виде функции, графика или таблицы — если границы погрешностей необходимо принять изменяющимися нелинейно.
Откройте актуальную версию документа прямо сейчас или получите полный доступ к системе ГАРАНТ на 3 дня бесплатно!
Если вы являетесь пользователем интернет-версии системы ГАРАНТ, вы можете открыть этот документ прямо сейчас или запросить по Горячей линии в системе.
Источник
Нормирование погрешностей средств измерений Классы точности
Основные погрешности средств измерения нормируются путем задания пределов допускаемой основной погрешности, при которой средство измерения (СИ) по техническим требованиям может быть допущено к применению.
Для того чтобы оценить погрешность, которую внесет данное СИ в конечный результат, пользуются предельными значениями погрешности для данного типа СИ.
Предел допускаемой основной абсолютной погрешности D может быть представлен одним из трех способов:
— постоянным для любых значений X числом, характеризующим аддитивную погрешность,
— в виде двухчленной формулы, включающей аддитивную и мультипликативную погрешности,
— в виде уравнения
При сложной зависимости (6.3) допускается представлять погрешность в виде графика и таблицы.
Пределы допускаемой относительной погрешности для случая (6.1) в процентах выражают формулой
(6.4)
для случая (6.2) – формулой
где Хк – предел измерений;
— имеет смысл приведенной погрешности в конце диапазона измерений (при Х=Хк);
— имеет смысл приведенной погрешности в начале диапазона измерений (при Х = 0), причем c > d.
Предел допускаемой приведенной погрешности в процентах выражается формулой
(6.5)
где р – отвлеченное положительное число.
Согласно ГОСТ 8.401-80 для указания нормированных пределов допускаемых погрешностей значения р, q, с, d выражаются в процентах и выбираются из ряда чисел: (1;1,5;2;2,5;3;4;5 и 6) ´10n , где n=+1;0;-1;-2;-3 и т.д.
В настоящее время в эксплуатации большое число средств измерений, метрологические характеристики которых нормируются на основе классов точности.
Класс точности – обобщенная характеристика средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значение которых устанавливают в соответствующих стандартах.
Класс точности позволяет судить о том, в каких пределах находится погрешность средст измерений одного типа, но не характеризует точности измерений, выполняемых такими средствами, так как погрешность зависит и от метода измерений, и от условий измерений и т.д.
С использованием чисел указанного выше ряда чисел разработаны следующие условные обозначения классов точности СИ, наносимые на них.
1. Класс точности указывают просто одним из чисел приведенного выше предпочтительного ряда р (например, 1,5). Это используют для СИ, у которых предел допускаемой приведенной погрешности постоянен (присутствует только аддитивная погрешность), как в (6.1), Xn в (6.5) выражена в единицах измеряемой величины. Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой или степенной (с показателем степени не более двух) шкалой.
2. 
Класс точности указывает числом из приведенного выше ряда, под которым ставится треугольная скобка, например, . Такое обозначение применяют для приборов с резко неравномерной шкалой, для которых Хn выражают в единицах длины шкалы (мм, см, условных делениях). В этом случае при измерении, кроме значения измеряемой величины, обязательно должен быть записан отсчет X в единицах длины шкалы и предел Хn в этих же единицах, иначе нельзя будет вычислить погрешность результата. Таким способом обозначают класс точности омметров.
3. Число, обозначающее класс точности, обводят кружком например, . Такое обозначение применяют для СИ, у которых предел допускаемой относительной погрешности постоянен во всем диапазоне измерений (имеется только мультипликативная погрешность, (a в (6.2) равна нулю) и его определяют по (6.4). Таким способом нормируют погрешности измерительных мостов, магазинов, масштабных преобразователей. При этом обычно указывают границы рабочего диапазона, для которых справедлив данный класс точности.
4. Класс точности обозначается двумя числами, записываемыми через косую черту, т. е. в виде условной дроби c/d, например, 0,02 / 0,01. Такое обозначение применяют для СИ, у которых погрешность нормирована по двухчленной формуле (6.2). Таким способом указывают классы точности цифровых вольтметров, высокоточных потенциометров постоянного тока и других высокоточных приборов.
Источник
Способы нормирования предела допускаемой основной погрешности
Способ выражения предела допускаемой основной погрешности определяется назначением СИ и характером изменения погрешности в пределах диапазона измерения. В общем случае зависимость погрешности от входного сигнала может быть произвольной. Но из всего многообразия СИ по характеру изменения погрешности в пределах измерения можно выделить следующие основные группы:
СИ, для которых преобладает аддитивная составляющая погрешности;
СИ, для которых преобладает мультипликативная составляющая погрешности;
СИ, для которых необходимо учитывать обе (аддитивную и мультипликативную) составляющие погрешности.
В группе СИ, для которых преобладает аддитивная составляющая погрешности, предел допускаемой абсолютной погрешности можно записать выражением:
, где 
. (1.42)
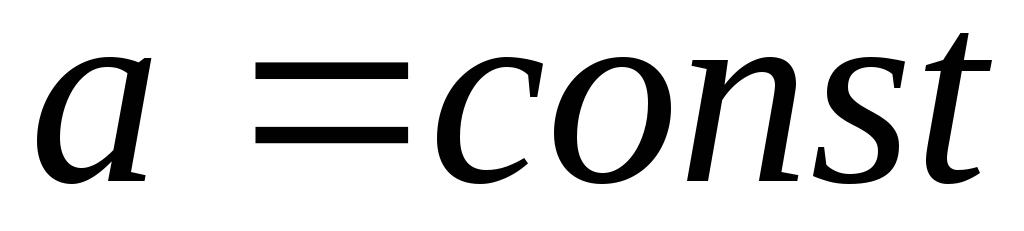
В ряде случаев оказывается удобно нормировать предел допускаемой абсолютной основной погрешности с использованием одного числового значения в соответствии с (1.42) (например, для средств измерения линейных размеров — микрометры, штангенциркули и т.п.). Класс точности в этом случае принято обозначать путем указания числа 
(как, например, для микрометра
) либо в виде условных обозначений, в качестве которых используются римские цифры или прописные буквы латинского алфавита. Причем классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны соответствовать меньшие цифры или буквы, находящиеся ближе к началу алфавита.
Но для электроизмерительных приборов нормировать предел допускаемой основной погрешности путем указания одного числового значения в соответствии с (1.42) оказалось не очень удобно, так как при этом трудно сравнивать приборы по точности, если они имеют разные диапазоны измерений или являются многопредельными. Для таких приборов более удобным оказалось нормировать предел допускаемой основной приведенной погрешности 
и выражать его в процентах:
, (1.43)
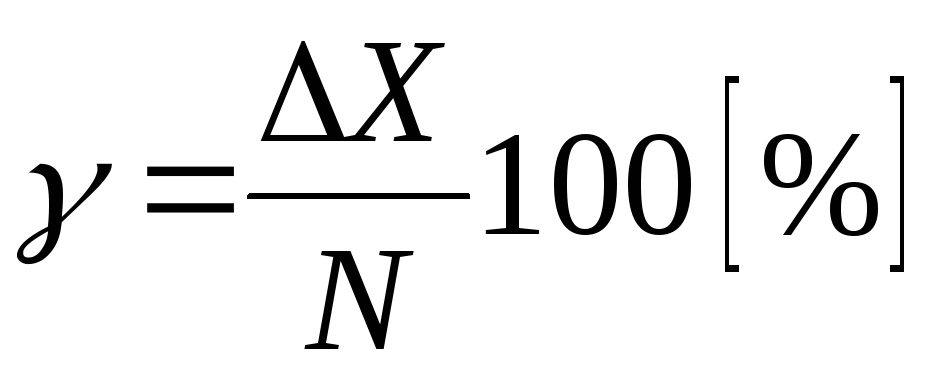
где N — нормирующее значение.
Нормирующее значение выбирается в зависимости от особенностей конкретного СИ. В соответствии с ГОСТ 8.401-80 нормирующее значение принимают равным:
конечному значению шкалы прибора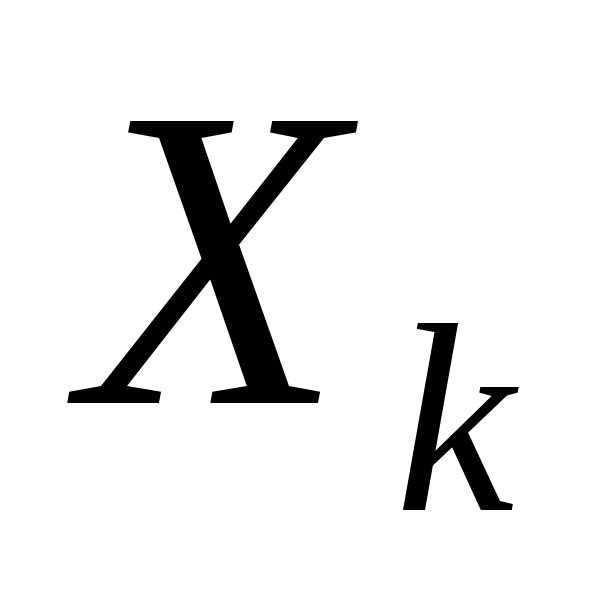 
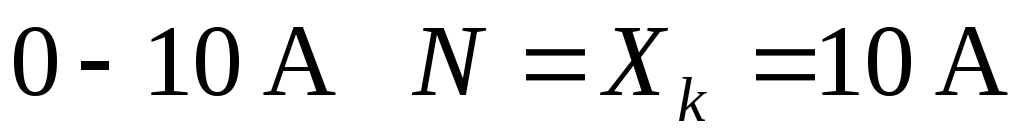
для СИ с равномерной шкалой, практически равномерной и степенной шкалой, если нулевая отметка находится на краю или вне шкалы (например, для амперметра со шкалой
);
сумме конечных значений шкалы прибора (без учета знаков), если нулевая отметка находится внутри шкалы (например, для миллиамперметра со шкалой 
);
номинальному значению измеряемой величины, если таковое установлено (например, для частотомера, предназначенного для контроля частоты питающей сети со шкалой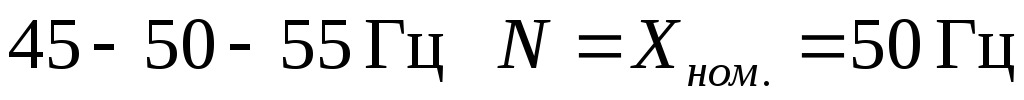 
);
длине шкалы (выраженной в мм), если шкала имеет резко сужающиеся деления (логарифмические, гиперболические шкалы, как, например, шкала омметра).
В последнем случае абсолютную погрешность и длину шкалы выражают в одних единицах (в мм).
Для приборов со шкалой, градуированной в единицах ФВ, для которой принята шкала с условным нулем (например, для приборов, измеряющих температуру в градусах Цельсия), нормирующее значение принимается равным разности конечного и начального значения шкалы (т.е. диапазону измерений 
).
Приведенная погрешность СИ, определяемая в соответствии с (1.43), может иметь любое значение. Но для того, чтобы упорядочить требования к СИ по точности и ограничить номенклатуру их, конкретное значение приведенной погрешности для присвоения СИ класса точности следует выбирать из ряда чисел, регламентированного ГОСТ 13600 – 68 (выбирается ближайшее число со стороны больших значений):
Класс точности указывается в технической документации на СИ и в виде условного обозначения наносится на шкалу или корпус измерительного прибора. Если для СИ нормируется предел допускаемой основной приведенной погрешности в соответствии с (1.43),то условное обозначение класса точности представляет собой само число 
, выраженное в % (например, 0,5 или 2,0) во всех случаях, кроме тех, когда СИ имеет резко нелинейную шкалу. Для СИ с резко нелинейной шкалой (когда нормирующее значение N равно длине шкалы) условное обозначение класса точности имеет вид — 
или 
.
В группе СИ, для которых преобладает мультипликативная составляющая погрешности, предел допускаемой абсолютной погрешности можно записать в виде:
.
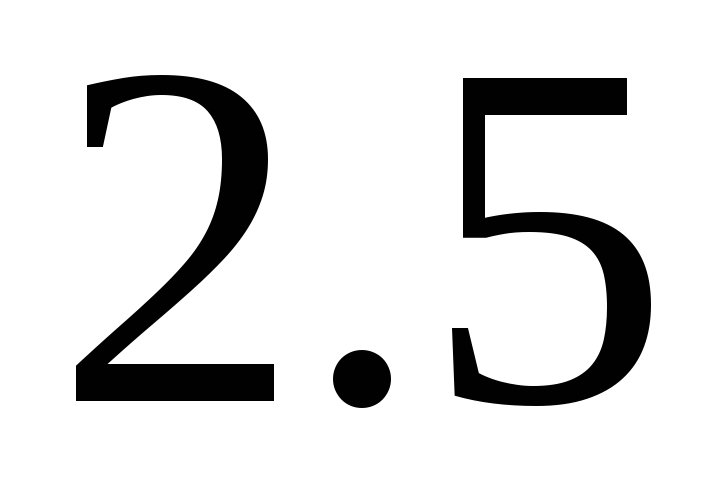
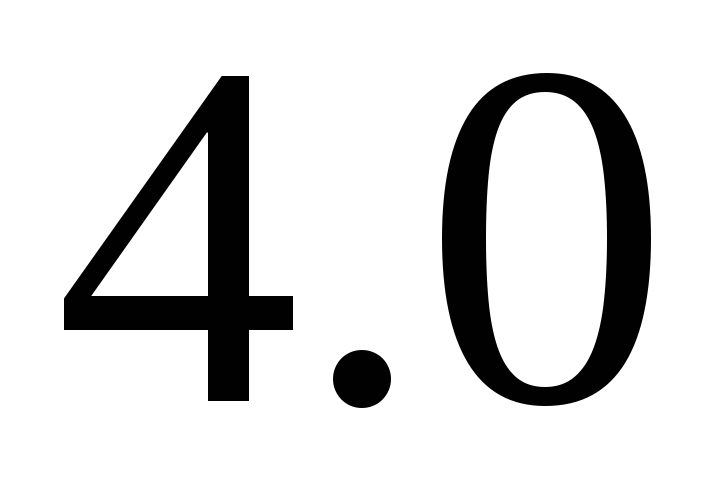
Переходя к относительным погрешностям, получаем, что предел допускаемой основной относительной погрешности для СИ этой группы (в процентах):
, где 
. (1.44)
Для СИ этой группы числовое значениеb, выраженное в процентах выбирается из того же ряда чисел и указывается в технической документации в качестве класса точности. Условное обозначение класса точности на шкале или на корпусе прибора имеет вид — , например.
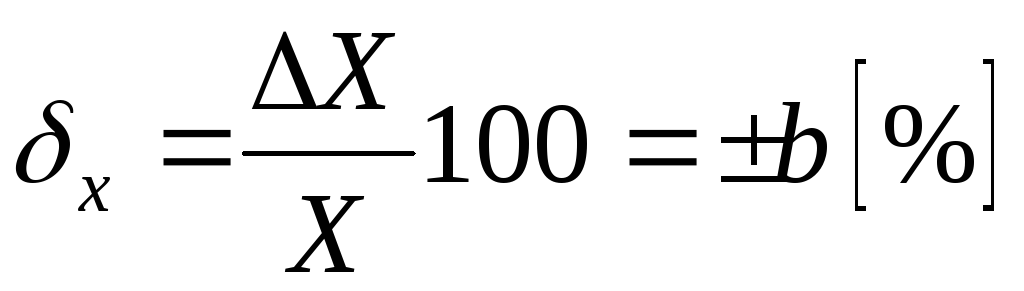
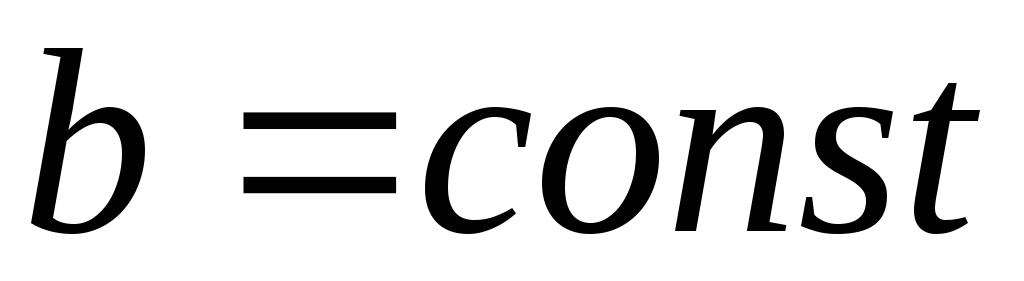
В группе СИ, для которых необходимо учитывать как аддитивную, так и мультипликативную составляющие погрешности, предел допускаемой абсолютной погрешности можно выразить в виде суммы двух членов:
,
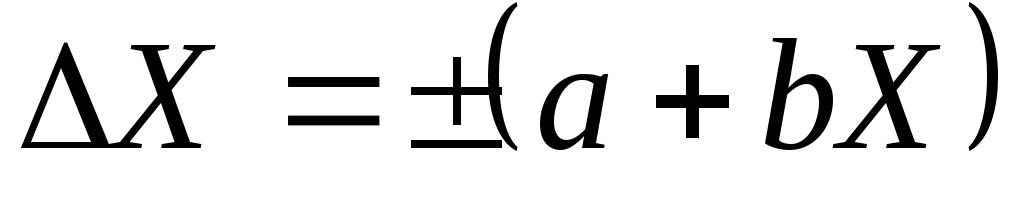
где Х — значение измеряемой величины;
a и b — положительные числа, не зависящие от Х.
Предел допускаемой основной погрешности для приборов этой группы нормируется по величине приведенной погрешности. Нормирующей величиной является конечное значение шкалы — 
, но приведенная погрешность определяется в двух точках шкалы: при 
(начальная отметка шкалы); и при 
(конечная отметка шкалы).
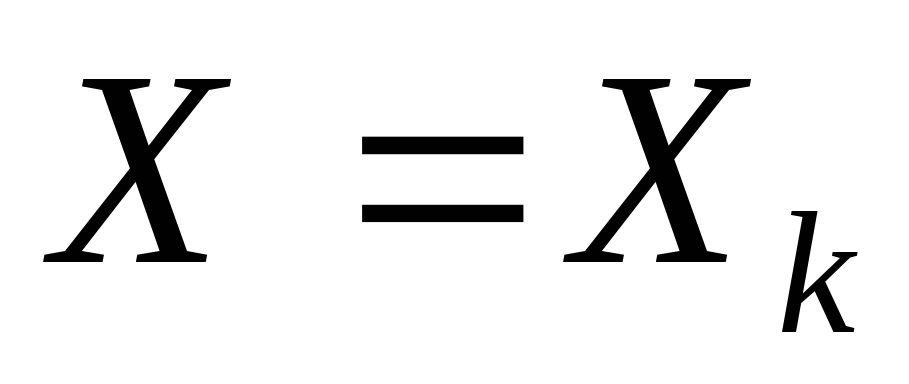
Приведенная погрешность для любой точки шкалы (в процентах):
, (1.45)
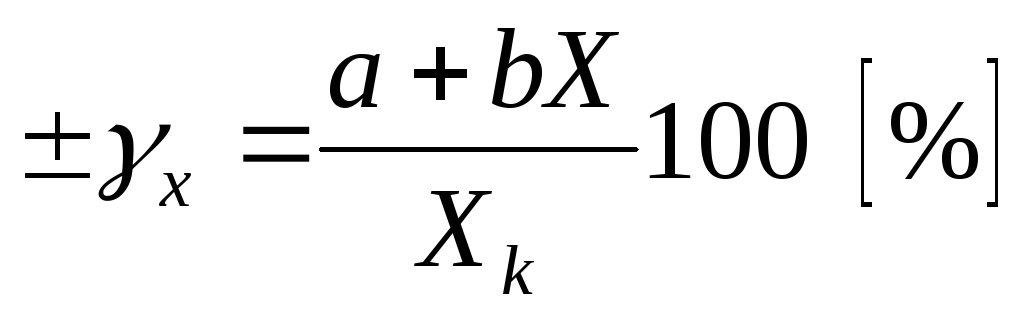
при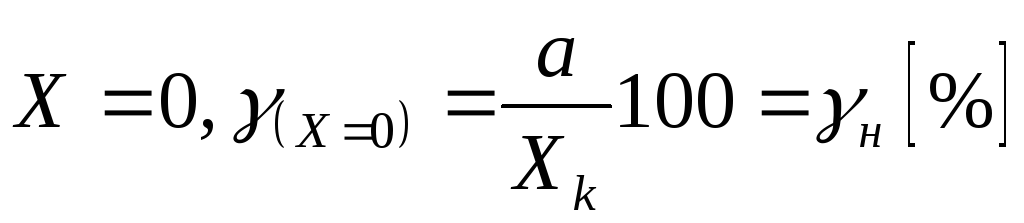 
;
при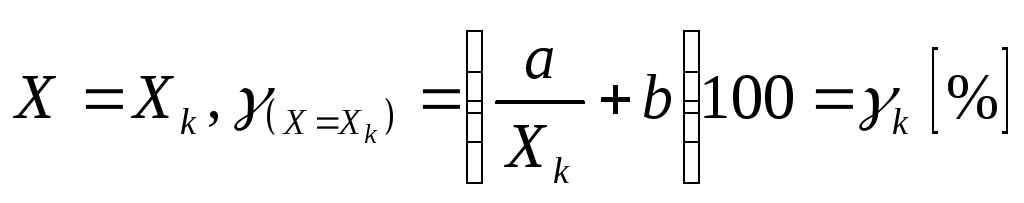 
,
где 
— приведенная погрешность в начале шкалы,
— приведенная погрешность в конце шкалы.
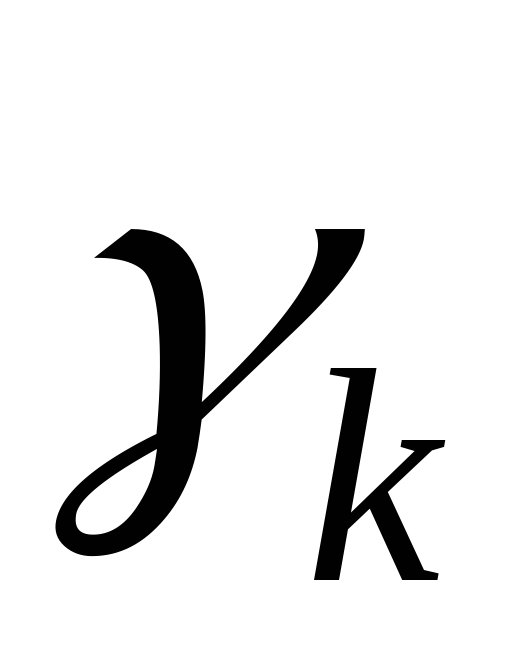
Числовые значения 
и 
, выраженные в процентах, выбираются из ряда чисел, регламентированных ГОСТом, и приводятся в технической документации в качестве класса точности СИ, включающего аддитивную и мультипликативную составляющую погрешности. Условное обозначение класса точности на шкале или на корпусе прибора имеет вид дроби — 
(например, 
).
Для средств измерения этой группы предел допускаемой основной абсолютной и предел допускаемой основной относительной погрешностей могут быть записаны с использованием (1.45) формулами:
(1.46)
где 
— используемый предел измерения;
— результат измерения (отсчет по шкале).
Условные обозначения классов точности и формулы для расчета погрешностей результата измерений сведены в таблицу 1.2.
Рассмотренные четыре способа нормирования предела допускаемой основной погрешности наиболее часто используются для средств электрических измерений, но не исчерпывают всех возможных вариантов нормирования предела допускаемой основной погрешности. В обоснованных случаях ГОСТ разрешает устанавливать предел допускаемой основной погрешности по более сложной формуле, или в виде таблицы, или графика.
Как уже упоминалось, пределы допускаемых дополнительных погрешностей нормируются путем указания их связи с пределом допускаемой основной погрешности. Таким образом, класс точности СИ позволяет оценить как допускаемые пределы основной погрешности, так и допускаемые пределы всех дополнительных погрешностей по отдельности, соответствующие рабочим условиям эксплуатации СИ.
В заключение следует подчеркнуть следующее. Класс точности СИ не является непосредственной характеристикой точности проведенных с помощью него измерений, но класс точности позволяет оценить (рассчитать) погрешность полученного результата. Класс точности является обобщенной характеристикой точности СИ. Допускаемый предел основной погрешности есть предел суммы систематической и случайной составляющих погрешности СИ, но поскольку в техническом описании, как правило, отсутствуют сведения о виде закона распределения случайной составляющей погрешности, принято (если нет других оснований) считать распределение основной погрешности в пределах указанных границ равномерным.
Источник
