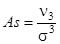Способы нормирования метрологических характеристик средств измерений

Содержание

Нормирование метрологических характеристик средств измерений
Нормирование метрологических характеристик средств измерении осуществляется двумя способами:
32. Нормирование метрологических характеристик средств измерений.
34 Способы нормирования характеристик, определяющих точность измерений. Характеристики статистических распределений.

Нормирование метрологических характеристик средств измерений

Нормирование метрологических характеристик средств измерении осуществляется двумя способами:

1 Путем установления номинальной метрологической характеристики средств измерений данного типа.

2. Путем указания пределов, в которых должно находиться значение нормируемой метрологической характеристики.

Типовые метрологические характеристики групп 1.1 и 2.1 нормируют 1-м способом как номинальные характеристики всех средств измерений данного типа. Номинальную функцию преобразования измерительного преобразователя представляют в виде формулы, таблицы, графика. Линейную функцию преобразования, проходящую через начало координат, допускается представлять коэффициентом преобразования в виде числа. Номинальные значения однозначной или многозначной меры представляют именованными числами.

Для конкретных экземпляров средств измерений, предназначенных для применения не с номинальными (распространяющимися на все экземпляры средств измерений данного типа), а с индивидуальными метрологическими характеристиками, полученными, например, в результате калибровки, соответствующие номинальные характеристики можно не нормировать. В этих случаях обычно применяют 2-й способ нормирования и указывают пределы (граничные характеристики), в которых должна находиться индивидуальная метрологическая характеристика при предусмотренных условиях применения данного средства измерений.

Нормальные и рабочие условия применения средств измерений устанавливаются в нормативно-технических документах на средства измерений. Нормальными считаются условия, при которых зависимостью метрологических характеристик от изменения значений влияющих величин можно пренебречь. Так, для многих типов средств измерений нормальными условиями являются: температура — (293 ± 5) К, относительная влажность — (65 ± 15) %, напряжение в сети питания — 220 В ± 10 %. Рабочие условия отличаются от нормальных более широким диапазоном изменения значений влияющих величин.

При нормировании метрологических характеристик группы 1.2 исходят из того, что правшьпость показаний средств измерений обеспечивается поправкой, точное значение которой для каждого конкретного экземпляра средств измерений неизвестно. Поэтому устанавливают пределы, в которых должна находиться поправка у всех средств измерений данного типа. Прибегают также к ситуационному моделированию и нормируют пределы, в которых должны находиться аналоги числовых характеристик ситуационной модели.

Точность показаний нормируется указанием предельно допустимого значения среднего квадратического отклонения (или его оценки).

Так как показание и поправка суммируются, то может нормироваться аналог среднего квадратического отклонения композиции закона распределения вероятности показания и ситуационной модели поправки.

Нормирование метрологических характеристик группы 1.2 может производиться как для нормальных, так и для рабочих условий. Они представляются либо одним числом, либо функцией (формулой, таблицей, графиком) информативного параметра входного или выходного сигнала.

При нормировании метрологических характеристик группы 1.3 устанавливаются номинальная динамическая характеристика, пределы допускаемых отклонений от нее и граничные динамические характеристики. Они представляются в виде числа, формулы, таблицы или графика.

Во всех случаях представление нормированных метрологических характеристик в виде графика допускается только при одновременном представлении их в виде формулы или таблицы.

Динамические характеристики средств измерений нормируются для нормальных или для рабочих условий применения. В отличие от этого метрологические характеристики группы 2.2 нормируются только для рабочих условий измерений. В рабочих условиях изменение значений влияющих величин начинает сказываться на точности и правильности показаний. Это учитывается функциями влияния. Для разных экземпляров средств измерений данного типа могут различаться как вид этих функций, так и их параметры. Однако в принципе, для всех экземпляров средств измерений данного типа эти функции должны бьггь подобны, а их параметры близки. Поэтому нормируются в качестве номинальных некоторые усредненные функции влияния с указанием их параметров. Нормируются также пределы допускаемых отклонений функций влияния у отдельных экземпляре средств измерений данного типа от номинальной. Если функции влияния у различных экземпляре срдств измерений данного типа существенно различаются между собой, то нормируются граничные функции влияния.

В нормативно-технических документах номинальная функция влияния, пределы допускаемых отклонений от нее и граничные функции влияния представляются в виде числа, формулы, таблицы или графика. Линейную функцию влияния, проходящую через начало координат, допускается представлять коэффициентом влияния в виде числа. Функции влияния прдставляют в координатах, у которых начало отсчета по оси ординат совпадает с нормальным значением влияющей величины на оси абсцисс.

Пределы допускаемых изменений метрлогических характеристик, вызванных изменениями влияющих величин, устанавливают в виде границ зоны вокруг значения метрлогической характеристики при нормальных условиях.

Метрологические характеристики группы 2.3 нормируют для нормальных или рабочих условий путем установления номинальных характеристик и прееделов допускаемых отклонений от них или граничных характеристик. Неинформативные параметры выходного сигнала средства измерений (группа 2.4) нормируют для рабочих условий путем установления номинальных параметров и пределов допускаемых отклонений от них либо наибольших или наименьших допускаемых значений параметров. Формы представления характеристик, относящихся к группам 2.3 и 2.4, устанавливаются в стандартах на средства измерений конкретных видов или типов.

В зависимости от особенностей использования средств измерений может возникнуть необходимость в том или ином наборе их метрологических характеристик. Так, для вещественных мер и цифроаналоговых преобразователей, аналоговых и цифровых измерительных показывающих и регистрирующих приборов, аналоговых и аналого-цифровых измерительных щхюбразователей нормируются разные наборы метрологических характеристик. Поэтому в нормативно-технических документах на средства измерений конкретных видов или типов следует нормировать комплексы метрологических характеристик из числа установленных в ГОСТ 8.009-84(2003) и (или) в необходимых случаях дополнительно включенных, исходя из специфики назначения средств измерений и технико-экономического обоснования. Рациональность комплекса нормированных метрологических характеристик проверяется при испытаниях средств измерений по ПР 50.2.009-94. Эта проверка должна быть включена в программы испытаний.

Источник

32. Нормирование метрологических характеристик средств измерений.

Под нормированием метрологических характеристик понимается количественное задание определенных номинальных значений и допустимых отклонений от этих значений.

Общий перечень основных нормируемых метрологических характеристик средства измерения, формы их представления и способы нормирования установлены в ГОСТ 8.009-72. В него входят:

пределы измерений, пределы шкалы;

цена деления равномерной шкалы аналогового прибора или многозначной меры, при неравномерной шкале – минимальная цена деления;

выходной код, число разрядов кода, номинальная цена единицы наименьшего разряда цифровых средств измерений;

номинальное значение однозначной меры, номинальная статическая характеристика преобразования измерительного преобразователя;

погрешность средств измерений;

вариация показаний прибора или выходного сигнала преобразователя;

полное входное сопротивление измерительного устройства;

полное выходное сопротивление измерительного преобразователя или меры;

неинформативные параметры выходного сигнала измерительного преобразователя или меры;

динамические характеристики средств измерений;

наибольшие допустимые изменения метрологических характеристик средств измерений в рабочих условиях применения.

Одной из основных метрологических характеристик измерительных преобразователей является статическая характеристика преобразования. Она устанавливает зависимость информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра входного сигнала.

Основные нормируемые метрологические характеристики СИ.

Смотри 21 вопрос

Типовые характеристики, предназначенные для определения результатов измерений, нормируют как номинальные характеристики средств измерений данного типа.

34 Способы нормирования характеристик, определяющих точность измерений. Характеристики статистических распределений.

Статистическое распределение содержит полную информацию о вариации изучаемого признака. Но построение вариационного ряда оказывается недостаточным, когда возникает задача сравнения вариации в двух и более статистических совокупностей. Определенные выводы можно сделать, изучая графическое изображение вариационного ряда. С целью более полного и точного описания совокупности необходимо дополнить графический анализ небольшим количеством сводных характеристик распределения, вычисленных с использованием вариантов и их частот. Эти характеристики должны отражать присущие изучаемой совокупности закономерности и тенденции.

Для описания статистических распределений обычно используются три вида характеристик: 1) средние или характеристики центральной тенденции; 2) характеристики изменчивости (вариации) признака; 3) характеристики, отражающие дополнительные особенности распределений, в частности их форму.

Средние характеристики.Средняя характеризует типичный для совокупности размер признака, т.е. центральную тенденцию в распределении. Практическое использование такой характеристики целесообразно в том случае, когда отдельные варианты ряда распределения концентрируются вблизи некоторого значения. Если же совокупность неоднородна, результаты наблюдений значительно отличаются друг от друга и не обнаруживают общей тенденции, то использование средней становится формальным.

Средние величины имеют ту же размерность, что и изучаемый признак. Существуют различные формы средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая и т.д.

Средняя арифметическая. Наиболее распространенным видом средней является средняя арифметическая, которая вычисляется по формуле

, (9.1)

Если по наблюдениям составлен вариационный ряд, то следует использовать следующую формулу:

(9.2)

где х_і – варианты признака в дискретном или середины интервалов в интервальном рядах, f_i – соответствующие частоты, k – количество вариантов или интервалов, n – объем совокупности. Величины f_i в этой формуле часто называют весами, а саму характеристику, вычисленную по формуле (9.2) –взвешенной.

Если по данным наблюдений построен дискретный вариационный ряд, то формулы (9.1) и (9.2) дают одинаковые значения средней арифметической. Если же построен интервальный ряд, то средние арифметические, вычисленные по формулам (9.1) и (9.2), как правило, не совпадают, т.к. в формуле (9.2) значения признака внутри каждого интервала принимается равными серединам интервалов. Однако ошибка, возникающая в результате такой замены, будет мала, если наблюдения распределены равномерно внутри каждого интервала и не скапливаются к одноименным границам интервалов (т.е. либо все к нижним границам, либо все к верхним границам).

Средняя арифметическая применяется в том случае, когда сумма наблюдений должна остаться неизменной, если каждое из них заменить средней арифметической.

Наряду со средними в качестве характеристик центра распределения применяются так называемые структурные средние – мода и медиана.

Мода. Модой называется значение признака, которому соответствует наибольшая частота, т.е. которое наблюдалось наибольшее число раз.

Для дискретного ряда мода находится непосредственно из распределения частот.

Если составлен интервальный вариационный ряд, то мода вычисляется по следующей приближенной формуле:

где x₀ – начало модального интервала, т. е. интервала, имеющего максимальную частоту, h – длина модального интервала, f_i – частота модального интервала, f_{i –}₁и f_{i +}₁ – частоты соответственно предшествующего и последующего за модальным интервалов.

Распределение, имеющее одну моду называется унимодальным; две моды – бимодальным; три и более мод – мультимодальным.

Медиана.Медианой называется значение признака, приходящееся на середину ранжированного ряда наблюдений.

Если проведено нечетное число наблюдений, т.е. n=2k+1, kÎZ, и результаты наблюдений размещены по возрастанию, то медиана равна:

Если проведено четное число наблюдений, т.е. n=2k, kÎZ, то на середину ранжированного ряда приходятся значения x_k и x_k₊₁. В этом случае в качестве медианы принимают среднее арифметическое двух серединных элементов, т.е.

Если составлен интервальный вариационный ряд, то медиана вычисляется по следующей формуле:

где x₀ – начало мeдианного интервала, т. е. интервала, в котором эмпирическая функция распределения принимает значение 0.5, h – длина медианного интервала, n – объем выборки, Т_і_–1–сумма частот интервалов, предшествующих медианному; f_i – частота медианного интервала.

Следует отметить, что средняя арифметическая и медиана могут не являться элементами распределения, в то время как модой обязательно является одно или несколько значений изучаемого признака.

Характеристики вариации.Рассмотренные выше характеристики центра статистической совокупности тем более характерны для данного распределения, чем ближе группируются наблюдения вокруг средней арифметической, т.е. чем менее они рассеяны. Поэтому средние характеристики должны быть дополнены измерением вариации признака относительно средней, т.е. характеристиками изменчивости наблюдавшихся значений признака.

Простейшим измерителем вариации является размах варьирования R, т.е. разность между наибольшим и наименьшим значением признака: R= x_max–x_min. Размах варьирования дает лишь приближенное представление о вариации признака и, кроме того, на крайние значения ряда распределения могут влиять различные случайные факторы, что делает их весьма ненадежными.

Выше отмечалось, что наибольший интерес представляет группировка значений признака около средней арифметической. Отклонения вариантов от средней арифметической определяют разности (x_i– ), а веса вариантов – как часто имеют место эти разности в данном распределении. Однако сумма произведений отклонений на их веса не может являться мерой рассеяния признака, т.к. по доказанной выше теореме эта сумма всегда равна нулю. Для устранения влияния знака отклонений переходят либо к абсолютным величинам отклонений, либо к квадратам отклонений, получая при этом различные характеристики вариации признака.

Среднее линейное отклонение. Средним линейным отклонением вариационного ряда называется средняя арифметическая абсолютных величин отклонений вариантов от их средней арифметической:

Дисперсия выборки. Дисперсией s 2 называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:

; (9.3)

где х_і – элемент совокупности, n – ее объем, – средняя арифметическая.

Если по наблюдениям построен вариационный ряд, то применяют формулу:

, (9.4)

Загрузка.

Стандартное отклонение.При вычислении дисперсии суммируются квадраты отклонений вариантов, в силу чего дисперсия измеряется в квадратах тех единиц, в которых измеряется изучаемый признак. Для того, чтобы характеристика вариации выражалась в тех же единицах, что и значения признака, используют корень квадратный из дисперсии.

Средним квадратическим отклонением (стандартным отклонением) называется арифметическое значение корня квадратного из дисперсии:

. (9.5)

Коэффициент вариации. Для сравнительной оценки вариации в распределениях с различными значениями средней используется также коэффициент вариации, равный выраженному в процентах отношению среднего квадратического отклонения к средней арифметической:

Коэффициент вариации позволяет определить, насколько хорошо средняя арифметическая представляет все элементы статистической совокупности. Если V 33%, то, как правило, можно сделать вывод о неоднородности статистической совокупности и средняя арифметическая не является типичным значением для всех элементов. Однако коэффициент вариации теряет смысл при =0 и становится малонадежным при близких к нулю значениях средней.

Характеристики формы.Если полигон вариационного ряда скошен в ту или иную стороны от средней арифметической, то такой ряд называют асимметричным. В качестве меры асимметрии вариационного ряда используется коэффициент асимметрии.

Коэффициентом асимметрии вариационного ряда называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

Если коэффициент асимметрии As 0. Для симметричного распределения варианты, равноудаленные от средней , имеют одинаковые частоты, и поэтому n₃=0, следовательно, As=0

Источник