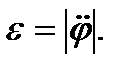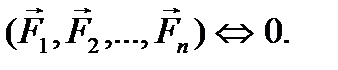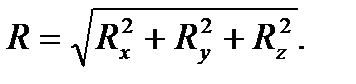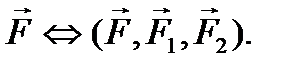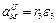Вычисление угловой скорости и углового ускорения тела при плоском движении
Как видно из выше изложенного, при вычислении скоростей и ускорений точек тела при плоском движении важно уметь найти угловую скорость и угловое ускорение тела. Остановимся на этом отдельно.
Основные способы вычисления угловой скорости
1. Если заданы кинематические уравнения плоского движения тела (41),то угловую скорость можно вычислить согласно ее определению
2. Если известны скорость какой-либо точки тела и положение МЦС, то угловая скорость может быть найдена по формуле (48)
Направление угловой скорости в этом случае определяется направлением вектора 
(см. рис. 46).
3. Угловая скорость может быть также найдена, если известна скорость при относительном вращении какой-либо точки В вокруг полюса А. В этом случае
Направление угловой скорости здесь должно быть согласовано с направлением вектора относительной скорости 
(см. рис. 47).
Основные способы вычисления углового ускорения
1. Если заданы кинематические уравнения движения тела (41), то угловое ускорение найдется согласно определению
2. Если угловая скорость была найдена по формуле (48)
и расстояние от точки А до мгновенного центра скоростей не изменяется при движении тела (AP=const), то, дифференцируя по времени последнее выражение для углового ускорения, получим
Проиллюстрируем этот способ нахождения углового ускорения тела примером. Пусть колесо катится по горизонтальной поверхности без скольжения. Для центра колеса С заданы скорость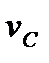 
и ускорение 
(см. рис. 48).
Угловая скорость колеса в этом случае найдется по формуле
и в соответствии с направлением вектора 
будет направлена по часовой стрелке. Расстояние от точки С до мгновенного центра скоростей при движении колеса не меняется и равно радиусу колеса CP=R. Тогда угловое ускорение колеса можно найти по формуле
Так как по условию качение колеса является замедленным, то направление углового ускорения будет противоположно направлению угловой скорости (см. рис. 48).
3.Если известно тангенциальное ускорение какой-либо точки В тела при ее относительном вращении вокруг полюса А 
, то угловое ускорение тела найдется по формуле
Этот способ вычисления ε использовался при нахождении углового ускорения шатуна АВ в примере 7.
Раздел 2. СТАТИКА
Статика – это раздел механики, в котором изучается равновесие материальных объектов под действием приложенных сил.
Глава 1. ВВЕДЕНИЕ В СТАТИКУ
Основные понятия
Силой называется векторная величина, характеризующая механическое воздействие одного материального объекта на другой.
Сила характеризуется точкой приложения, направлением действия и численной величиной (модулем).
Совокупность сил, действующих на выбранный материальный объект, называется системой сил.
На рис. 49 изображена система сил, приложенных к некоторому телу.
Будем обозначать систему сил 
Две системы сил называются эквивалентными, если, будучи приложенными к твердому телу по отдельности, они сообщают ему одно и то же движение из состояния покоя. Эквивалентность систем сил обозначается знаком 
:
Система сил называется уравновешенной (или эквивалентной нулю), если она, будучи приложенной к твердому телу, не сообщает ему движения из состояния покоя. Уравновешенную систему сил обозначают следующим образом:
Главным вектором системы сил (обозначается 
) называется вектор, равный геометрической сумме всех сил, входящих в систему:
(55)
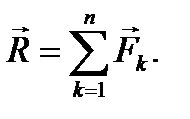
На рис. 50 показано геометрическое построение главного вектора системы
сил. На практике такой способ неудобен и для нахождения главного вектора равенство (55) записывают в проекциях на выбранные оси координат
после чего величину главного вектора вычисляют по теореме Пифагора
Равнодействующей силой данной системы сил (обозначается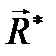 
) называется сила, эквивалентная этой системе сил:
Отметим, что не всякая система сил имеет равнодействующую.
Тело называется свободным, если ничто не препятствует его перемещению в пространстве.
В противном случае тело называется несвободным.
Материальные объекты, ограничивающие перемещение несвободного тела, называются связями.
Силы, с которыми связи действуют на несвободное тело, называются реакциями связей или пассивными силами.
Остальные силы, не являющиеся реакциями связей, называются активными силами.
Активные силы могут сообщать свободному телу движение, они имеют определенный источник действия, не зависят наложенных связей и обычно считаются известными при решении задач.
Реакции связей зависят от активных сил, действующих на несвободное тело, они могут изменять свою величину и направление при изменении активных сил.
Аксиомы статики
Все основные методы изучения движения и равновесия тел в теоретической механике могут быть строго доказаны математически, исходя из нескольких основных положений, называемых аксиомами. Сами аксиомы сформулированы на основании многовекового опыта человечества. Далее приведем формулировки аксиом статики и дадим необходимые пояснения.
П е р в а я а к с и о м а . Система из двух сил, равных по величине и направленных в противоположные стороны вдоль одной прямой, является уравновешенной.
Эта аксиома справедлива для сил, приложенных к одному абсолютно твердому телу.
В т о р а я а к с и о м а. Механическое состояние тела не изменится, если к действующей на него системе сил добавить или изъять уравновешенную систему сил.
Исходя из приведенных выше двух аксиом, докажем следствие.
Любую силу, не нарушая ее действия на абсолютно твердое тело, можно переносить вдоль линии действия силы.
Рассмотрим абсолютно твердое тело, на которое в точке А действует сила 
. Возьмем уравновешенную систему сил 
, равных по величине силе 
и направленных в противоположные стороны по линии действия силы . Приложим обе эти силы в точке В на линии действия силы (см. рис. 51).
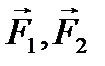
Тогда по второй аксиоме
Но по первой аксиоме силы 
образуют уравновешенную систему и по второй аксиоме их можно отбросить. В результате получим
что и доказывает следствие.
Т р е т ь я а к с и о м а (закон равенства действия и противодействия). Два тела взаимодействуют с другом с силами, равными по величине и противоположно направленными вдоль одной прямой.
Заметим, что эти силы не будут уравновешенными, так как они приложены к разным телам.
Ч е т в е р т а я а к с и о м а (аксиома параллелограмма сил). Система из двух сил, приложенных в одной точке тела, имеет равнодействующую силу, равную геометрической сумме двух данных сил.
Эту аксиому можно выразить формулой 
и пояснить рисунком
Величину равнодействующей можно вычислить по формуле
Данная аксиома допускает и обратное утверждение: силу можно по правилу параллелограмма разложить бесчисленным множеством способов на две силы.
При этом составляющие силы могут располагаться в любой одной плоскости, проходящей через линию действия разлагаемой силы.
П я т а я а к с и о м а (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если связи мысленно отбросить и заменить их действие соответствующими реакциями.
Ш е с т а я а к с и о м а (аксиома отвердевания). Равновесие механической системы не нарушится от наложения новых связей. В частности, равновесие деформируемого тела не нарушится, если оно станет абсолютно твердым.
При этом под механической системой подразумевается выделенная совокупность материальных точек и тел.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Источник
ОСНОВНЫЕ СПОСОБЫ ВЫЧИСЛЕНИЯ УГЛОВОГО УСКОРЕНИЯ ПРИ ПЛОСКОМ ДВИЖЕНИИ
При вычислении ускорений точек фигуры при плоском движении необходимо знать угловое ускорение. Рассмотрим некоторые приемы его определения.
1.Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение ε определяем путем дифференцирования их по времени, т.е.
2. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени, считая ее для вывода формулы известной функцией времени. Угловую скорость можно найти по формуле (7)
ω= vA/AP где А-точка плоской фигуры; Р мгновенный центр скоростей .Дифференцируем ω по времени, получаем
Так, например, при качении колеса без скольжения по неподвижной прямой линии (см. рис. 55), если за точку А взять центр колеса О, то, учитывая, что он движется прямолинейно, получим: ε= ao/R, так как в этом случае
где R — радиус колеса.
При качении без скольжения одного колеса по неподвижному другому колесу сначала установим зависимость между угловой скоростью ω1 подвижного колеса и угловой скоростью ю кривошипа ОА (рис. 61). Учитывая, что мгновенный центр скоростей подвижного колеса лежит в точке соприкосновения колес,
где R — радиус неподвижного колеса; r—радиус подвижного колеса. Дифференцируя по времени (21), имеем
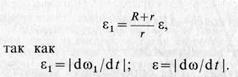
Из сравнения (21) и (22) видно, что связь между угловыми скоростями и угловыми ускорениями колес полностью аналогична. Это справедливо и для углов поворота колес, если нулевые их значения выбрать в один и тот же момент времени.
При внешнем зацеплении дуговые стрелки угловой скорости и углового ускорения подвижного колеса совпадают с дуговыми стрелками соответственно угловой скорости и углового ускорения кривошипа ОА. При внутреннем зацеплении колес дуговые стрелки ε и ω колеса и кривошипа имеют противоположные направления.
3. Иногда угловое ускорение е можно найти путем проецирования на оси координат известного по направлению ускорения, например точки В, если ускорение какой-либо яругой точки А и угловая скорость фигуры ω известны или их можно вычислить предварительно.
Так, если ускорение точки В
то, проецируя обе части (23) на ось Ох, перпендикулярную ускорению ав, получаем соотношение, из которого можно определить угловое ускорение, если другие величины, входящие в это соотношение, известны.
Задание для выполнения по разделу кинематика
II. Определение скорости и ускорения точки по заданным уравнениям
ее движения. Задание К.1.
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в табл. 1.
| Номер варианта | Уравнения движения | t1, c |
| x=x(t), см | y=y(t), ñì | |
| -2t 2 +3 | -5t | 1,5 |
| 4соs 2 (pt/2)+2 | 4sin 2 (pt/2) | |
| -cos(pt 2 /3)+3 | sin(pt 2 /3)-l | |
| 4t+4 | -4/(t+1) | |
| 2sin (pt/2) | -3соз(pt/2)+4 | |
| 3/t 2 +2 | -4/t | 1,5 |
| 3t 2 -t+1 | 5t 2 -5t/2-2 | |
| 7sin(pt 2 /4)+3 | 2-7cos(pt 2 /4) | |
| -3/(t+2) | 3t+6 | |
| -4cos(pt/2) | -2sin(pt/2)-3 | |
| -4/t 2 +1 | -3/t | 1,5 |
| 5sin 2 (pt/4) | 5cos 2 (pt/4)-3 | |
| 5cos(pt 2 /3) | -5sin(pt 2 /3) | |
| -2t-2 | -2/(t+l) | |
| 4соs(pt/2) | -3sin(pt/2) | |
| 3t | 4t 2 +1 | 1,5 |
| 7sin 2 (pt/4)-5 | -7cos 2 (pt/4) | |
| 1+3cos(pt 2 /3) | 3+3cos(pt 2 /3) | |
| 4t 2 -4 | 3t | |
| 2-3t-6t 2 | 3-3t/2-3t 2 | |
| 6sin (t 2 /4)-2 | 6cos(pt 2 /4)+3 | |
| 7t 2 -3 | 5t | 0,75 |
| 4-3t 2 | 4-5t 2 -5t/2 | |
| -4cos(pt/2)-1 | -4sin(pt/2) | |
| -6t | -2t 2 -4 | |
| 8cos 2 (pt/4)+2 | 8sin 2 (pt/4)-7 | |
| -3-9sin(pt 2 /4) | -9cos(pt 2 /4)+5 | |
| -4t 2 +1 | -3t | |
| 5t 2 + 5t/2-3 | 3t 2 +t+3 | |
| 2cos(pt 2 /3)-2 | 2sin(pt 2 /3)+3 |
Пример выполнения задания. Исходные данные:
| x = 4t; у=16t 2 -1; t1 = 0,5 (х и у — в см, t и t1 — в с). | (1) |
| Решение. Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений (1). Получаем у = х 2 — 1, т. е. траекторией точки является парабола, показанная на рис. 6. Вектор скорости точки |  |
| Рис. 6 | |
 | (2) |
 |
Здесь 
— орты осей x и у; 
— проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
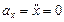 |  | (3) |
 |  |
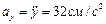По найденным проекциям определяются модуль скорости:
 | (4) |
и модуль ускорения точки:
 | (5) |
Модуль касательного ускорения точки
 | (6) |
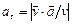 | (6`) |
 | 6« |
выражает проекцию ускорения точки на направление ее скорости. Знак “+” при означает, что движение точки ускоренное, направления 
и 
совпадают; знак “-” — что движение замедленное.
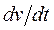
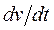
Модуль нормального ускорения точки
 | (7) |
Если радиус кривизны траектории r в рассматриваемой точке неизвестен, то 
можно определить по формуле
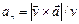 | (8) |
При движении точки в плоскости формула (8) принимает вид
 | (8`) |
Модуль нормального ускорения можно определить и следующим образом :
 | (9) |
После того как найдено нормальное ускорение по формулам (8) или (9), радиус кривизны траектории в рассматриваемой точке определяется из выражения
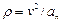 | (10) |
Результаты вычислений по формулам (3)-(6), (8) и (10) для заданного момента времени t1 =0,5 с приведены в табл. 2.
| Координаты, см | Скорость, см/с | Ускорение, см/с 2 | Радиус кривизны, см | |||||||
| x | y | vx | vy | v | ax | ay | a | at | an | r |
| 2,0 | 3,0 | 4,0 | 16,5 | 32,0 | 32,0 | 31,0 | 7,8 | 35,0 |
На рис. 6 показано положение точки М в заданный момент времени. Вектор v строим по составляющим vx и vy причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор а строим по составляющим ax и ay и затем раскладываем на составляющие an и at. Совпадение величин an и at найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 1) добавляется третье уравнение (табл. 3).
Общий порядок выполнения задания в этом случае такой же, как и в приведенном выше примере.
| № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см | № варианта | z=z(t), см |
| 3t | 3t | 2t | 1,5t | 4t | 6t | ||||||
| 2t | 2,5t | 3t | 5t | t | 3,5t | ||||||
| 1,5t | 5t | 1,5t | 3,5t | 1,5t | 4t | ||||||
| 4t+4 | 4t+8 | 2t+2 | 6t | 6t | 5t | ||||||
| t | T | 3t | 2t | 2t | 1,5t |
III. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях. Задание К.2.
Движение груза 1 должно описываться уравнением
| х = c2t 2 + c1t + с0, | (1) |
где t — время, с; с0-2 — некоторые постоянные.
В начальный момент времени (t=0) координата груза должна быть х0, а его скорость — v0.
Кроме того, необходимо, чтобы координата груза в момент времени t = t2 была равна х2.
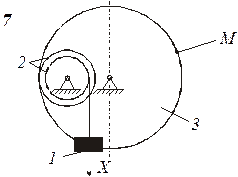
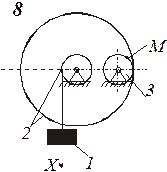
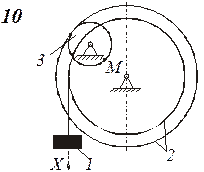
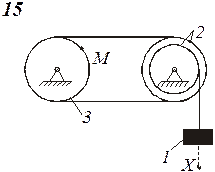
Определить коэффициенты с0, с1 и c2 при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1 скорость и ускорение груза и точки М одного из колес механизма.
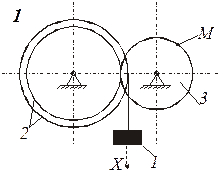
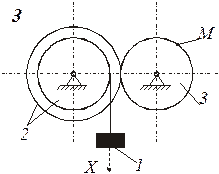
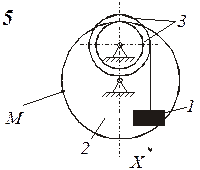
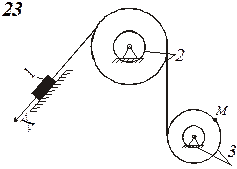
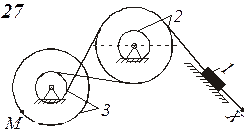
Схемы механизмов показаны на рис. 8-10, а необходимые данные приведены в табл. 4.
| Номер варианта (рис.2-4) | Радиусы, см | Координаты и скорости груза 1 | Расчетные моменты времени, с | |||||
| R2 | r2 | R3 | r3 | x0, см | v0, см/с | x2, см | t2 | t1 |
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| _ | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — | ||||||||
| — |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
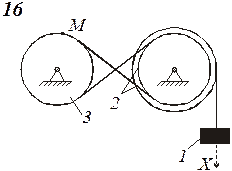Пример выполнения задания. Дано: схема механизма (рис.7); R2=50 см, r2=25 см, R3=65 см, r3=40 см, x0=14 см, v0=5 см/с, x2=168 см, t1=1 с, t2=2 с.
| Найти уравнение движения груза, а также скорости и ускорения груза и точки М в момент времени t=t1. Решение. Уравнение движения груза 1 имеет вид x=c2t 2 +c1t+c0 (1) Коэффициенты с0, с1 и с2 могут быть определены из следующих условий: |  | ||
| Рис. 7 | |||
| при t = 0 | х0 = 14 см |  = 5 см/с | (2) |
| при t2 = 2с | х2 = 168 см | (3) |
Скорость груза 1
v = 
= 2c2t + c1. (4)
Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты
Таким образом, уравнение движения груза 1
х = 36t 2 + 5t + 14. (5)
Скорость груза 1
v = = 72t + 5. (6)
Ускорение груза 1
а = 
= 72 см/с 2 .
Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колес w2 и w2 .В соответствии со схемой механизма
| v=r2w2, R2w2=R3w3 | (7) |
или с учетом (6) после подстановки данных
Угловое ускорение колеса 3
e3= 
=2,215 рад/с 2 .
Скорость точки М, ее вращательное, центростремительное и полное ускорения определяются по формулам
; 
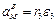
Источник
