Как найти площадь прямоугольника 3 класс
Названия геометрических фигур происходят от количества их сторон. Например, треугольник, четырехугольник, пятиугольник. Но есть фигуры, которые названы по другим признакам, например, прямоугольник, квадрат, ромб, трапеция. Все эти фигуры — четырехугольники, но отличаются друг от друга величиной углов и сторон.
Прямоугольник — четырехугольник с разными сторонами у которого все углы по 90 о .
Квадрат — прямоугольник, у которого все углы по 90 градусов и стороны равные.
Такие отличия есть и у других фигур, например, треугольники подразделяются на прямоугольные, равносторонние, равнобедренные и разносторонние. Свойства фигуры зависят как от количества сторон, так и от других характеристик — величины углов и сторон. Только измерив все параметры, можно точно описать фигуру и определить, какими формулами и правилами пользоваться при вычислениях.
Под этим термином понимают часть плоскости, ограниченной несколькими замкнутыми (соединенными) линиями. В результате соединения линий образуется отрезки, которые называются сторонами фигуры и точки соприкосновения, которые носят название вершин. У треугольника три стороны и три вершины, у четырехугольника — четыре стороны и четыре вершины.
В геометрии есть фигуры, которые выпадают из этого ряда. Это точка, прямая линия, отрезок, луч. Отличаются они от остальных фигур, тем, что не занимают никакой площади, это просто части линии.
Что такое площадь
Теперь рассмотрим еще одно понятие геометрии — площадь. Это часть плоскости, которая находится внутри многоугольника. Другими словами, все, что находится между сторонами фигуры и является ее площадью. Геометрия — часть математики, то есть, наука точная, которая стремится все измерить и описать цифрами. Не стала исключением и площадь. Часть плоскости, которая находится внутри фигуры, разбили на маленькие части с равными сторонами, идущими под прямым углом друг к другу. Такая фигура называется квадрат.
Квадрат — геометрическая фигура из четырех равных сторон и четырех прямых углов.
За единицу площади взяли квадрат, сторона которого равна единице длины (1 миллиметр, 1 метр, 1 сантиметр). Площадь, которую занимает квадрат со стороной 1 сантиметр назвали квадратный сантиметр (обозначает см 2 ). Если квадрат построен из сторон в 1 м, то его площадь 1 м 2 . Найти площадь фигуры — значит определить, сколько таких квадратиков можно поместить внутри фигуры.
Расчет площади прямоугольника
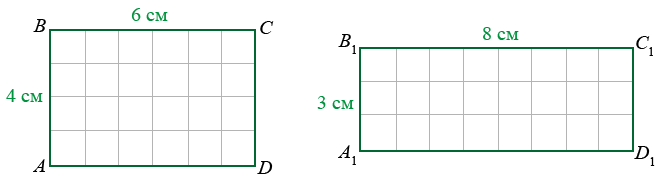
Разберем простую задачу — как высчитать площадь прямоугольника? Можно решить ее двумя способами. Самый простой, но самый длинный и трудоемкий — нарисовать прямоугольник и с помощью карандаша и линейки разбить его на маленькие квадратики. Затем посчитать количество квадратиков и узнать, сколько их поместилось внутри.
Такой способ простой и доступный, если длина сторон прямоугольника — целое количество сантиметров или метров. А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
Ученые древности, идя таким путем заметили интересную особенность, если посчитать квадраты внутри фигуры и сравнить их с результатом умножения длин сторон прямоугольника, то они окажутся одинаковыми. Проверив это на многих прямоугольниках и квадратах составили правило:
Площадь прямоугольника равна длине умноженной на ширину.
В учебниках можно найти и другую формулировку — площадь прямоугольника равна произведению соседних сторон, или еще иначе — площадь прямоугольника равна произведению основания на высоту. Суть этих утверждений одна и та же. Выражается она в формуле:
S=AB ∙BC.
Как уже говорилось, площадь измеряется в квадратных единицах — метрах, сантиметрах, дециметрах. Результат может быть как целым, так и дробным, например, 4 см 2 , 6 см 2 , или 4,6 см 2 (4см 2 и 6мм 2 ).
Использование этой формулы — самый простой способ, как вычислить площадь прямоугольника с разными сторонами. Подходит он и для решения задачи вычисления квадрата (прямоугольника с равными сторонами). Для квадрата формула может выглядеть несколько иначе.
S=АВ 2
Как она получалась? Начнем с основной формулы S=AB ∙BC. У квадрата АВ=ВС, отсюда S= АВ ∙ АВ = АВ 2 .
Периметр
Еще одна важная характеристика прямоугольника — периметр. Это сумма длин всех сторон. Периметр легко найти, измерив все стороны и сложив результаты. Но, как и в случае с площадью, лучше воспользоваться формулой. Сначала найдем периметр квадрата:
Р = АВ+ВС+СD+AD.
Но у квадрата все стороны одинаковые, значит, выражение можно записать иначе:
Р= АВ+АВ=АВ=АВ = 4 ∙ АВ, или 4АВ.
Для прямоугольника с разными сторонами периметр находится по такой же формуле:
Р = АВ+ВС+СD+AD.
Но здесь равны не все стороны, а только противоположные:
АВ= СD и ВС= AD
Перепишем начальную формулу по-другому:
Р= (АВ +СD) и (ВС + AD). Из равенства сторон получим Р=2АВ+2ВС + 2(АВ+ВС). Словами это будет звучать так:
Периметр прямоугольника равен сумме соседних сторон умноженной на два.
Как видно из приведенных утверждений, площадь и периметр прямоугольника можно вычислить двумя способами — непосредственным измерением и вычислением. Второй способ намного удобнее, особенно, если приходится находить площади и периметры реальных участков, например, площадки под строительство, дачного участка, комнаты.
Смотрите также другие геометрические фигуры:
Источник
Презентация к уроку математики 3 класс «Вычисление площади прямоугольника»
Описание презентации по отдельным слайдам:
«Площадь прямоугольника» 3 класс УМК «Перспективная начальная школа» Учитель начальных классов МКОУ «СОШ № 19» пос. Урожайный Предгорный район Ставропольский край Жажкова Марина Петровна
Цель: научить вычислять площадь прямоугольника Задачи: обучающие: вывести правило вычисления площади прямоугольника, знать термины «длина», «ширина»; уметь вычислять площадь прямоугольника; решать задачи разными способами; развивающие: развивать логическое мышление, воображение; развивать коммуникативные качества, речь; воспитывающие: воспитывать умение общаться; воспитывать устойчивый интерес к занятиям математикой. Планируемый результат Личностные умения: Проявлять: интерес к изучению темы; осознание собственных достижений при освоении учебной темы. Метапредметные умения: Познавательные умения: раскрывать значение понятий и использовать их в активном словаре; определять адекватную единицу измерения для вычисления площади и обосновывать свое мнение; определять порядок вычисления площади прямоугольника и обосновывать свое мнение. Регулятивные умения: выполнять учебное задание в соответствии с планом; выполнять учебное действие, используя алгоритм. Коммуникативные умения: адекватно использовать речевые средства для представления результата; использовать речь для регуляции своего действия. Предметные умения: Измерять и вычислять площадь геометрической фигуры; Переводить единицы измерения площади дм2 в см2, м2в дм2 и наоборот; Решать задачи на нахождение площади; Вычислять именованные числа.
Источник
Урок по математике на тему «Площадь прямоугольника» (3 класс УМК «Школа России»)
Конспект урока математики в 3 классе по теме:
УМК «Школа России»
Выполнила: учитель начальных классов
МБОУ «Пестречинская СОШ № 1»
2021- 2022 уч. год
Тема: Площадь прямоугольника
Тип урока: урок открытия нового знания
Цель урока: формировать представление о площади; познакомить учащихся с правилом нахождения площади прямоугольника и его использованием при решении несложных задач. формировать умение вычислять площадь прямоугольника по формуле.
• совершенствовать вычислительные умения,
• развивать навыки устного счета,
• пользоваться таблицей умножения и деления,
• актуализировать знания о геометрических фигурах и умение их
• способствовать развитию основных операций мышления (сравнение,
обобщение, умение делать выводы на основе полученной
• формировать навыки самоанализа,
• осуществлять пошаговый контроль своей деятельности,
• умение слушать других и принимать свою точку зрения.
• содействовать установлению в сознании ребенка устойчивых связей
между накопленным опытом и новым опытом познавательной и
• формирование основных компонентов УУД (умение ставить учебную
задачу, обобщать, делать выводы).
• развитие умения анализировать и находить пути решения проблемы.
• формировать навыки самоанализа,.
• совершенствовать вычислительные умения,
• развивать навыки устного счета,
• пользоваться таблицей умножения и деления,
• актуализировать знания о геометрических фигурах и умение их
• способствовать развитию основных операций мышления (сравнение,
обобщение, умение делать выводы на основе полученной
• формировать навыки самоанализа,
• осуществлять пошаговый контроль своей деятельности,
• умение слушать других и принимать свою точку зрения.
• содействовать установлению в сознании ребенка устойчивых связей
между накопленным опытом и новым опытом познавательной и
• формирование основных компонентов УУД (умение ставить учебную
задачу, обобщать, делать выводы).
• развитие умения анализировать и находить пути решения проблемы.
• формировать навыки самоанализа,.
• совершенствовать вычислительные умения,
• развивать навыки устного счета,
• пользоваться таблицей умножения и деления,
• актуализировать знания о геометрических фигурах и умение их
• способствовать развитию основных операций мышления (сравнение,
обобщение, умение делать выводы на основе полученной
• формировать навыки самоанализа,
• осуществлять пошаговый контроль своей деятельности,
• умение слушать других и принимать свою точку зрения.
• содействовать установлению в сознании ребенка устойчивых связей
между накопленным опытом и новым опытом познавательной и
• формирование основных компонентов УУД (умение ставить учебную
задачу, обобщать, делать выводы).
• развитие умения анализировать и находить пути решения проблемы.
• формировать навыки самоанализа,.
• совершенствовать вычислительные умения,
• развивать навыки устного счета,
• пользоваться таблицей умножения и деления,
• актуализировать знания о геометрических фигурах и умение их
• способствовать развитию основных операций мышления (сравнение,
обобщение, умение делать выводы на основе полученной
• формировать навыки самоанализа,
• осуществлять пошаговый контроль своей деятельности,
• умение слушать других и принимать свою точку зрения.
• содействовать установлению в сознании ребенка устойчивых связей
между накопленным опытом и новым опытом познавательной и
• формирование основных компонентов УУД (умение ставить учебную
задачу, обобщать, делать выводы).
• развитие умения анализировать и находить пути решения проблемы.
• формировать навыки самоанализа,.
• совершенствовать вычислительные умения,
• развивать навыки устного счета,
• пользоваться таблицей умножения и деления,
• актуализировать знания о геометрических фигурах и умение их
• способствовать развитию основных операций мышления (сравнение,
обобщение, умение делать выводы на основе полученной
• формировать навыки самоанализа,
• осуществлять пошаговый контроль своей деятельности,
• умение слушать других и принимать свою точку зрения.
• содействовать установлению в сознании ребенка устойчивых связей
между накопленным опытом и новым опытом познавательной и
• формирование основных компонентов УУД (умение ставить учебную
задачу, обобщать, делать выводы).
• развитие умения анализировать и находить пути решения проблемы.
• формировать навыки самоанализа,.
Вывести правило вычисления площади прямоугольника.
Актуализировать знания о признаках и свойствах геометрических фигур.
Способствовать совершенствованию вычислительных навыков.
Способствовать развитию основных операций мышления (сравнение, обобщение, умение делать выводы на основе полученной информации).
Развитие умения анализировать и находить пути решения поднимаемой проблемы.
Формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)
Формировать навыки самоанализа.
· Учебник М.И.Моро «Математика 3» (1 часть);
I Организационный момент: создание благоприятного психологического настроя к уроку.
II Актуализация знаний:
1. Делимое 49, делитель 7. Найдите частное.
2. Умножьте 6 на 4.
3. Сколько пятёрок в числе 30?
4. Во сколько число 32 больше 4?
5. Какое число меньше 18 в 6 раз?
Взаимопроверка в парах. Оценка соседу (смайлик на полях)
Устный счет (опрос таблицы умножения и деления по цепочке )
III Постановка учебной задачи:
— Ребята, определите по признакам, о какой фигуре идёт речь?
— фигура, у которой есть начало и конец (отрезок)
— фигура, состоящая из 3 углов (треугольник)
— фигура, у которой 4 угла и все стороны равны (квадрат)
— фигура, у которой все 4 угла прямые, а противоположные стороны равны (прямоугольник).
— Молодцы! Давайте вспомним нашу прошлую тему.
— Что такое площадь фигуры? (Место, которое эта фигура занимает)
— В каких единицах измеряется площадь фигуры? (В квадратных сантиметрах)
— Что такое квадратный сантиметр? (квадрат со стороной 1 см)
— Какие способы нахождения площади фигур мы изучили на прошлом уроке? (На глаз, способ наложения фигур друг на друга, считали, сколько квадратных сантиметров помещается в фигуре.)
— Попробуем найти площадь нашей доски, используя данные методы. Удобно ли нам будет измерять площадь таким способом? Почему?
— Какую цель мы поставим сегодня на уроке? (узнать более удобный способ нахождения площади прямоугольных предметов)
— Пожалуйста, сформулируйте тему нашего урока. (Площадь прямоугольника.)
IV Работа по теме урока.
— Рассмотрим прямоугольник на полях на с.60. Чему равна его длина? (4 см)
— Посмотрите, по длине в одном ряду укладывается 4 квадрата со стороной 1 см. Сколько таких рядов? (3)
— Мы можем посчитать квадраты и найти площадь этого прямоугольника. А есть еще один способ: можно число квадратов по ширине умножить на число рядов, т.е. 4*3=12.
— Как мы нашли площадь прямоугольника? (длину умножили на ширину)
— Давайте зафиксируем полученные знания.
— Правило в учебнике на стр.60.
Как измерить площадь?
Нет задачи проще!
Вот длина, вот ширина.
Чтобы площадь нам узнать,
Нужно их перемножать!
Физминутка «Мы – чертёжники!»
— Начертите глазами отрезок, кончиком носа – латинскую букву S, правой рукой – прямой угол, а левой – острый. Чертите аккуратно! Левой ногой – квадрат, а правой – прямоугольник.
V Первичное закрепление.
— Учебник: № 1 стр.60.
— Кто догадался, как найти площадь прямоугольника KMOA ?
— Найдите площадь прямоугольника DCNL ?
— Учебник: № 2 стр.60. Самостоятельное выполнение задания. Взаимопроверка.
— Учебник: № 3 стр.61.
— Скажите, как мы находим площадь прямоугольника?
Учащиеся еще раз проговаривают правило.
VI Самостоятельная работа по вариантам. 1 вариант чертит квадрат со стороной 2 см, 2 вариант чертит квадрат со стороной 3 см. Взаимопроверка.
— Карандашиком поставьте друг другу смайлики на полях.
— Ребята, какое правило мы узнали сегодня на уроке? (Как найти площадь прямоугольника.)
— Как найти площадь прямоугольника? (Надо длину умножить на ширину.)
VIII Домашнее задание.
— Большое спасибо всем за работу на уроке! Мне с вами было интересно!
Источник