- Как найти периметр трапеции
- Основные свойства трапеции
- Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
- Примеры решения задач
- Нахождение периметра трапеции: формула и задачи
- Формула вычисления периметра
- Примеры задач
- Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
- Принятые в формулах обозначения
- Найти периметр трапеции
- Основные свойства равнобедренной трапеции
- Формулы длин сторон равнобедренной трапеции:
- Формулы длины средней линии равнобедренной трапеции:
- Формулы определения длины высоты равнобедренной трапеции:
- В исходных данных: все стороны
- Периметр произвольной трапеции
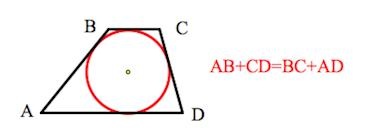
- Вписанная окружность
- Решение задач о прямоугольной трапеции
- Задача Даны три стороны, одна из которых перпендикулярная боковая.
- Задача Даны оба основания и угол при основании
- Свойства и признаки равнобедренной трапеции
- Формула определения радиуса вписанной в трапецию окружности
- Формулы определения длин отрезков проходящих через трапецию:
- Определение периметра прямоугольной трапеции
- Известны: диагонали и углы между ними
Как найти периметр трапеции
Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.
Периметр трапеции — это сумма длин всех его сторон.
Основные свойства трапеции
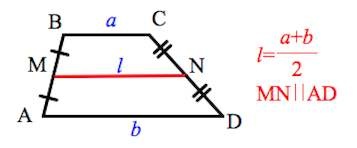
- средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;
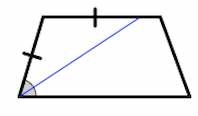
- биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;
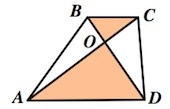
- треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;
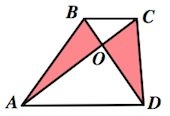
- треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;
- если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;
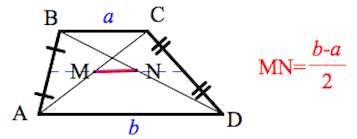
- точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;
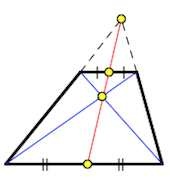
- середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;
Свойства равнобедренной трапеции
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
- диагонали равны;
- равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
- если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.
Способы нахождений периметра
Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.
По всем сторонам
Формула для нахождения периметра выглядит так:
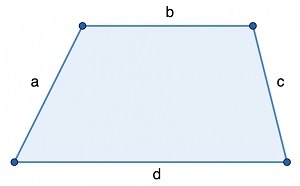
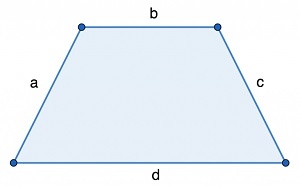
где a, b, c, d — стороны трапеции.
По сторонам равнобедренной трапеции
Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:
Через среднюю линию
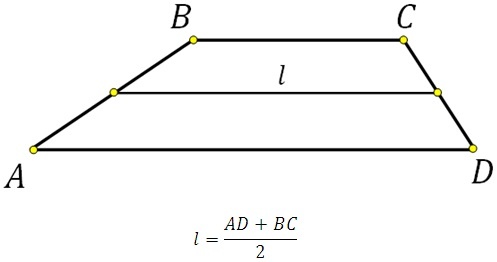
Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:
где l — средняя линия фигуры.
Примеры решения задач
Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.
Задача 1
Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.
Решение:
Нам пригодится самая первая формула для расчета:
Подставляем значения и получаем:
Задача 2
Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.
Решение:
Так как трапеция равнобедренная, удобнее всего будет использовать формулу:
Таким образом, получается:
\(P=2\times 7+5+8=27\) см.
Задача 3
Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.
Источник
Нахождение периметра трапеции: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) трапеции равняется сумме длин всех ее сторон.
P = a + b + c + d
- b и d – основания трапеции;
- a и с – ее боковые стороны.
Периметр равнобедренной трапеции
В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:
P = 2a + b + d или P = 2с + b + d
Периметр прямоугольной трапеции
Для расчета периметра используется такая же формула, что и для разносторонней трапеции.
P = a + b + c + d
Примеры задач
Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.
Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.
Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.
Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.
Источник
Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
Найти периметр трапеции

| a = |
| b = |
| c = |
| d = |
Вводить можно числа или дроби (-2.4, 5/7, …).
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| ( a + b ) sin α |
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с 2 – (((а – в) 2 + с 2 – d 2 )/(2(а – в))) 2 ). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с 2 – (а – в) 2 /4). Номер 2.
Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a , BC=b , CD=c , AD=d , имеет вид:
[ LARGE P_
где:
P – периметр трапеции
a, b, c, d – стороны трапеции
Вписанная окружность
Если в трапецию вписана окружность с радиусом 



Решение задач о прямоугольной трапеции
Прямоугольной называют трапецию, у которой углы при одной из боковых сторон равны 90 0 . Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.
Задача Даны три стороны, одна из которых перпендикулярная боковая.
Допустим, нам дана прямоугольная трапеция АВСД, у которой АВ перпендикулярно ВС. Известно, что АВ = 12 см, ВС = 1 см, АД = 6 см. Необходимо найти большую боковую сторону.
Из точки С опускаем проводим высоту СК и получаем прямоугольный треугольник СДК и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны СК = АВ = 12 см, а АК = ВС = 1 см.
Находим отрезок КД:
- КД = АД – АК = 6 – 1 = 5 (см)
Согласно теореме Пифагора:
- СД 2 =СК 2 +КД 2 =12 2 +5 2 =144+25=169
- СД = √169 = 13 (см)
Ответ: СД = 13 см
Задача Даны оба основания и угол при основании
Дана трапеция АВСД, у которой основания ВС и АД равны 6 и 10 см соответственно, угол ВАД – прямой, а СДА равен 45 градусов. Найдите меньшую боковую сторону.
- Проводим высоту СК и получаем прямоугольный треугольник СКД и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.
- КД = АД – АК = 10 – 6 = 4 см
- cos 45 = √2/2 = КД / СД, отсюда СД = КД / cos 45
- Получаем СД = 4/√2/2 = 4√2 (см)
Ответ: СД = 4√2 см
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Определение периметра прямоугольной трапеции
Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:
Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.
- опустим высоту из вершины С, высота CH = AB = 5см;
- исходя из рисунка 3, AH = BC = 7 см;
- HD = AD – AH = 10 – 7 = 3 см;
- далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
- подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.
Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:
- формула расчета длины основания через среднюю линию;
- формулы длин сторон через высоту и угол при нижнем основании трапеции;
- формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
- формулы длин сторон равнобедренной трапеции через площадь.
Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d1 2 * sin γ) / (а + в) или н = (d1 2 * sin δ) / (а + в). Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d1 2 * sin γ) / 2m или н = (d1 2 * sin δ) / 2m. Номер 6а.
Источник