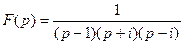Способы нахождения оригинала по изображению

Примеры решений задач по операционному исчислению (преобразованию Лапласа)

Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.

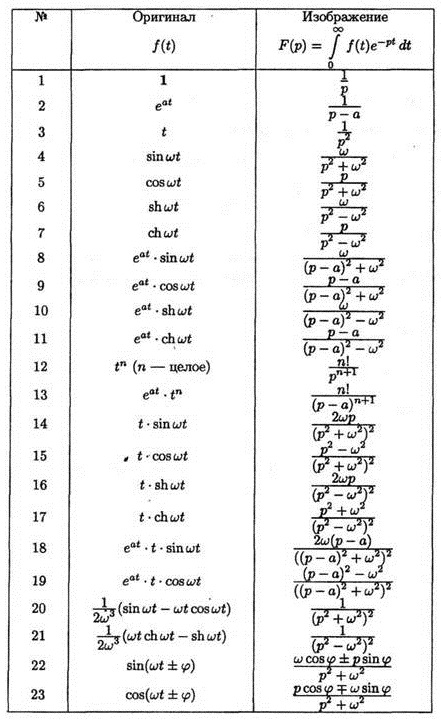
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:

$$F(p) = \int_0^\infty f(t) e^<-pt>dt$$

Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.

В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.

Как найти изображение функции

Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению

Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.

Задача 3. Найти изображение функции: $\int_0^t \cos \tau \cdot e^<-3\tau>d\tau. $

Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = \int_0^\infty f(x) e^<-px>dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).

Как найти оригинал функции

Задача 5. Найти оригинал изображения $F(p)$, где

Задача 6. Найти оригинал изображения

Задача 7. Найти оригинал для функции с помощью вычетов

Как решить ДУ (систему ДУ) операционным методом

Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом

Задача 9. Найти решение задачи Коши методами операционного исчисления

Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка

Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.

Задача 13. C помощью формулы Дюамеля найти решение уравнения

Задача 14. Решить систему ДУ с помощью преобразования Лапласа

Как решить интегральное уравнение

Задача 15. Методом операционного исчисления найти решение интегрального уравнения

$$ y(t)=\cos t +\int_0^t (t-\tau)^2 y(\tau)d \tau. $$

Задача 16. Решить интегральное уравнение

$$ \int_0^t ch (\tau) x(t-\tau)d \tau = t. $$

Как найти свертку функций

Задача 17. Найти свертку функций $f(t)=1$ и $\phi(t)=\sin 5t$.

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Источник

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Отыскание оригинала по изображению

Рассмотрим два способа для нахождения оригинала по заданному изображению:

Разложение $F(p)$ на сумму элементарных дробей и применение основных теорем операционного исчисления

Пример 3. Найти оригинал $f(t)$ для заданного изображения $F(p)$. \begin \begin F(p)&=\displaystyle\frac<1>=\displaystyle\frac<1>. \end \end Можно разложить на сумму элементарных дробей, а можно использовать теорему об интегрировании оригинала. Воспользуемся теоремой: \begin t\,e^<-t>\risingdotseq \frac<1>\,\, \Rightarrow \,\, \int\limits_0^t\tau\,e^<-\tau>\,d\tau\risingdotseq \frac<1>

. \end Вычислим интеграл и запишем оригинал $f(t)$: \begin \int\limits_0^t\tau\,e^<-\tau>\,d\tau = -(t+1)e^<-t>+1 \,\, \Rightarrow \,\, \end \begin \displaystyle\frac<1> \risingdotseq -(t+1)e^<-t>+1. \end

Пример 4. Найти оригинал $f(t)$ для заданного изображения $F(p)$. \begin F(p)=\displaystyle\frac>. \end Воспользуемся теоремой запаздывания. \begin \frac<1> \risingdotseq e^<-t>\,\, \Rightarrow \,\, \end \begin \frac>=\frac> \risingdotseq e^<-(t-1)>\cdot\eta(t-1). \end

Применение теорем разложения

Первая теорема разложения

Пусть $F(p)$ — аналитическая в окрестности $z=\infty$ функция и в этой окрестности раскладывается в ряд Лорана: \begin F(p)=\sum\limits_^<\infty>\displaystyle\frac. \end Тогда \begin F(p)\risingdotseq f(t)=\sum\limits_^<\infty>\displaystyle\frac<(k-1)!>t^. \end

Вторая теорема разложения

Пусть $F(p)$ — дробно-рациональная функция и $p_1, \ldots p_n$ — ее полюсы (простые или кратные). Тогда \begin F(p)\risingdotseq f(t)=\sum\limits_^\mbox\left(F(p_k)e^\right). \end

Пример 5. Найти оригинал $f(t)$ для заданного изображения $F(p)$. \begin F(p)=\displaystyle\frac

<(p+1)(p+2)(p+3)(p+4)>\end Обозначим $$H(p)=F(p)e^.$$ Все особые точки $H(p)$ — простые полюсы: $$p_1=-1,\,\, p_2=-2,\,\, p_3=-3,\,\, p_4=-4.$$ \begin \begin \mbox\left(H(p_1)\right)&=-\frac16e^<-t>, \\ \mbox\left(H(p_2)\right)&=e^<-2t>, \\ \mbox\left(H(p_3)\right)&=-\frac32e^<-3t>, \\ \mbox\left(H(p_4)\right)&=\frac23e^<-4t>. \end \end Тогда по второй теореме разложения получаем: \begin f(t)=-\frac16e^<-t>+e^<-2t>-\frac32e^<-3t>+\frac23e^<-4t>. \end

Пример 7. Найти оригинал $f(t)$ для заданного изображения $F(p)$. \begin F(p)=\displaystyle\frac <(p^2+1)^2>\end Обозначим $$H(p)=F(p)e^.$$ Особые точки $H(p)$ — полюсы второго порядка: $$p_1=i,\,\, p_2=-i.$$ \begin \begin \mbox\left(H(p_1\right))&=\frac(2+it)><4>, \\ \mbox\left(H(p_2\right))&=\frac(2-it)><4>. \end \end Тогда по второй теореме разложения: \begin f(t)=\frac14\left(2e^+2e^<-it>+i\,te^-i\,te^<-it>\right)=\mbox\,t-\frac12\,t\,\mbox\,t. \end

Пример 8. Найти оригинал $f(t)$ для заданного изображения $F(p)$.

Пример 9. Найти оригинал $f(t)$ для заданного изображения $F(p)$.

Источник

Оригинал и его изображение

Назначение . Данный сервис предназначен для нахождения онлайн оригинала f(t) по изображению F(p) . Результаты вычисления оформляются в формате Word (см. пример).

• Решение онлайн
• Видеоинструкция

Таблица оригиналов и изображений Лапласа

Изображение	Оригинал
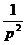	t
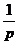	1
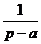	e at
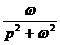	sin(ωt)
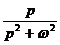	cos(ωt)
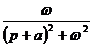	e -at sin(ωt)
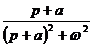	e -at cos(ωt)
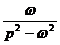	sh(ωt)
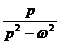	ch(ωt)

Начальной функцией или оригиналом называют функцию f(t) действительной переменной t , удовлетворяющей следующим условиям:

1. f(t)=0 при t 0 и s – некоторые вещественные числа, то |f(t)|≤Me st при t≥0.
2. f(t) — кусочно-непрерывная и интегрируемая на любом конечном отрезке изменения t .

Точная нижняя грань s₀ всех чисел s , для которых выполняется неравенство, называется показателем роста функции f(t) .

Теоремы запаздывания и смещения

Теорема смещения: L[e p₀t f(t)] = F(p-p₀).
Пример . (p+4)/((p+4) 2 +9) = e -4t cos(3t)

Источник

ВОССТАНОВЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ

Отображение, обратное к отображению Лапласа называется отображением Меллина

,

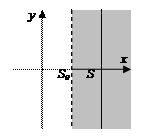
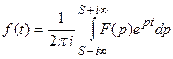
где интегрирование ведется по любой прямой Re p = S, S > S₀.

Непосредственное применение формулы обращения часто затруднительно и обычно пользуются теоремами разложения, являющимися следствиями из нее.

Первая теорема разложения. Если функция F(p) аналитична в окрестности бесконечно удаленной точки и ее разложение в ряд Лорана имеет вид

,

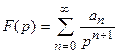
то оригиналом является функция

.

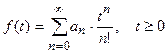
Вторая теорема разложения. Если F(p) имеет конечное число особых точек p₁ , p₂, . . . , p_n, то

.

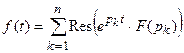
Во многих случаях оригинал легко восстанавливается по таблице изображений и свойствам преобразования Лапласа.

Пример 1. Найти оригинал для функции .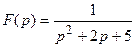

Преобразуем функцию, выделив в знаменателе полный квадрат.

.

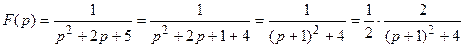
По таблице найдем оригинал

.

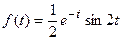
Пример 2.Найти оригинал для функции .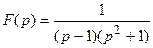

1 способ. Представим дробь в виде суммы простейших дробей

.

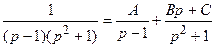
Вычислив неопределенные коэффициенты, получим

.

Для каждой дроби можно найти оригинал по таблице:

.

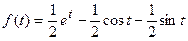
2 способ. Воспользуемся второй теоремой разложения.

Функция имеет три особые точки p₁ = 1, p₂ = i, p₃ = – i, являющиеся полюсами первого порядка. Найдем вычеты в этих точках для функции e pt F(p):

Res(e pt F(p), p₁) = ,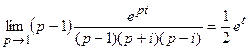

Res(e pt F(p), p₂) = ,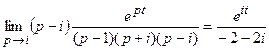

Res(e pt F(p), p₃) = .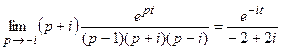

Оригинал является суммой вычетов:

.

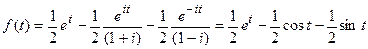
Пример 3.Найти оригинал для функции .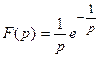

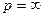
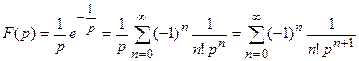
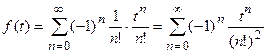
Воспользуемся первой теоремой разложения. Запишем ряд Лорана для функции F(p) в окрестности точки по известному разложению для экспоненты:

.

.

Источник