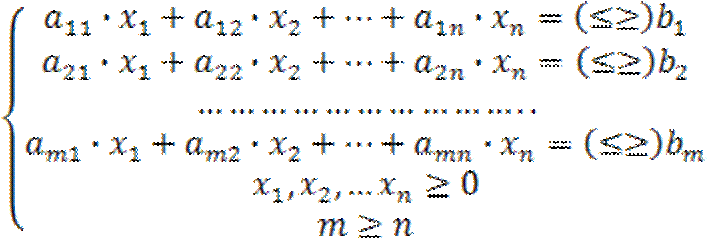Способы нахождения оптимальных решений

Оптимизационные модели в экономике. Способы нахождения оптимальных решений

Оптимизационные модели – это социально-экономические модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребленияи др.

Данные модели основаны на математическом аппарате теории программирования(«планирование»). Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Линейное программирование(ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие:

1) показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X = (x₁,x₂. x_n ). В качестве показателя оптимальности часто выступают экономические показатели: выручка, себестоимость, прибыль и пр.;

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Ограничения в экономических задачах могут быть по спросу, по запасам ресурсов, по трудоемкости, по затратам времени и пр.

Целевая функция (ЦФ)

Основные правилапостроение оптимизационной модели: число ограничений (m) должно быть больше либо равно числу искомых переменных x; в ограничения левая и правая части должны иметь одинаковые единицы измерения.

Допустимое решение– это совокупность чисел (план) X = (x₁, x₂, … x_n), удовлетворяющих ограничениям задачи. Оптимальное решение –это план, при котором ЦФ принимает свое максимальное (минимальное) значение.

В случае, если количество искомых величин х две, то удобно решение задачи представить в графической форме.

Каждое из неравенств задачи ЛП определяет на координатной плоскости (x₁,x₂) некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений(ОДР). ОДР всегда представляет собой выпуклуюфигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.

ЦФ L(X)= c₁x₁ + c₂x₂ при фиксированном значении L(X) = L определяет на плоскости прямую линию c₁x₁ + c₂x₂ = L . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня. Для нахождения оптимальной точки Х * =(х₁ * , х₂ * ) линии уровня путем параллельного переноса передвигаются вниз (если функция L стремиться к минимуму) или вверх (если функция L стремиться к максимуму).

Оптимальной считается точка, через которую проходит линия уровня Lmax (Lmin), соответствующая наибольшему (наименьшему) значению функции L(X). Оптимальное решение всегда находится на границе ОДР. При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

В случае, если количество искомых величин х более двух, то применяют метод перебора всех возможных вариантов с помощью ЭВМ (в Excel это надстройка «Поиск решения»).

На основе оптимизационных моделей были созданы различные вариации экономических задач:

— задача о размещении (транспортная задача)– это задача линейного программирования (ЛП), в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.Для решения транспортных задач применяются метод северо-западного угла и метод Фогеля.

— распределительная задача ЛП –это РЗ, в которой работы и ресурсы (исполнители) выражаются в различных единицах измерения. Типичным примером такой задачи является организация выпуска разнородной продукции на оборудовании различных типов.

Источник

Оптимизационные модели в экономике. Способы нахождения оптимальных решений

Оптимизационные модели – это социально-экономические модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребленияи др.

Данные модели основаны на математическом аппарате теории программирования(«планирование»). Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Линейное программирование(ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие:

1) показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X = (x₁,x₂. x_n ). В качестве показателя оптимальности часто выступают экономические показатели: выручка, себестоимость, прибыль и пр.;

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Ограничения в экономических задачах могут быть по спросу, по запасам ресурсов, по трудоемкости, по затратам времени и пр.

Целевая функция (ЦФ)

Основные правилапостроение оптимизационной модели: число ограничений (m) должно быть больше либо равно числу искомых переменных x; в ограничения левая и правая части должны иметь одинаковые единицы измерения.

Допустимое решение– это совокупность чисел (план) X = (x₁, x₂, … x_n), удовлетворяющих ограничениям задачи. Оптимальное решение –это план, при котором ЦФ принимает свое максимальное (минимальное) значение.

В случае, если количество искомых величин х две, то удобно решение задачи представить в графической форме.

Каждое из неравенств задачи ЛП определяет на координатной плоскости (x₁,x₂) некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений(ОДР). ОДР всегда представляет собой выпуклуюфигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.

ЦФ L(X)= c₁x₁ + c₂x₂ при фиксированном значении L(X) = L определяет на плоскости прямую линию c₁x₁ + c₂x₂ = L . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня. Для нахождения оптимальной точки Х * =(х₁ * , х₂ * ) линии уровня путем параллельного переноса передвигаются вниз (если функция L стремиться к минимуму) или вверх (если функция L стремиться к максимуму).

Оптимальной считается точка, через которую проходит линия уровня Lmax (Lmin), соответствующая наибольшему (наименьшему) значению функции L(X). Оптимальное решение всегда находится на границе ОДР. При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

В случае, если количество искомых величин х более двух, то применяют метод перебора всех возможных вариантов с помощью ЭВМ (в Excel это надстройка «Поиск решения»).

На основе оптимизационных моделей были созданы различные вариации экономических задач:

— задача о размещении (транспортная задача)– это задача линейного программирования (ЛП), в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.Для решения транспортных задач применяются метод северо-западного угла и метод Фогеля.

— распределительная задача ЛП –это РЗ, в которой работы и ресурсы (исполнители) выражаются в различных единицах измерения. Типичным примером такой задачи является организация выпуска разнородной продукции на оборудовании различных типов.

Источник

Методы принятия оптимальных решений

Вы будете перенаправлены на Автор24

Сущность понятия «оптимальное решение»

Оптимальное решение – это решение, которое по определенным критериям является наиболее подходящим в конкретной ситуации.

Сущность оптимального решения заключается в выборе наиболее предпочтительного варианта из всех существующих. Мерой предпочтения обычно выступает показатель качества.

Отличительной особенностью оптимального решения является его конкретика, то есть, подбор решения осуществляется согласно определенным критериям. Об оптимальности говорят тогда, когда присутствуют параметры выбора. Оптимальный вариант может быть таковыми при соблюдении одного фактора, но если на него будет влиять другой фактор, то он перестанет быть оптимальным.

Изучением проблемы оптимального выбора занимается теория принятия решения. Это прикладная область исследований, совмещающая в себе методы статистики, математики, психологии, менеджмента. Она занимается исследование закономерностей совершения выбора людьми при стремлении к достижению определенного результата. Теорию принятия решений делят на нормативную и дескрипитивную. Первая занимается теоретическим аспектом принятия рациональных решений. Вторая описывает практическую сторону принятия решений.

Экономические системы отличаются влиянием множества факторов. Кроме того, в них высокий уровень неопределенности, который усложняет принятие рационального решения. Обычно при планировании вырабатывается несколько альтернативных вариантов развития событий. Далее согласно приоритетным критериям выбираются наиболее подходящие варианты. Теория оптимальных решений позволяет максимально снизить будущую неопределенность среды.

Рационализация процесса принятия решений включает в себя поэтапное использование ситуационного анализа, определения проблемы и постановки цели, поиск и сбор необходимой информации, формирование альтернатив, разработка критериев и индикаторов, проведение оценки решений. На основе проведенный мероприятий корректируется план, а затем начинается процесс реализации. Последней стадией является оценка полученного результата.

Готовые работы на аналогичную тему

Неопределенность при принятии оптимальных решений

Главным параметром экономики является неопределенность. Неопределенность подразумевает, что результаты принимаемых решений не определены. Ее обычно делят на следующие категории:

• Стохастическая, при условии наличия информации о распределении вероятности решения на множество результатов.
• Поведенческая. Она проявляется тогда, когда есть информация о влиянии участников на результат.
• Природная. Присутствует информация о возможных результатах, между которыми отсутствует видимая связь.
• Априорная. Информации о возможных результатах нет.

Сущность принятия оптимального решения заключается в сужении вариантов решений для каждого из вышеперечисленных случаев, кроме априорного. Качество рекомендации может быть повышено при учете отдельных характеристик. Если рассматривается поведение индивида в экономике, то может учитываться его склонность к риску, отношение к собственным выигрышам и проигрышам. Обоснование решений проводится с помощью алгоритма адаптивного управления.

Теория принятия решений базируется на оптимальном выборе в условиях неопределенности. Сегодня он называется математическим ожиданием. Математическое ожидание является одним из ключевых понятий теории вероятности. Оно означает среднее значение случайной величины.

Интерес к поиску оптимальных решений возродился в конце тридцатых годов двадцатого века, когда возникла необходимость проверки статистических гипотез. Долгое время в экономике считалось, что поведение индивида является рациональным. То есть, субъект действует исходя из заданных экономических параметров, а не собственных желаний.

Поведенческая экономика является довольно молодой дисциплиной. Она сформировала теорию перспектив, которая показала, что результатом принятия решений человеком становится «потеря чувствительности к выигрышам».

Практическое применение методов принятия оптимальных решений

В экономике часто возникают задачи, которые требуют не просто найти решений, а выбрать наиболее выигрышный вариант. Такие задачи называют задачами оптимизации. В них выделяются два аспекта:

1. Наличие ограничений. Это факторы, которые устанавливают определенные лимиты на принятие решений.
2. Целевая функция. Это некоторое числовое значение, которое демонстрирует качество решения задачи.

Оптимальные решения принимаются с помощью математических инструментов вычисления. Выделяют несколько типов оптимизационных задач, под которые подбираются соответствующие параметры решения. Это производственная, транспортная задачи, задача об инвестициях, назначениях, а также задача коммивояжера и задача о ранце.

Производственные задачи возникают в работе предприятий при планировании ресурсов и нормы прибыли. Они позволяют выбрать виды продукции, а также оптимальное количество их выпуска для максимизации прибыли. Транспортные задачи решают вопросы грамотного и эффективного движения ресурсов или готовой продукции между несколькими объектами экономики. Перевозка считается оптимальной тогда, когда она получается наиболее экономичной. Инвестиционные задачи применяются на практике для определения наиболее подходящего объекта для вложений. Задачи о назначениях помогают подобрать наиболее подходящих исполнителей для выполнения определенных работ.

Методами оптимальных решений являются линейное и нелинейное программирование. Первые используют в своем инструментарии линейные функции или многочлены первой степени. В случае, если в задаче существуют ограничения, то решение осуществляется с помощью нелинейного программирования.

Таким образом, принятие оптимальных решений является одним из инструментов минимизации неопределенности в условиях экономических систем.

Источник