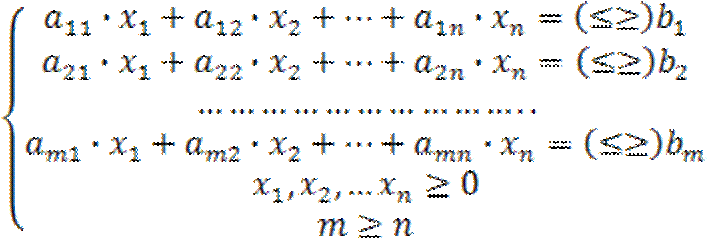Способы нахождения оптимального решения

Методы принятия оптимальных решений

Вы будете перенаправлены на Автор24

Сущность понятия «оптимальное решение»

Оптимальное решение – это решение, которое по определенным критериям является наиболее подходящим в конкретной ситуации.

Сущность оптимального решения заключается в выборе наиболее предпочтительного варианта из всех существующих. Мерой предпочтения обычно выступает показатель качества.

Отличительной особенностью оптимального решения является его конкретика, то есть, подбор решения осуществляется согласно определенным критериям. Об оптимальности говорят тогда, когда присутствуют параметры выбора. Оптимальный вариант может быть таковыми при соблюдении одного фактора, но если на него будет влиять другой фактор, то он перестанет быть оптимальным.

Изучением проблемы оптимального выбора занимается теория принятия решения. Это прикладная область исследований, совмещающая в себе методы статистики, математики, психологии, менеджмента. Она занимается исследование закономерностей совершения выбора людьми при стремлении к достижению определенного результата. Теорию принятия решений делят на нормативную и дескрипитивную. Первая занимается теоретическим аспектом принятия рациональных решений. Вторая описывает практическую сторону принятия решений.

Экономические системы отличаются влиянием множества факторов. Кроме того, в них высокий уровень неопределенности, который усложняет принятие рационального решения. Обычно при планировании вырабатывается несколько альтернативных вариантов развития событий. Далее согласно приоритетным критериям выбираются наиболее подходящие варианты. Теория оптимальных решений позволяет максимально снизить будущую неопределенность среды.

Рационализация процесса принятия решений включает в себя поэтапное использование ситуационного анализа, определения проблемы и постановки цели, поиск и сбор необходимой информации, формирование альтернатив, разработка критериев и индикаторов, проведение оценки решений. На основе проведенный мероприятий корректируется план, а затем начинается процесс реализации. Последней стадией является оценка полученного результата.

Готовые работы на аналогичную тему

Неопределенность при принятии оптимальных решений

Главным параметром экономики является неопределенность. Неопределенность подразумевает, что результаты принимаемых решений не определены. Ее обычно делят на следующие категории:

• Стохастическая, при условии наличия информации о распределении вероятности решения на множество результатов.
• Поведенческая. Она проявляется тогда, когда есть информация о влиянии участников на результат.
• Природная. Присутствует информация о возможных результатах, между которыми отсутствует видимая связь.
• Априорная. Информации о возможных результатах нет.

Сущность принятия оптимального решения заключается в сужении вариантов решений для каждого из вышеперечисленных случаев, кроме априорного. Качество рекомендации может быть повышено при учете отдельных характеристик. Если рассматривается поведение индивида в экономике, то может учитываться его склонность к риску, отношение к собственным выигрышам и проигрышам. Обоснование решений проводится с помощью алгоритма адаптивного управления.

Теория принятия решений базируется на оптимальном выборе в условиях неопределенности. Сегодня он называется математическим ожиданием. Математическое ожидание является одним из ключевых понятий теории вероятности. Оно означает среднее значение случайной величины.

Интерес к поиску оптимальных решений возродился в конце тридцатых годов двадцатого века, когда возникла необходимость проверки статистических гипотез. Долгое время в экономике считалось, что поведение индивида является рациональным. То есть, субъект действует исходя из заданных экономических параметров, а не собственных желаний.

Поведенческая экономика является довольно молодой дисциплиной. Она сформировала теорию перспектив, которая показала, что результатом принятия решений человеком становится «потеря чувствительности к выигрышам».

Практическое применение методов принятия оптимальных решений

В экономике часто возникают задачи, которые требуют не просто найти решений, а выбрать наиболее выигрышный вариант. Такие задачи называют задачами оптимизации. В них выделяются два аспекта:

1. Наличие ограничений. Это факторы, которые устанавливают определенные лимиты на принятие решений.
2. Целевая функция. Это некоторое числовое значение, которое демонстрирует качество решения задачи.

Оптимальные решения принимаются с помощью математических инструментов вычисления. Выделяют несколько типов оптимизационных задач, под которые подбираются соответствующие параметры решения. Это производственная, транспортная задачи, задача об инвестициях, назначениях, а также задача коммивояжера и задача о ранце.

Производственные задачи возникают в работе предприятий при планировании ресурсов и нормы прибыли. Они позволяют выбрать виды продукции, а также оптимальное количество их выпуска для максимизации прибыли. Транспортные задачи решают вопросы грамотного и эффективного движения ресурсов или готовой продукции между несколькими объектами экономики. Перевозка считается оптимальной тогда, когда она получается наиболее экономичной. Инвестиционные задачи применяются на практике для определения наиболее подходящего объекта для вложений. Задачи о назначениях помогают подобрать наиболее подходящих исполнителей для выполнения определенных работ.

Методами оптимальных решений являются линейное и нелинейное программирование. Первые используют в своем инструментарии линейные функции или многочлены первой степени. В случае, если в задаче существуют ограничения, то решение осуществляется с помощью нелинейного программирования.

Таким образом, принятие оптимальных решений является одним из инструментов минимизации неопределенности в условиях экономических систем.

Источник

Оптимизационные модели в экономике. Способы нахождения оптимальных решений

Оптимизационные модели – это социально-экономические модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребленияи др.

Данные модели основаны на математическом аппарате теории программирования(«планирование»). Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Линейное программирование(ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие:

1) показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X = (x₁,x₂. x_n ). В качестве показателя оптимальности часто выступают экономические показатели: выручка, себестоимость, прибыль и пр.;

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Ограничения в экономических задачах могут быть по спросу, по запасам ресурсов, по трудоемкости, по затратам времени и пр.

Целевая функция (ЦФ)

Основные правилапостроение оптимизационной модели: число ограничений (m) должно быть больше либо равно числу искомых переменных x; в ограничения левая и правая части должны иметь одинаковые единицы измерения.

Допустимое решение– это совокупность чисел (план) X = (x₁, x₂, … x_n), удовлетворяющих ограничениям задачи. Оптимальное решение –это план, при котором ЦФ принимает свое максимальное (минимальное) значение.

В случае, если количество искомых величин х две, то удобно решение задачи представить в графической форме.

Каждое из неравенств задачи ЛП определяет на координатной плоскости (x₁,x₂) некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений(ОДР). ОДР всегда представляет собой выпуклуюфигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.

ЦФ L(X)= c₁x₁ + c₂x₂ при фиксированном значении L(X) = L определяет на плоскости прямую линию c₁x₁ + c₂x₂ = L . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня. Для нахождения оптимальной точки Х * =(х₁ * , х₂ * ) линии уровня путем параллельного переноса передвигаются вниз (если функция L стремиться к минимуму) или вверх (если функция L стремиться к максимуму).

Оптимальной считается точка, через которую проходит линия уровня Lmax (Lmin), соответствующая наибольшему (наименьшему) значению функции L(X). Оптимальное решение всегда находится на границе ОДР. При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

В случае, если количество искомых величин х более двух, то применяют метод перебора всех возможных вариантов с помощью ЭВМ (в Excel это надстройка «Поиск решения»).

На основе оптимизационных моделей были созданы различные вариации экономических задач:

— задача о размещении (транспортная задача)– это задача линейного программирования (ЛП), в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.Для решения транспортных задач применяются метод северо-западного угла и метод Фогеля.

— распределительная задача ЛП –это РЗ, в которой работы и ресурсы (исполнители) выражаются в различных единицах измерения. Типичным примером такой задачи является организация выпуска разнородной продукции на оборудовании различных типов.

Источник

Как найти оптимальное решение производственного процесса

Управление производством предполагает постоянное принятие решений. Каждое принятое решение выбирается из определенного множества допустимых альтернатив. Задача менеджмента в данном случае состоит в том, чтобы выбрать оптимальное решение, то есть то решение, которое по определенным признакам предпочтительнее остальных. Решение будет считаться оптимальным, если оно приведет к максимально возможному положительному эффекту (например, росту прибыли предприятия).

Одним из методов, позволяющих найти оптимальное решение среди всего множества допустимых решений, является исследование операций. Исследование операций — один из разделов прикладной математики, суть которого заключается в поиске максимума (минимума) целевой функции, с учетом всех имеющихся ограничений. Суть экономики предприятия заключается в максимизации прибыли, с учетом ограниченности ресурсов, которыми располагает организация. Этим обусловлена применимость методов исследования операций в решении задач организации производственного процесса на предприятии. В экономике предприятия такие задачи называются задачами распределения ресурсов (или задачами оптимизации).

Рассмотрим пример, как можно применять методы исследования операций для решения производственных задач и как можно ускорить данный процесс путем применения встроенных возможностей MS Excel.

Предположим, автосервисное предприятие разработало для клиентов сезонные стимулирующие акции, суть которых заключается в том, что клиент, заплатив фиксированную сумму, получает целый пакет услуг по подготовке автомобиля к летнему сезону. Всего клиентам предложено два вида пакетов услуг:

1. пакет «Чистое стекло» стоимостью 3600 руб., в который входит комплекс работ по диагностике и осмотру автомобиля, очистка внутренней поверхности стекол автомобиля с применением специального спрея (плюс один флакон спрея в подарок); заливка в омывательный бачок стеклоочищающей жидкости (плюс одна бутыль стеклоочищающей жидкости в подарок);
2. 2) пакет «Свежий воздух» стоимостью 4300 руб., в который входит комплекс работ по диагностике и осмотру автомобиля, включая работы по очистке и дезинфекции кондиционера автомобиля с применением специального средства; очистка внутренней поверхности стекол автомобиля с применением специального спрея; заливка в омывательный бачок стеклоочищающей жидкости.

В табл. 1 представлен комплекс работ по диагностике и осмотру автомобиля (количество нормо-часов).

Таблица 1. Комплекс работ по диагностике и осмотру автомобиля (количество нормо-часов)

Работа

Пакет
«Чистое стекло»

Пакет
«Свежий воздух»

Проверка уровня моторного масла

Проверка уровня и плотности охлаждающей жидкости

Проверка уровня тормозной жидкости

Проверка состояния салонного фильтра

Визуальный контроль герметичности агрегатов

Визуальная проверка состояния тормозных дисков и колодок

Проверка тормозной системы на испытательном стенде

Корректировка давления в шинах

Функциональная проверка стеклоочистителей и стеклоомывателей

Проверка резиновых щеток стеклоочистителя на износ и наличие трещин

Проверка состояния радиатора охлаждения на предмет загрязнения

Проверка и корректировка фар

Проверка заряда аккумуляторной батареи

Короткий тест с помощью диагностической программы

Очистка и дезинфекция кондиционера

Итого

2,50

3,60

Таким образом, данные два пакета услуг отличаются друг от друга тем, что в первый пакет дополнительно входит подарок в виде одного флакона спрея для внутренней очистки стекол и одной бутыли стеклоочищающей жидкости, а во второй — проведение работ по очистке и дезинфекции кондиционера с применением специального средства.

Проведение сезонных акций позволяет предприятию решить целый ряд задач:

1. 1. Привлечение клиентов.
2. 2. Сбыт залежавшихся сезонных товаров (автохимия).
3. 3. Загрузка механиков.
4. 4. Получение дополнительной прибыли.
5. По задумке менеджмента организации, количество пакетов ограничено:

• во-первых, акция будет продолжаться до тех пор, пока не кончатся складские остатки участвующей в акции автохимии;
• во-вторых, срок проведения акции органичен одним месяцем (апрелем);
• в-третьих, на выполнение сервисных мероприятий могут быть задействованы только четыре механика.

Таким образом, ресурсы, выделяемые на проведение данной акции, ограничены. Ограничения по ресурсам на проведение сезонной акции представлены в табл. 2.

Таблица 2. Ограничения по ресурсам на проведение сезонной акции

Задействованные ресурсы

Расход ресурсов

Запас ресурсов

пакет«Чистое стекло»

пакет«Свежий воздух»

Работа механика, ч

Спрей для очистки внутренней поверхности стекла, уп.

Стеклоомывающая жидкость, уп.

Жидкость для очистки и дезинфекции кондиционера, уп.

На проведение сезонной акции может быть выделено не более:

• 320 флаконов спрея для очистки внутренней поверхности стекла;
• 260 бутылей стеклоомывающей жидкости;
• 150 бутылей жидкости для очистки и дезинфекции кондиционера.

К тому же ограничено время работы механиков: в апреле 22 рабочих дня, продуктивный рабочий день механика — 7 ч в день. Следовательно, располагаемый фонд рабочего времени четырех механиков равен 616 ч (4 x 22 x 7).

Всего на один пакет «Чистое стекло» необходимо затратить:

• 2,5 ч работы механика;
• 2 флакона спрея для очистки внутренней поверхности стекла (один использовать, один — в подарок);
• 2 бутыли стеклоомывающей жидкости (одну использовать, одну — в подарок).

На пакет «Свежий воздух» необходимо затратить:

• 3,6 ч работы механика;
• 1 флакон спрея для очистки внутренней поверхности стекла;
• 1 бутыль стеклоомывающей жидкости и одну бутыль жидкости для очистки и дезинфекции кондиционера.

Ограничение по ресурсам является одним из условий задачи исследования операций. Характерной особенностью исследования операций является системный подход. В связи с этим существующие ограничения по ресурсам можно представить в виде системы уравнений. Для начала введем обозначения для переменных нашей задачи:

• X1 — количество пакетов «Чистое стекло»;
• Х2 — количество пакетов «Свежий воздух»;
• A — количество часов механика;
• B — количество флаконов спрея для внутренней очистки стекол;
• C — количество бутылей стеклоомывающей жидкости;
• D — количество бутылей жидкости для очистки и дезинфекции кондиционеров.

Далее нужно определиться с ограничениями, которым должны удовлетворять переменные нашей задачи:

1) во-первых, количество пакетов не может быть отрицательным: Х1, Х2 ≥ 0;

2) во-вторых, расход ресурсов не должен превышать имеющиеся запасы. Это можно выразить при помощи неравенств:

• по ресурсу А: 2,5 x Х1 + 3,6 x Х2 ≤ 616;
• по ресурсу В: 2 x Х1 + 1 x Х2 ≤ 320;
• по ресурсу С: 2 x Х1 + 1 x Х2 ≤ 260;
• по ресурсу D: 0 x Х1 + 1 x Х2 ≤ 150.

Затем следует определиться с целевой функцией (направлением для оптимизации). Логично было бы распределить квоту на оказание пакетов услуг таким образом, чтобы предприятие получило максимальную прибыль. Для этого нужно рассчитать, сколько прибыли приносит продажа одного пакета услуг, то есть сопоставить цену реализации пакета и стоимость затрачиваемых ресурсов. Как уже говорилось выше, стоимость пакета «Чистое стекло» составляет 3600 руб., а пакета «Свежий воздух» — 4300 руб. Данные суммы необходимо сопоставить с затратами на выполнение услуг:

• тарифная часовая ставка механика составляет 350 руб. за нормо-час (включая налоги и взносы с ФОТ);
• стоимость флакона жидкости для очистки внутренней поверхности стекла — 661 руб.;
• стоимость бутыли стеклоочищающей жидкости — 250 руб.;
• стоимость бутыли жидкости для очистки и дезинфекции кондиционеров — 1589 руб.

Расчет прибыли от реализации каждого из пакетов на основании имеющихся данных представлен в табл. 3.

Таблица 3. Прибыль от реализации пакетов услуг, руб.

Ресурс

Цена ресурса

Пакет«Чистое стекло»

Пакет«Свежий воздух»

Затраты на оплату труда механика

Затраты на спрей для очистки стекол

Затраты на стеклоомывающую жидкость

Затраты на жидкость для очистки и дезинфекции кондиционера

Итого затраты на пакет

2697,00

3760,00

Стоимость пакета

3600,00

4300,00

Прибыль от продажи пакета

903,00

540,00

Итак, продажа одного пакета «Чистое стекло» принесет предприятию 903 руб. прибыли, а пакета «Свежий воздух» — 540 руб.

Целевая функция (Z) в данном случае примет вид:

Задача — найти максимум целевой функции с учетом существующих ограничений:

Решим эту задачу, используя симплекс-метод. Симплекс-метод представляет собой алгоритм решения оптимизационной задачи линейного программирования путем перебора вершин выпуклого многогранника в многомерном пространстве. Дело в том, что представленная система уравнений имеет бесконечное множество решений. Если представить это множество графически, то получится многогранник, в одной из вершин которого находится оптимальное решение. Симплекс-метод как раз и заключается в нахождении исходной вершины множества допустимых решений, в последовательном переходе от одной вершины к другой, ведущий к оптимизации значения целевой функции.

Для решения нашей задачи симплекс-методом ее нужно привести к так называемому стандартному виду: преобразовать неравенства нашей системы ограничений в равенства, добавив в левую часть каждого из уравнений неотрицательные числа (назовем их Х3, Х4, Х5 и Х6), которые называются балансовыми переменными (переменные Х1 и Х2 называются свободными). Получится следующая система уравнений:

Решить поставленную задачу симплекс-методом удобнее всего с помощью симплекс-таблицы. Этапы поиска оптимального решения следующие:

• построение первой симплекс-таблицы;
• последовательное преобразование симплекс-таблиц по определенному алгоритму, до выполнения определенных условий.

Последовательное преобразование симплекс-таблиц и будет означать переход из одной точки множества допустимых решений в другую, до тех пор, пока не будет найдено оптимальное решение. Прежде чем составить первую симплекс-таблицу, необходимо преобразовать целевую функцию в следующий вид:

Теперь строим первую симплекс-таблицу. Столбцами будут переменные Х1–Х6, а строками — имеющиеся ресурсы (А, В, С, D). На пересечении строки и столбца находятся коэффициенты перед переменными по каждому виду ресурса в нашей системе ограничений. Так, по строке А (время работы механиков) в столбце Х1 будет стоять коэффициент 2,5; в столбце Х2 — 3,6; в столбце Х3 — 1, а в Х4–Х6 — 0.

Также вводится дополнительный столбец (назовем его b), в котором стоят ограничения по каждому из ресурсов. После этого вводится дополнительная строка Е, в которой содержатся коэффициенты в нашей целевой функции (Z – 903 x Х1 – 540 x Х2 = 0). Получилась следующая симплекс-таблица, представленная в табл. 4.

Таблица 4. Первая симплекс-таблица

Ресурс

2,5

2

2

1

0

0

1

0

260

0

–903

Значение функции Z равно числу, стоящему в правом нижнем углу табл. 4. Последующее преобразование симплекс-таблицы связано с выбором разрешающей строки и разрешающего столбца.

Разрешающим столбцом является тот столбец, у которого коэффициенты в целевой функции (строка Е) являются отрицательными и наибольшими по модулю. В данной таблице это будет столбец Х1, у которого по строке Е стоит значение –903. Следует заметить, что преобразование симплекс-таблиц будет происходить до тех пор, пока в строке Е не останется отрицательных значений.

Теперь нужно найти разрешающую строку. Она определяется путем нахождения минимального отношения коэффициентов в столбце b к соответствующим коэффициентам разрешающего столбца (за исключением нулевых и отрицательных элементов, по которым соотношение не определяется).

Для нашей первой симплекс-таблицы разрешающей будет строка С, так как именно в ней наименьшее соотношение элемента столбца b и элемента разрешающего столбца Х1 (260 / 2 = 130). Элемент таблицы, который находится на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом (в табл. 4 ячейка данного элемента выделена цветом).

После нахождения разрешающего элемента производится процедура симплекс-преобразования. Цель данной процедуры — сделать разрешающий элемент равным единице, а все остальные элементы разрешающего столбца — нулевыми.

Преобразование осуществляется определенными методами:

• разрешающую строку можно делить и умножать на любое число;
• к любой строке можно прибавлять или отнимать соответствующие элементы разрешающей строки, поделенные или умноженные на любое число.

Выполним предложенные преобразования. Чтобы приравнять разрешающий элемент к единице, разделим все элементы разрешающей строки на 2. Затем из элементов строки А отнимем элементы разрешающей строки С, умноженные на 2,5. Далее из элементов строки В отнимем элементы разрешающей строки С, умноженные на 2. Со строкой D никаких преобразований не производим (в разрешающем столбце итак стоит нулевое значение). К элементам строки Е прибавляем элементы разрешающей строки С, умноженные на 903. Получилась вторая симплекс-таблица, которая представлена в табл. 5.

Таблица 5. Вторая симплекс-таблица

Ресурс

0

2,35

1

0

–1,25

0

291

0

0,5

1

–88,5

Повторяем ту же процедуру, что и с табл. 4. Для начала находим разрешающий столбец (с наибольшим по модулю отрицательным коэффициентом перед целевой функцией). Разрешающим в данном случае будет столбец Х2. Далее находим разрешающую строку. Это будет строка А, так как для нее выполняется условие минимальности соотношения элемента столбца b к соответствующему элементу разрешающего столбца Х2 (291 / 2,35 = 123,83).

Элемент на пересечении строки А и столбца Х2 будет разрешающим. Выполняем преобразование разрешающего элемента в единицу, а остальных элементов столбца Х2 в нули. Все элементы строки А делим на 2,35. Со строкой В никаких преобразований не производим (в разрешающем столбце и так стоит нулевое значение). Из элементов строки С отнимем элементы разрешающей строки А, умноженные на 0,5 и деленные на 2,35. Из элементов строки D отнимем элементы разрешающей строки А, деленные на 2,35. К элементам строки Е прибавляем элементы разрешающей строки А, умноженные на 88,5 и деленные на 2,35. Получилась третья симплекс-таблица, которая представлена в табл. 6.

Таблица 6. Третья симплекс-таблица

Ресурс

В полученной симплекс-таблице в строке Е, содержащей коэффициенты целевой функции, нет отрицательных значений, следовательно вычисление завершено. Значения переменных Х1 и Х2 расположены в столбце b на тех строках, в которых в столбцах Х1 и Х2 стоят единицы. Соответственно, Х1 = 68,0851, а Х2 = 123,8298. Значение целевой функции при таких переменных будет равно:

Z = 903 x 68,0851 + 540 x 123,8298 = 128 348,94.

Полученная сумма — это максимальная прибыль предприятия от продажи пакетов. Однако следует заметить, что при решении поставленной задачи не была учтена одна существенная оговорка. Дело в том, что количество проданных сезонных пакетов может быть лишь целым числом (автосервис не может продать часть пакета услуг).

Существует ряд приемов, которые позволяют вводить в задачу оптимизации условие целочисленности переменных за счет ввода дополнительных ограничений системы. Однако современному специалисту проще решать данную задачу, используя инструмент MS Excel — «Поиск решения», который позволяет не только находить оптимальное решение задачи, но и делать его таковым, чтобы оно удовлетворяло условию целочисленности переменных.

Покажем это на наглядном примере. Для начала следует ввести все данные задачи в рабочий лист MS Excel (рис. 1).

Рис. 1. Ввод данных задачи оптимизации в MS Excel

Сначала следует ввести нормативы расхода имеющихся ресурсов на каждый из пакетов:

• в ячейки B3:B6 вводятся нормативы расхода всех ресурсов на продажу одного пакета «Чистое стекло»;
• в ячейки C3:C6 вводятся нормативы расхода всех ресурсов на продажу одного пакета «Свежий воздух»;
• в ячейки D3:D6 заносят запасы (лимиты расхода) по каждому из ресурсов.

Для того чтобы посчитать общий расход ресурсов и соотнести его с запасами, необходимо ввести данные о количестве проданных пакетов (ячейки В16 и С16). Для начала проставим там единичные значения (как будто продано по одному сезонному пакету). Общий расход ресурсов рассчитывается в диапазоне ячеек A8:D13, в котором количество проданных пакетов (ячейки В16 и С16) умножается на норматив расхода (диапазоны B3:B6 и C3:C6). В диапазоне D10:D13 рассчитывается суммарный расход по каждому из ресурсов.

Так, например, расход нормо-часов механиков по пакету «Чистое стекло» производится в ячейке В10 путем умножения значений ячейки В16 (количество проданных пакетов «Чистое стекло») на ячейку В3 (норматив выполнения работ по пакету «Чистое стекло»). Расход нормо-часов механиков по пакету «Свежий воздух» производится в ячейке С10 путем умножения значений ячейки С16 (количество проданных пакетов «Свежий воздух») на ячейку С3 (норматив выполнения работ по пакету «Свежий воздух»).

Итоговое значение расхода часов механиков рассчитывается в ячейке D10 путем сложения значений ячеек В10 и С10 (сумма в ячейке D10 не должна превышать лимит, установленный в ячейке D3).

Также на рабочем листе идет расчет прибыли от продажи пакетов (ячейки В18 и С18). Для этого размер прибыли от продажи одного пакета (значения проставлены в ячейках В17 и С17) умножается на количество проданных пакетов (ячейки В16 и С16). В ячейке D18 стоит итоговое значение прибыли.

Цель — максимизировать значение, рассчитываемое в ячейке D18 при соблюдении всех ограничений задачи.

Воспользуемся инструментом «Поиск решения» (находим в меню «Данные» — «Анализ»). Диалоговое окно представлено на рис. 2.

Рис. 2. Диалоговое окно инструмента «Поиск решения»

По условиям поставленной задачи необходимо установить в целевую ячейку D18 (общая прибыль от продажи пакетов) максимальное значение, изменяя ячейки В16:С16 (количество проданных пакетов «Чистое стекло» и «Свежий воздух»).

При этом должны быть прописаны все ограничения нашей задачи:

• В16 и С16 >= 0 (количество проданных пакетов неотрицательно);
• D10

Источник